本文为原创文章，未经本人允许，禁止转载。转载请注明出处。
1.图像分割的概念
根据灰度、颜色、纹理和形状等特征把图像划分成若干互不交迭的区域，并使这些特征在同一区域内呈现出相似性，而在不同区域间呈现出明显的差异性。
2.主要的图像分割算法
- 基于阈值的分割方法
- 基于边缘的分割方法
- 基于区域的分割方法
- 基于特定理论的分割方法
3.Graph Cut图割算法
Graph Cut算法是由Yuri Y.Boykov和Marie-Pierre Jolly于2001年提出的一种基于图论的图割算法。原论文：Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images.。
Graph Cut的目标是通过人工交互式分割技术，将图像分割成两个部分：前景(object,简写为obj)和背景(background,简写为bkg)。
所谓人工交互式是指事先需要人为的标注一部分肯定属于前景或背景的像素点（称为seeds），作为先验信息。如下图所示，白色区域为事先标注的属于前景的像素点集合，红色区域为事先标注的属于背景的像素点集合。
3.1.基础知识储备
首先，我们先来了解一些关于图论的基础知识。
一张图其实就是许多像素点p的集合，我们把这个集合称为P，其中$p \in obj$或者$p \in bkg$，并且有$p \in P$。每两个相邻的像素点都会产生一个无序像素点对$\lbrace p,q \rbrace$，我们把这些无序像素点对形成的集合称为N。例如，在二维图像中，一个像素点有8个邻居节点，在三维图像中，一个像素点有26个邻居节点。
假设有一个二值(只能是0或1)的vector，$A=(A_1,…,A_p,…,A_{|P|})$。其中，$A_p$是该像素点的label，只能是obj或者bkg。那么我们就可以通过A来定义任意一种分割方法。
3.2.构建惩罚函数（cost function）
我们通过构建一个惩罚函数来计算任意分割A的代价（cost），代价最小的分割方法即为Graph Cut分割的最后结果。
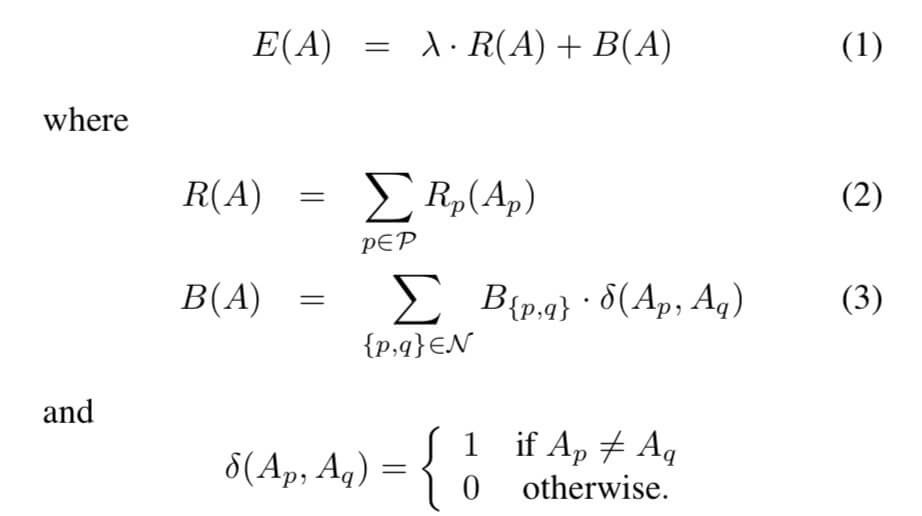由式（1）可知，惩罚函数$E(A)$主要分为两项：
- 区域项（region properties）$R(A)$：等于分割A中每一个像素点的cost总和。单个像素点p的cost为$R_p(A_p)$，因为$A_p$只有两种取值，所以又等同于$R_p(obj)$或$R_p(bkg)$，即像素点p被归为obj的cost或者被归为bkg的cost。且有$\lambda \ge 0$，其中，系数$\lambda$主要用于调节区域项和边界项的比例关系。
- 边界项（boundary properties）$B(A)$：是被分割开的边的cost总和，简单理解就是将这些边割开所要付出的代价。每一对相邻像素$\lbrace p,q \rbrace$所连接成的边的cost是$B_{\lbrace p,q \rbrace}$。当p和q的差异（比如距离上的差异或者像素值上的差异）很小时，$B_{\lbrace p,q \rbrace}$很大。当p和q的差异很大时，$B_{\lbrace p,q \rbrace}$很小。$\delta (A_p,A_q)$主要确保是将不同标签的像素点分开时才计算该边的cost，因为在进行图像分割的时候，割开的肯定是具有不同标签的像素对所连成的边。
接下来我们一步步来看cost function中每一项具体是怎么计算的。
3.2.1.Graph Cut有关术语
我们可以将一幅图像理解为一个无向图$G=<V,E>$，其中，V是像素点的集合，E是无向边的集合。如下图所示：
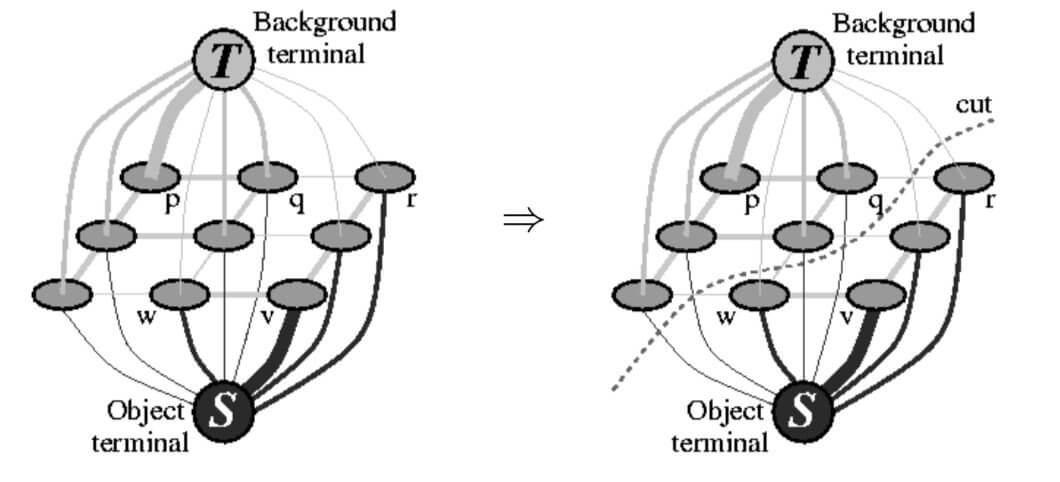该图是一幅3*3分辨率的图像，共有9个像素点。但是我们可以看到图中多了两个特殊点，称为终端节点（terminals）。这两个终端节点分别为前景节点（object terminal，即S点）和背景节点（background terminal，即T点）。同样的，我们将边也分为两种，像素点之间相连接的边为n-link，像素点与终端节点相连的边为t-link。其实，联系之前3.2部分讲的，t-link的cost就是$R_p(A_p)$，n-link的cost就是$B_{\lbrace p,q \rbrace}$。
当进行分割时，分割路径上的n-link断开，属于前景的像素点与T点连接的t-link断开，相反的，属于背景的像素点与S点连接的t-link断开，图像就自然而然的被分成了两部分。这种分割方法的cost就可以套用之前提到的惩罚函数进行计算了。最后计算所有可能的分割方式，得到cost最小的分割方式（最小割），即等同于求惩罚函数的最小值。那么怎么快速求出惩罚函数的最小值呢，该篇论文的作者提出了一种新的最大流-最小割的算法来解决这个问题（关于最大流-最小割算法的相关内容请移步本人另一篇博客👉【图像分割】“最大流-最小割”算法）。
3.2.2.区域项的计算
区域项的计算需要用到前文中提到的人工标注的seeds，分别按照前景seeds和背景seeds绘制两个灰度直方图。
直方图大家都很熟悉，那么什么是灰度直方图呢？其实很简单，将原始的图像先进行转化，得到灰度图像。灰度图像的像素值一般在0～255之间，这也就是直方图的横轴，而直方图的纵轴就是等于各个灰度值的像素点的个数。
现在，假设有像素点p（非seeds），其像素值为$I_p$，根据直方图，可以得到该像素点属于前景的概率为$Pr(I_p|O)$，即在前景灰度直方图中，像素值为$I_p$的像素点数目除以该直方图所有像素点的数目。同理，可以求得点p属于背景的概率为$Pr(I_p|B)$。对其取负对数，即可得到$R_p(A_p)$的计算公式：
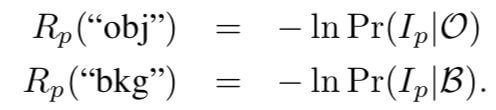
3.2.3.边界项的计算
边界项的计算很简单，直接上公式：
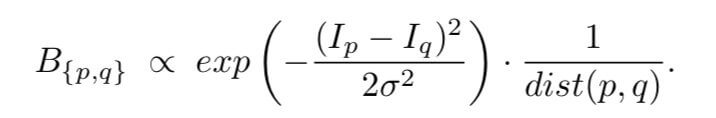$\propto$是成正比的意思。公式右边主要分为两部分：
- 第一部分主要衡量两个相邻像素点的像素值差异，是一个高斯分布，$I_p$和$I_q$是$\lbrace p,q \rbrace$中p,q的灰度值，$\sigma^2$是方差。
- 第二部分主要衡量两个相邻像素点的距离差异，其中，$dist(p,q)$指的是p,q之间的距离，常采用欧式距离进行计算。
