本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.导数
1.1.导数的定义
当函数$y=f(x)$的自变量$x$在一点$x_0$上产生一个增量$\Delta x$时,函数输出值的增量$\Delta y$与自变量增量$\Delta x$的比值在$\Delta x$趋于$0$时的极限$a$如果存在,$a$即为在$x_0$处的导数,记作$f’(x_0)$或$\frac{df(x_0)}{dx_0}$。
即$f’(x_0)=lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$
个人理解:
导数的计算方式类似于三角函数中的$tan$,即该点切线的斜率,反应曲线变化的快慢。
👉导数是对函数进行线性逼近。
这么说的原因可以参照函数导数的一个等价定义:
如果存在一个实数$L$,使得$f(x)$满足,
\[f(x)=f(x_0)+L(x-x_0)+o(x-x_0),x\to x_0\]那么$f(x)$在$x_0$处可导且导数$f’(x_0)=L$。
从上式可以很容易的看出,导数是对函数进行的线性逼近,而导数的值就是直线的斜率。
1.1.1.连续与可导
函数$y=\mid x\mid$的图像见下:

函数在原点处虽然连续但是不可导,无法进行线性逼近。因此连续和可导有如下关系:
- 连续不一定可导
- 可导一定连续
那么如何对上述函数进行逼近呢?答:可以左右两边各做一次逼近。
1.2.高阶导数
\[f^{(n)}(x)=\frac{d}{dx}f^{(n-1)}(x)\]高阶导数的应用:可用二阶导数判断函数为凸函数或者为凹函数。
$f(x)$在区间[a,b]上连续,在(a,b)内二阶可导,那么:
- $f’^\prime(x)\geqslant 0$时为凸函数($f’^\prime(x)>0$时称为严格凸函数)
- $f’^\prime(x)\leqslant 0$时为凹函数($f’^\prime(x)< 0$时称为严格凹函数)

凸函数和凹函数的定义国内外可能会有所不同。有的也将第一条曲线称为凹函数,第二条曲线称为凸函数。
若函数为凸函数:
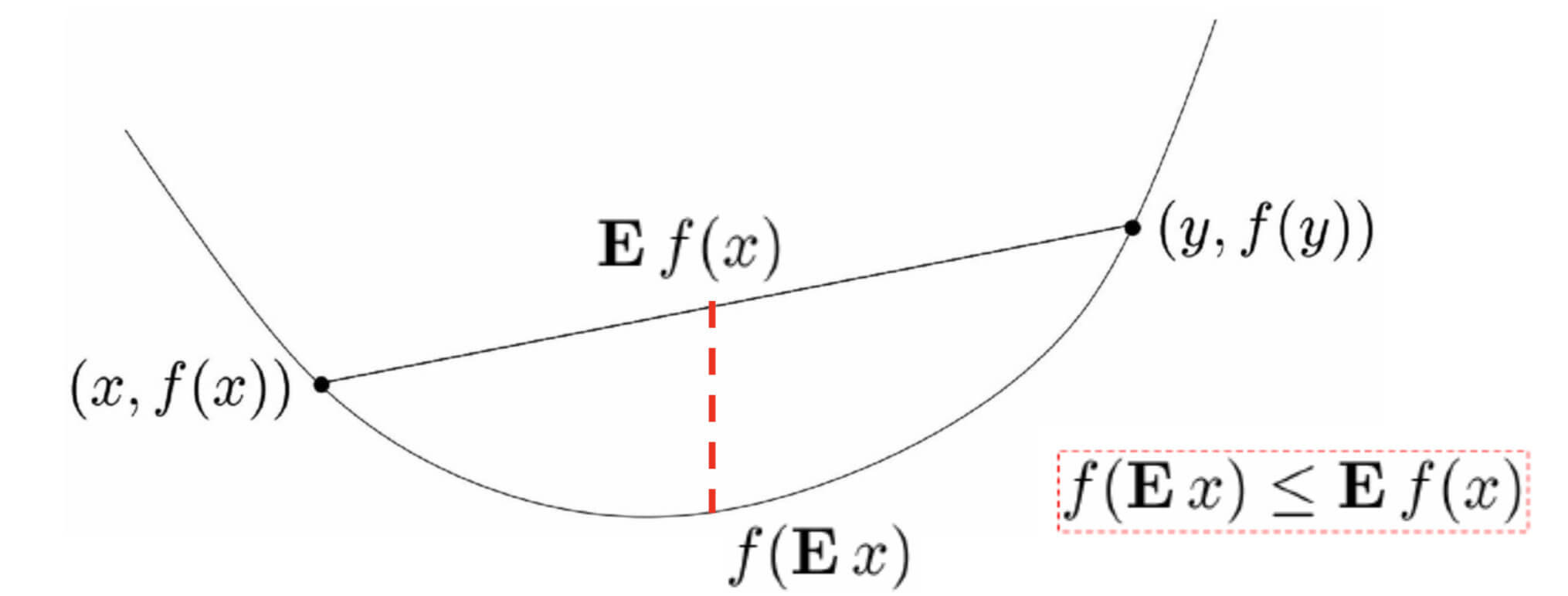
则有:$f(\theta x +(1-\theta)y)\leqslant \theta f(x)+(1-\theta)f(y)$。其中,$\theta x+(1-\theta)y$代表在$x,y$范围内的任意一个值;$\theta f(x)+(1-\theta)f(y)$代表在$f(x),f(y)$范围内的任意一个值。
进一步推广可以得到琴生不等式:$f(Ex)\leqslant Ef(x)$,($f$为凸函数,$E$为期望)。该式也可写为:$f(\theta_1 x_1+\theta_2 x_2+…+\theta_n x_n)\leqslant \theta_1 f(x_1)+\theta_2 f(x_2)+…+\theta_n f(x_n),0\leqslant \theta_i\leqslant1,\theta_1+\theta_2+…+\theta_n=1$。
❗️琴生不等式和凸函数互为充要条件。
1.3.求导法则
👉求导四则运算法则与性质:
若函数$u(x),v(x)$都可导,则
- $(u(x)\pm v(x))’=u’(x)\pm v’(x)$
- $(u(x)\bullet v(x))’=u’(x)\bullet v(x)+u(x)\bullet v’(x)$
- $(\frac{u(x)}{v(x)})’=\frac{u’(x)v(x)-v’(x)u(x)}{v^2(x)}$
👉复合函数求导法则(链式法则):
- $\frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}$
👉反函数求导:
- $\frac{d}{dx}(f^{-1})=\frac{1}{\frac{d}{dx}(f)}$
即:反函数的导数等于原函数导数的倒数。
反函数:
一般地,设函数$y=f(x)(x\in A)$的值域是$C$,若找得到一个函数$g(y)$在每一处$g(y)$都等于$x$,这样的函数$x=g(y)(y\in C)$叫做函数$y=f(x)(x\in A)$的反函数。
原函数为$y=f(x)$,对应的反函数记为$x=f(y)$或$y=f^{-1}(x)$
简单的说就是$x,y$互换位置,例如:
原函数为$y=2x-1$,反函数为$y=0.5x+0.5$
原函数为$y=2^x$,反函数为$y=log_2x$
1.4.常用函数的导数
| $C’=0$ | $x’=1$ | $(x^n)’=nx^{n-1}$ |
|---|---|---|
| $(\sin x)’=\cos x$ | $(\cos x)’=-\sin x$ | $(a^x)’=a^x\ln a$ |
| $(e^x)’=e^x$ | $(\log _a x)’=\frac{1}{x}\log _ae$ | $(\ln x)’=\frac{1}{x}$ |
例题,$f(x)=x^x$,求该函数的导数(可应用求导的链式法则和乘法法则):
$\begin{equation}\begin{split}
f’(x) & =(x^x)’ \
& = (e^{x\ln x})’
& = e^{x\ln x}\cdot (x\ln x)’
& = x^x(\ln x+1)
\end{split}\end{equation}$
2.偏导数
偏导数存在于多元函数中,即自变量的数量多于一个。
以二元函数为例,如果$f(x,y)$是一个二元函数,而且存在$L_x$和$L_y$,使得:
\[f(x_0+\Delta x,y_0+\Delta y)=f(x_0,y_0)+L_x\Delta x+L_y\Delta y+o(\mid \Delta x \mid+\mid \Delta y \mid)\]那么$f(x,y)$在$f(x_0,y_0)$点处可微。且$L_x$、$L_y$分别是$f$在$x,y$方向上的偏导数。即,
\[\frac{\partial}{\partial x}f(x_0,y_0)=L_x;\frac{\partial}{\partial y}f(x_0,y_0)=L_y\]👉高阶偏导数:(以二阶为例)
\[\frac{\partial ^2}{\partial x^2}f(x_0,y_0)=L_{x^2};\frac{\partial ^2}{\partial y^2}f(x_0,y_0)=L_{y^2};\frac{\partial ^2}{\partial x \partial y}f(x_0,y_0)=L_{xy}\]【例题1】求$f(x,y)=ln(x+y^2)$的一阶偏导数:
\[\frac{\partial}{\partial x}f(x,y)=\frac{1}{x+y^2};\frac{\partial}{\partial y}f(x,y)=\frac{2y}{x+y^2}\]【例题2】求$z=e^{x+2y}$的所有二阶偏导数:
先求一阶偏导数:
\[\frac{\partial z}{\partial x}=e^{x+2y};\frac{\partial z}{\partial y}=2e^{x+2y}\]然后求二阶偏导数:
\[\frac{\partial ^2z}{\partial x^2}=e^{x+2y};\frac{\partial ^2z}{\partial y^2}=4e^{x+2y}\] \[\frac{\partial ^2z}{\partial x \partial y}=\frac{\partial}{\partial y}(\frac{\partial z}{\partial x})=\frac{\partial}{\partial y}(e^{x+2y})=2e^{x+2y} \tag 1\] \[\frac{\partial ^2z}{\partial y \partial x}=\frac{\partial}{\partial x}(\frac{\partial z}{\partial y})=\frac{\partial}{\partial x}(2e^{x+2y})=2e^{x+2y} \tag 2\]其中,式(1)是先x后y,式(2)是先y后x,二者得到的结果是相等的。但是并不意味着所有这种情况都是相等的,相等的条件为:若二元函数$z=f(x,y)$在点$(x,y)$存在直到$n$阶的连续混合偏导数,则在这一点$m(m\leqslant n)$阶混合偏导数都与顺序无关(可推广至多元函数)。
符号的差异:如果式中只有一个自变量,则求导式中使用$d$;如果式中有两个及以上的自变量,则使用偏导符号$\partial$。两个符号含义相同,只是应用场景不同而已。
3.方向导数
在函数定义域内的点,对某一个方向求导得到的导数。一般为二元函数和三元函数的方向导数,方向导数可分为沿直线方向和沿曲线方向的方向导数。
方向导数的定义:设函数$z=f(x,y)$在点$P(x,y)$的某一邻域$U(P)$内有定义,自$P$点引射线$l$,自$x$轴的正向到射线$l$的转角为$\varphi$,$P’(x+\Delta x,y+\Delta y)\in U(P)$为$l$上的另一点,若
\[\lim_{\rho \to 0}\frac{f(x+\Delta x,y+\Delta y)-f(x,y)}{\rho},(\rho =\sqrt{(\Delta x^2)+(\Delta y^2)})\]存在,则称此极限值为$f(x,y)$在点$P$沿方向$l$的方向导数,记作$\frac{\partial f}{\partial l}$,其计算公式为:
\[\frac{\partial f}{\partial l}=\frac{\partial f}{\partial x}\cos \varphi+\frac{\partial f}{\partial y}\sin \varphi\]方向导数的定义类似于导数,分母是$\sqrt{(\Delta x^2)+(\Delta y^2)}$,分子其实就是$\Delta z$,其比值就是三角函数中$\tan$的值。
👉一个点在所有方向均可能存在方向导数。
3.1.方向导数与偏导数
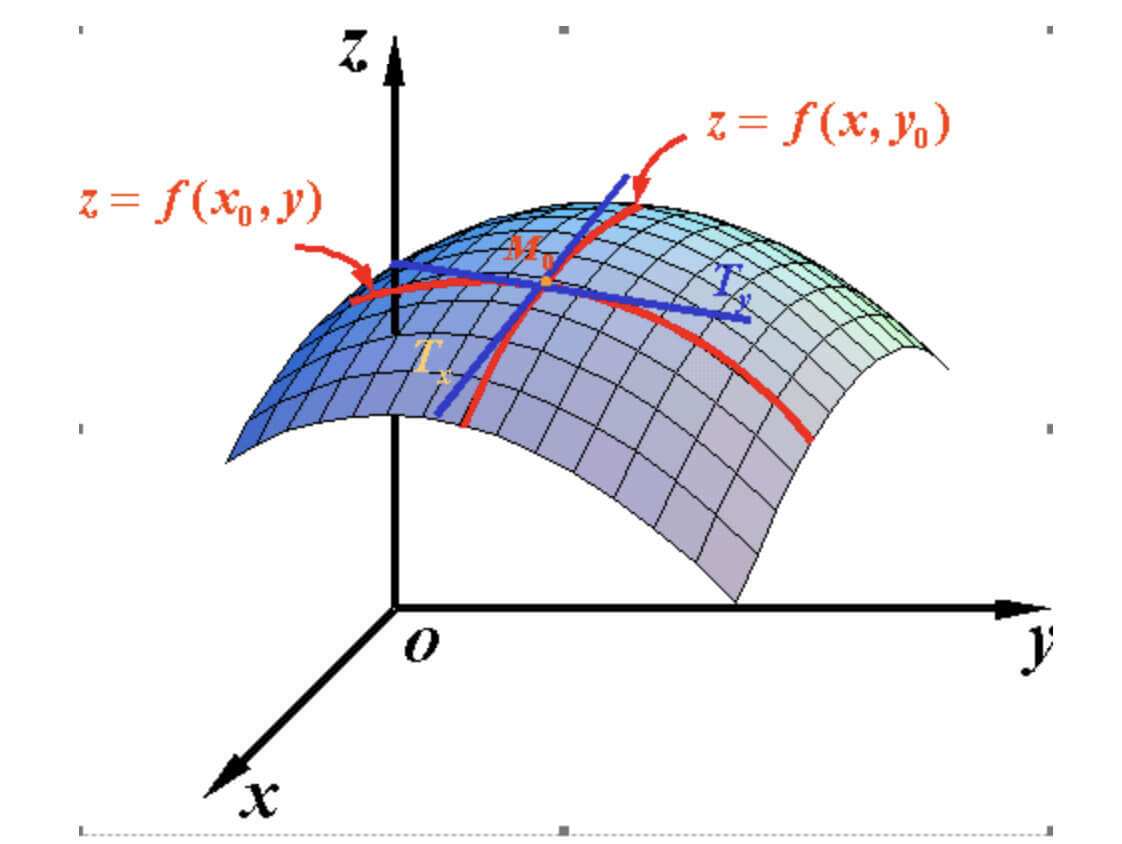
偏导数$f_x(x,y)$指的是函数在$y$方向不变,函数值沿着$x$轴方向的变化率。其实就是$\varphi=0^\circ$时的方向导数。
偏导数$f_y(x,y)$指的是函数在$x$方向不变,函数值沿着$y$轴方向的变化率。其实就是$\varphi=90^\circ$时的方向导数。
3.2.方向导数公式的推导
3.2.1.代数法
$f(x+\Delta x,y+\Delta y)-f(x,y)=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+o(\rho)$
$x$增量为$\Delta x$时,如果$y$不变的话,$z$的增量为$\frac{\partial f}{\partial x}\Delta x$
$\frac{f(x+\Delta x,y+\Delta y)-f(x,y)}{\rho} = \frac{\partial f}{\partial x}\cdot \frac{\Delta x}{\rho}+ \frac{\partial f}{\partial y}\cdot \frac{\Delta y}{\rho} + \frac{o(\rho)}{\rho} = \frac{\partial f}{\partial x}\cos \varphi+\frac{\partial f}{\partial y}\sin \varphi$
3.2.2.几何法
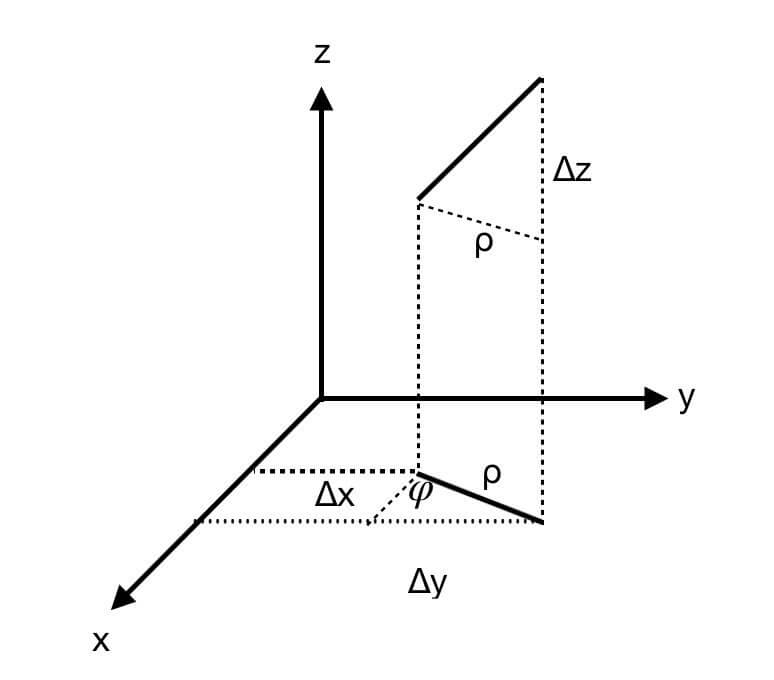
$\Delta z=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y$
$\rho=\sqrt{(\Delta x)^2+(\Delta y)^2}$
又$\cos \varphi=\frac{\Delta x}{\rho}$;$\sin \varphi=\frac{\Delta y}{\rho}$
所以,$\frac{\partial f}{\partial l}=\frac{\Delta z}{\rho}=\frac{\partial f}{\partial x}\cdot \frac{\Delta x}{\rho}+ \frac{\partial f}{\partial y}\cdot \frac{\Delta y}{\rho}=\frac{\partial f}{\partial x}\cos \varphi+\frac{\partial f}{\partial y}\sin \varphi$