【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.偏差-方差分解
对学习算法除了通过实验估计其泛化能力,人们往往还希望了解它“为什么”具有这样的性能。“偏差-方差分解”(bias-variance decomposition)是解释学习算法泛化性能的一种重要工具。
偏差-方差分解试图对学习算法的期望泛化错误率进行拆解。
| 符号 | 解释 |
|---|---|
| $x$ | 测试样本 |
| $D$ | 训练集 |
| $y_D$ | $x$在数据集中的标记 |
| $y$ | $x$的真实标记 |
| $f$ | 训练集$D$学得的模型 |
| $f(x;D)$ | 由训练集$D$学得的模型$f$对$x$的预测输出 |
| $\overline{f}(x)$ | 模型$f$对$x$的期望预测输出 |
⚠️有可能出现噪声使得$y_D\neq y$。
👉以回归任务为例:
学习算法的期望预测为($\mathbb{E}$为期望符号):
\[\overline{f}(x)=\mathbb{E}_D[f(x;D)]\]即$\overline{f}(x)=\frac{1}{n}(f(x;D_1)+f(x;D_2)+…+f(x;D_n))$,其中,$D_1,D_2,…,D_n$为样本数相同的不同训练集。因为算法在不同训练集上学得的结果很可能不同,即便这些训练集是来自同一个分布。
使用样本数相同的不同训练集产生的方差为:
\[var(x)=\mathbb{E}_D[(f(x;D)-\overline{f}(x))^2]\]即$var(x)=\frac{1}{n}((f(x;D_1)-\overline{f}(x))^2+(f(x;D_2)-\overline{f}(x))^2+…+(f(x;D_n)-\overline{f}(x))^2)$
噪声为:
\[\varepsilon^2=\mathbb{E}_D[(y_D-y)^2]\]测试样本$x$可能有多个标记,即在不同的数据集中有不同的标记:$y_{D1},y_{D2},…,y_{Dn}$
期望输出与真实标记的差别称为偏差,即:
\[bias^2(x)=(\overline{f}(x)-y)^2\]偏差与$D$无关,因此去掉了$\mathbb{E}_D$。
为便于讨论,假定噪声期望为零,即$\mathbb{E}_D[y_D-y]=0$。
对算法的期望泛化误差进行分解:
\[\begin{align} E(f;D) & = \mathbb{E}_D[(f(x;D)-y_D)^2] \\ & = \mathbb{E}_D[(f(x;D)-\overline{f}(x)+\overline{f}(x)-y_D)^2] \\ & = \mathbb{E}_D[(f(x;D)-\overline{f}(x))^2] + \mathbb{E}_D[(\overline{f}(x)-y_D)^2]+\mathbb{E}_D[2(f(x;D)-\overline{f}(x))(\overline{f}(x)-y_D)] \\ & = \mathbb{E}_D[(f(x;D)-\overline{f}(x))^2]+\mathbb{E}_D[(\overline{f}(x)-y_D)^2] \\ & = \mathbb{E}_D[(f(x;D)-\overline{f}(x))^2] +\mathbb{E}_D[(\overline{f}(x)-y+y-y_D)^2] \\ & = \mathbb{E}_D[(f(x;D)-\overline{f}(x))^2]+\mathbb{E}_D[(\overline{f}(x)-y)^2]+\mathbb{E}_D[(y-y_D)^2]+2\mathbb{E}_D[(\overline{f}(x)-y)(y-y_D)] \\ & = \mathbb{E}_D[(f(x;D)-\overline{f}(x))^2] +(\overline{f}(x)-y)^2+\mathbb{E}_D[(y_D-y)^2] \\ & = var(x)+bias^2(x)+\varepsilon^2 \end{align}\]这里主要解释下第三步到第四步的推导。将第三步的最后一项展开:
\[\mathbb{E}_D [ 2(f(x;D)-\bar{f}(x)) (\bar{f}(x)-y_D)]=\mathbb{E}_D[2(f(x;D)-\bar{f}(x)) \cdot \bar{f}(x)] - \mathbb{E}_D[2(f(x;D)-\bar{f}(x))\cdot y_D] \tag{1.1}\]👉化简式(1.1)的第一项:
\[\mathbb{E}_D[2(f(x;D)-\bar{f}(x)) \cdot \bar{f}(x)] = \mathbb{E}_D[2f(x;D)\cdot \bar{f}(x)-2\bar{f}(x)\cdot \bar{f}(x)]\]由于$\bar{f}(x)$是常量,所以由期望的运算性质:$\mathbb{E}[AX+B]=A\mathbb{E}[X]+B$(其中A,B均为常量)可得:
\[\mathbb{E}_D[2(f(x;D)-\bar{f}(x)) \cdot \bar{f}(x)]=2\bar{f}(x) \cdot \mathbb{E}_D[f(x;D)]-2\bar{f}(x)\cdot \bar{f}(x)\]又$\overline{f}(x)=\mathbb{E}_D[f(x;D)]$,所以可得式(1.1)的第一项为0。
👉化简式(1.1)的第二项:
\[\mathbb{E}_D[2(f(x;D)-\bar{f}(x))\cdot y_D] =2\mathbb{E}_D [f(x;D)\cdot y_D] - 2\bar{f}(x) \cdot \mathbb{E}_D[y_D]\]由于噪声和f无关,所以$f(x;D)$和$y_D$是两个相互独立的随机变量,所以根据期望的运算性质:$\mathbb{E}[XY]=\mathbb{E}[X]\mathbb{E}[Y]$(其中X和Y为相互独立的随机变量)可得:
\[\begin{align} \mathbb{E}_D[2(f(x;D)-\bar{f}(x))\cdot y_D] &=2\mathbb{E}_D [f(x;D)\cdot y_D] - 2\bar{f}(x) \cdot \mathbb{E}_D[y_D] \\&= 2\mathbb{E}_D[f(x;D)]\cdot \mathbb{E}_D[y_D] - 2\bar{f}(x) \cdot \mathbb{E}_D[y_D] \\&= 2\bar{f}(x)\cdot \mathbb{E}_D[y_D] - 2\bar{f}(x) \cdot \mathbb{E}_D[y_D] \\&= 0\end{align}\]所以,式(1.1)的第二项也为0。
❗️也就是说,泛化误差可分解为偏差、方差与噪声之和。
⚠️偏差-方差分解,这样优美的形式仅在基于均方误差的回归任务中得以推导出。对于分类任务,由于0/1损失函数的跳变性,理论上推导出偏差-方差分解很困难。
2.偏差、方差、噪声
👉偏差:
度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。
👉方差:
度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。
👉噪声:
表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度。
因此,偏差-方差分解说明泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。
3.偏差-方差窘境
一般来说,偏差与方差是有冲突的,这称为偏差-方差窘境。
泛化误差与偏差、方差的关系示意图:
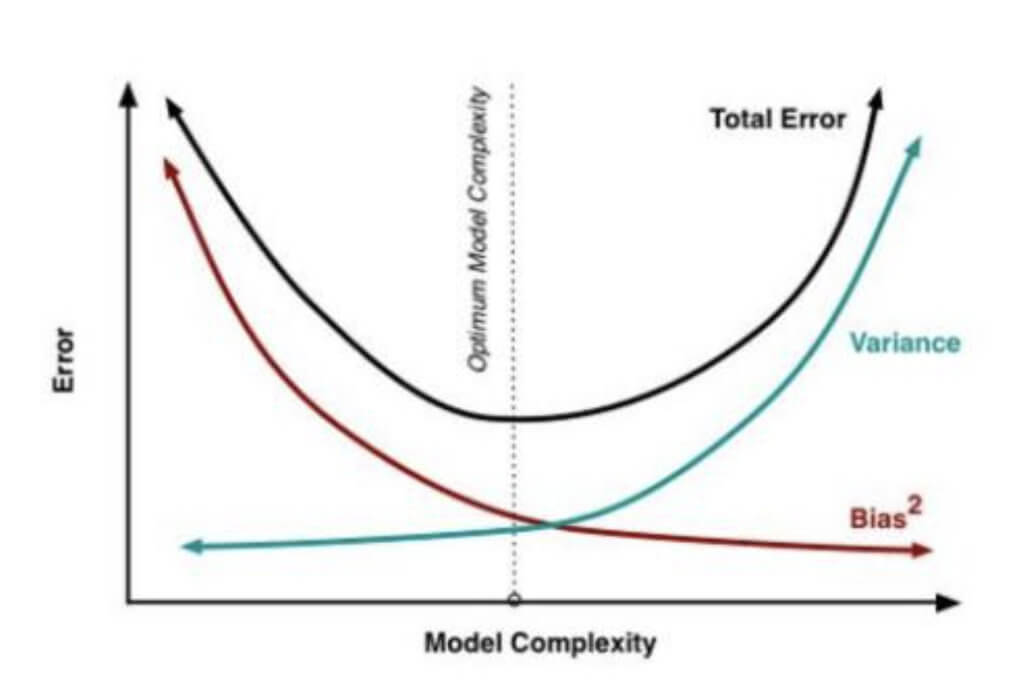
上图中,Total Error曲线的最低点,即Total Error最小时,此时,泛化误差最小。
给定学习任务,假定我们能控制学习算法的训练程度,则在训练不足时,学习器的拟合能力不够强,训练数据的扰动不足以使学习器产生显著变化,此时偏差主导了泛化错误率。
随着训练程度的加深,学习器的拟合能力逐渐增强,训练数据产生的扰动渐渐能被学习器学到,方差逐渐主导了泛化错误率。
在训练程度充足后,学习器的拟合能力已非常强,训练数据产生的轻微扰动都会导致学习器发生显著变化,若训练数据自身的、非全局的特性被学习器学到了,则将发生过拟合。
👉很多学习算法都可控制训练程度,例如决策树可控制层数,神经网络可控制训练轮数,集成学习方法可控制基学习器个数。
4.代价的类型
机器学习过程涉及很多类型的代价,除了常用的误分类代价,还有测试代价、标记代价、属性代价等。即便仅考虑误分类代价,仍可进一步划分为基于类别的误分类代价以及基于样本的误分类代价。
5.参考资料
- 泛化误差与偏差、方差的关系示意图来源:知乎:为什么xgboost/gbdt在调参时为什么树的深度很少就能达到很高的精度?—用户“于菲”的回答
- 南瓜书PumpkinBook