本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.微分定义
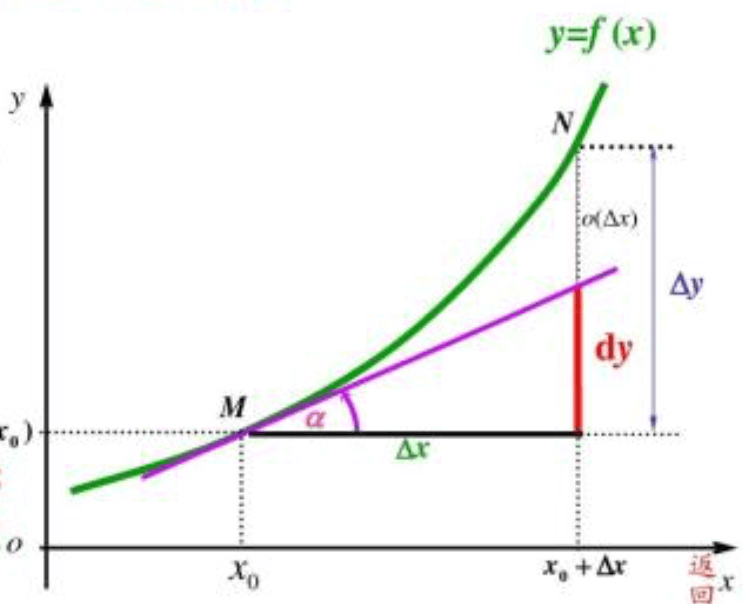
微分定义:若函数$y=f(x)$在点$x_0$处的增量可表示为:
\[\Delta y=f(x+\Delta x)-f(x)=A\Delta x+o(\Delta x)\]其中,$A$为不依赖于$\Delta x$的常数。则称函数$y=f(x)$在点$x_0$处🤜可微🤛,而$A\Delta x$称为点$x_0$的微分,记作$dy$或$df$,即:
\[dy=A\Delta x\]1.1.微分与导数
在上述微分定义中,有:
\[A=\frac{dy}{dx}\]即为导数。简单的说:
- 微分$dy$是增量(⚠️注意不是$\Delta y$,$\Delta y=dy+o(\Delta x)$)
- 导数$\frac{dy}{dx}$是斜率
1.2.可微条件
以二元函数为例:
❗️必要条件:
- 若函数在某点可微分,则函数在该点必连续。
- 若二元函数在某点可微分,则该函数在该点对x和y的偏导数必存在。
❗️充分条件:
- 若函数对x和y的偏导数在这点的某一邻域内都存在,且均在这点连续,则该函数在这点可微。
2.全微分
以二元函数为例:
如果函数$z=f(x,y)$在点$(x,y)$的全增量$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$可表示为$\Delta z=A\Delta x+B\Delta y+o(\rho),(\rho \to0)$,其中$A,B$仅与$x,y$有关,而不依赖于$\Delta x,\Delta y$,$\rho=\sqrt{(\Delta x)^2+(\Delta y)^2}$,则称函数$z=f(x,y)$在点$(x,y)$处可微分,$A\Delta x +B\Delta y$称为函数$z=f(x,y)$在点$(x,y)$处的全微分(⚠️全微分和偏微分都是针对一个点来说的),记作$dz$,即$dz=A\Delta x +B\Delta y$。
2.1.全微分与偏导数
若函数$z=f(x,y)$在点$(x,y)$处可微分,则该函数在点$(x,y)$的偏导数$\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}$必存在,且函数$z=f(x,y)$在点$(x,y)$的全微分为:
\[dz=\frac{\partial z}{\partial x} \Delta x+\frac{\partial z}{\partial y} \Delta y\]3.偏微分
在上述全微分定义中,$A\Delta x$和$B\Delta y$即为偏微分。简单说,即:
- y不变,只有x改变而导致的z的增量
- x不变,只有y改变而导致的z的增量
4.微分方程
🚩微分方程:指含有未知函数及其导数的关系式。
👉微分方程的阶:微分方程中所出现的未知函数的最高阶导数的阶数。
- 常微分方程:未知函数是一元函数(即只有一个自变量)的微分方程。
- 偏微分方程:未知函数是多元函数(即有两个或两个以上的自变量)的微分方程。