【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.线性判别分析
1.1.背景
线性判别分析(Linear Discriminant Analysis,简称LDA)是一种经典的线性学习方法。亦称“Fisher判别分析”,但是严格来说LDA与Fisher判别分析稍有不同,前者假设了各类样本的协方差矩阵相同且满秩。
👉LDA的思想:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。二维示意图见下:
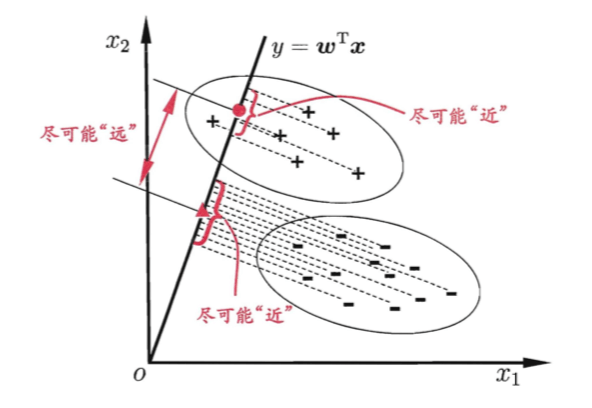
图中,+、-分别代表正例和反例,椭圆表示数据簇的外轮廓,虚线表示投影,红色实心圆和实心三角形分别表示两类样本投影后的中心点。
我们所要做的就是确定这样一个投影向量$\mathbf w$,经过$\mathbf w^T\mathbf x$的投影变换后,类间距离最大,类内方差最小。
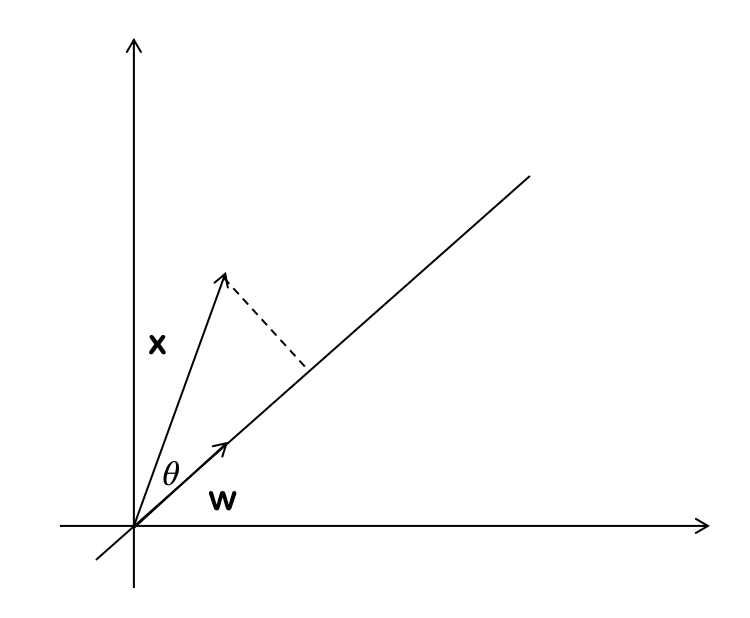
将样本$\mathbf x$投影到直线,其中$\mathbf w$决定了直线的方向。$y=\mathbf w^T \mathbf x$中,假设$\mathbf w$的模为1,则y为$\mathbf x$投影到$\mathbf w$(即方向为$\mathbf w$的直线)的长度,因为$\mathbf w^T \mathbf x=\parallel \mathbf w \parallel \parallel \mathbf x \parallel \cos \theta=\parallel \mathbf x \parallel \cos \theta$,如下图所示:
1.2.推导过程
给定数据集$D=\{(\mathbf x_i,y_i)\}_{i=1}^m$,$y_i\in\{0,1 \}$。(这里i指的是数据集中的第i个样本)。
然后令$X_i,\mu_i,\Sigma_i$分别表示第i类的示例集合、均值向量、协方差矩阵。(这里的i指的是类别,假设是二分类,有$i\in \{0,1 \}$)。
1.2.1.类间距离
假设$X_0$为:
\[\begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{d1} & x_{d2} & \cdots & x_{dm} \\ \end{pmatrix}\]其中m为数据条数,即样本量。每一列为一个样本,d为特征数,即维数。$X_0$中的数据对应的标签均为$y_0$。
对$X_0$中的每一行求均值,即求每个特征的均值,可得到$\mu_0$:
\[\begin{pmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_d \\ \end{pmatrix}\]投影向量$\mathbf w$为:
\[\begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_d \\ \end{pmatrix}\]类标为0的点的均值向量投影到直线上得到的实数为:$\mathbf w^T \mu_0$,即类标为0的数据簇的中心点在直线上投影点的y值,可以理解为$\bar y_0$;同理,类标为1的点的均值向量投影到直线上得到的实数为:$\mathbf w^T \mu_1$,同样的,可以理解为$\bar y_1$。
👉此时可以得到类间距离(即$(\bar y_0-\bar y_1)^2$):
\[\begin{align} (\mathbf w^T\mu_0-\mathbf w^T\mu_1)^2 & = (\mathbf w^T(\mu_0-\mu_1))^2 \\ & = (\mathbf w^T(\mu_0-\mu_1))((\mu_0-\mu_1)^T\mathbf w) \\ & = \mathbf w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\mathbf w \\ \end{align}\]1.2.2.类内方差
“投影以后组内的方差之和尽量小”(这里的方差没有除以样本量)用数学表达出来就是:
类标为0的点投影到直线上的方差是:
\[\sum_{x\in X_0}(\mathbf w^Tx-\mathbf w^T\mu_0)^2\]类标为1的点投影到直线上的方差是:
\[\sum_{x\in X_1}(\mathbf w^Tx-\mathbf w^T\mu_1)^2\]它们的和是:
\[\begin{align} \sum_{x\in X_0}(\mathbf w^Tx-\mathbf w^T\mu_0)^2 + \sum_{x\in X_1}(\mathbf w^Tx-\mathbf w^T\mu_1)^2 & =\sum_{x\in X_0}\mathbf w^T(x-\mu_0)(x-\mu_0)^T\mathbf w+\sum_{x\in X_1}\mathbf w^T(x-\mu_1)(x-\mu_1)^T\mathbf w \\ & = \mathbf w^T \sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^T \mathbf w + \mathbf w^T \sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^T \mathbf w \end{align}\]令:
\[\Sigma_0=\sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^T\] \[\Sigma_1=\sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^T\]👉因此,类内方差之和可表示为:
\[\mathbf w^T \Sigma_0 \mathbf w+\mathbf w^T \Sigma_1 \mathbf w\]1.2.3.广义瑞利商
欲使同类样例的投影点尽可能接近,可以让同类样例投影点的协方差尽可能小,即$\mathbf w^T \Sigma_0 \mathbf w+\mathbf w^T \Sigma_1 \mathbf w$尽可能小。
而欲使异类样例的投影点尽可能远离,可以让类中心之间的距离尽可能大,即$\parallel \mathbf w^T\mu_0-\mathbf w^T\mu_1 \parallel ^2_2$尽可能大。
同时考虑二者,则可得到欲最大化的目标:
\[\begin{align} J & =\frac{\parallel \mathbf w^T\mu_0-\mathbf w^T\mu_1 \parallel ^2_2}{\mathbf w^T \Sigma_0 \mathbf w+\mathbf w^T \Sigma_1 \mathbf w} \\ & = \frac{\mathbf w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\mathbf w}{\mathbf w^T (\Sigma_0+\Sigma_1)\mathbf w} \end{align} \tag{1.1}\]👉定义“类内散度矩阵”(within-class scatter matrix):
\[\begin{align} S_w & =\Sigma_0+\Sigma_1 \\ & = \sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^T + \sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^T \end{align}\]👉以及“类间散度矩阵”(between-class scatter matrix):
\[S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T\]则式(1.1)可重新写为:
\[J=\frac{\mathbf w^T S_b \mathbf w}{\mathbf w^T S_w \mathbf w} \tag{1.2}\]👉这就是LDA欲最大化的目标,即$S_b$和$S_w$的“广义瑞利商”(generalized Rayleigh quotient)。
1.2.4.参数估计
那么,现在只剩下一个最终目的,即确定$\mathbf w$使得式(1.2)得到最大值,其他均为已知量。
观察式(1.2)可以发现,若$\mathbf w’$是最大化式(1.2)的解的话,那么对于任意常数$\alpha$,$\alpha \mathbf w’$也是式(1.2)最大化时的解。因为$\alpha$改变的是向量$\mathbf w’$的长度,因此,可以说式(1.2)的解与$\mathbf w$的长度无关,只与其方向有关。
不失一般性,令$\mathbf w^T S_w \mathbf w=1$,则式(1.2)等价于:
\[\begin{align*} &\min \limits_{w} \quad -\mathbf w^T S_b \mathbf w \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& \mathbf w^TS_w \mathbf w =1 \\ \end{array} \end{align*} \tag{1.3}\]令$\mathbf w^TS_w \mathbf w$等于一个确定的值,我们可以求出一个确定的$\mathbf w$值。与等于其他确定值情况下求出来的$\mathbf w’$呈正比关系,即$\mathbf w=\alpha \mathbf w’$。
$s.t.$符号:subject to,受限制于….,即约束条件。
例如:目标函数为$min(x+2)$,约束条件为$s.t. \quad x=\{1,2,3\}$,即x的取值为1,2,3时,求x+2的最小值。
由拉格朗日乘子法(详见第2.1部分),式(1.3)等价于$S_b\mathbf w=\lambda S_w \mathbf w$。
因为:
\[S_b\mathbf w=(\mu_0-\mu_1)(\mu_0-\mu_1)^T \mathbf w\]其中$(\mu_0-\mu_1)^T\mathbf w$为标量,假设$\lambda_{\mathbf w}=(\mu_0-\mu_1)^T\mathbf w$,则有:
\[\lambda_{\mathbf w}(\mu_0-\mu_1)=\lambda S_w\mathbf w \Longrightarrow S_w^{-1}(\mu_0-\mu_1)=\frac{\lambda}{\lambda_{\mathbf w}}\mathbf w\]其中可以让$\alpha=\frac{\lambda}{\lambda_{\mathbf w}}$,根据前文所提过的,$\frac{\lambda}{\lambda_{\mathbf w}}\mathbf w$和$\mathbf w$都是式1.2(或式1.3)的解。因此上式可以简化为:
\[\mathbf w=S_w^{-1}(\mu_0-\mu_1)\]1.3.将LDA推广到多分类
假定存在N个类,且第i类示例数为$m_i$。
先定义“全局散度矩阵”:
\[\begin{align} S_t&=S_b+S_w \\& =\sum^m_{i=1}(\mathbf x_i-\mu)(\mathbf x_i-\mu)^T \end{align}\]其中$\mu$是所有示例的均值向量。将类内散度矩阵重定义为每个类别的散度矩阵之和,即
\[S_w=\sum^N_{i=1}S_{w_i}\]其中
\[S_{w_i}=\sum \limits_{\mathbf x\in X_i}(\mathbf x-\mu_i)(\mathbf x-\mu_i)^T\]因此可计算得到:
\[\begin{align} S_b&=S_t-S_w \\& = \sum ^N_{i=1}m_i(\mu_i-\mu)(\mu_i-\mu)^T \end{align}\]例如:三分类问题如下图所示
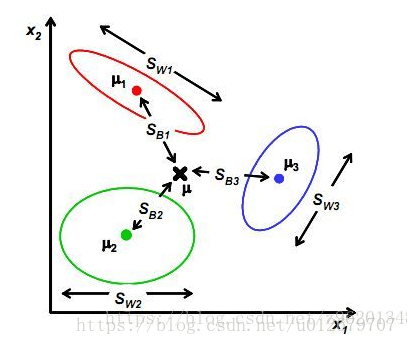
显然,多分类LDA可以有多种实现方法:使用$S_b,S_w,S_t$三者中的任何两个即可。常见的一种实现是采用优化目标:
\[\max \limits_{\mathbf w} \frac{tr(\mathbf w^TS_b \mathbf w)}{tr(\mathbf w^TS_w\mathbf w)}\]其中$\mathbf w\in \mathbb R^{d\times (N-1)}$,$tr(\cdot)$表示矩阵的迹。
2.约束下的最优化算法
在约束下,求解最优化问题最常见的两种方法:
- 【有等式约束时】:拉格朗日乘子法。
- 【有不等式约束时】:KKT条件。
即求其在指定作用域上的全局最小值。
如果没有约束条件,对于凸函数来说可使其一阶导等于0,或可用梯度下降法或牛顿法。
2.1.拉格朗日乘子法
拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子,可将有d个变量与k个约束条件的最优化问题转化为具有d+k个变量的无约束优化问题求解。
举个二维优化的例子:
\[\begin{align*} &\min \quad f(x,y) \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& g(x,y)=0 \\ \end{array} \end{align*}\]这里画出$f(x,y)$的等高线图:
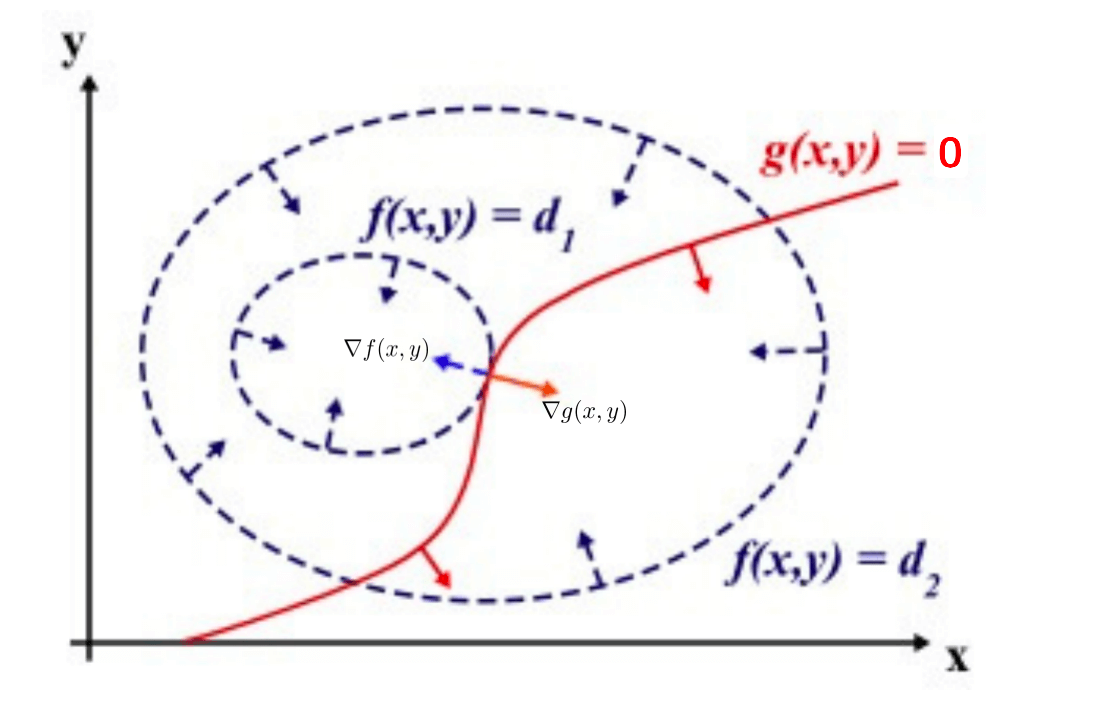
图中$d_1<d_2$,箭头均指向梯度下降的方向。
加上约束之后,$f(x,y)$的最小点显然应该在$f(x,y)$的等高线正好和约束线相切的位置。因为如果只是相交意味着肯定还存在其他的等高线在该条等高线的内部或者外部,使得新的等高线与$g(x,y)$的交点的值更大或者更小,只有等高线与$g(x,y)$相切的时候,才可能取到最优值(即最大值或者最小值)。
所以在最优点,有梯度$\nabla g(x,y)$和$\nabla f(x,y)$的方向必相同或者相反,即存在$\lambda \neq 0$,使得:
\[\nabla f(x,y)+\lambda \nabla g(x,y)=0 \tag{2.1}\]$\lambda$称为拉格朗日乘子,定义拉格朗日函数:
\[L(x,y,\lambda)=f(x,y)+\lambda g(x,y) \tag{2.2}\]根据式(2.1),有$\nabla L(x,y,\lambda)=0$。
👉举个应用例子:
\[\begin{align*} &\max \quad f(x,y,z)=8xyz \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 \\ \end{array} \end{align*}\]其中,约束条件可定义为:
\[g(x,y,z)=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1=0\]先定义拉格朗日函数:
\[\begin{align} L(x,y,z,\lambda)&=f(x,y,z)+\lambda g(x,y,z) \\ &= 8xyz+\lambda(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1) \end{align}\]因为在最大点(极值点)有$\nabla L(x,y,z,\lambda)=0$,所以:
\[\frac{\partial L(x,y,z,\lambda)}{\partial x} = 8yz+\frac{2\lambda x}{a^2}=0 \tag{2.3}\] \[\frac{\partial L(x,y,z,\lambda)}{\partial y} = 8xz+\frac{2\lambda y}{b^2}=0 \tag{2.4}\] \[\frac{\partial L(x,y,z,\lambda)}{\partial z} = 8xy+\frac{2\lambda z}{c^2}=0 \tag{2.5}\] \[\frac{\partial L(x,y,z,\lambda)}{\partial \lambda}=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1=0 \tag{2.6}\]联立式(2.3)、式(2.4)、式(2.5)、式(2.6),可得:
\[x=\frac{\sqrt 3 a}{3};y=\frac{\sqrt 3 b}{3};z=\frac{\sqrt 3 c}{3}\]最终可解得,在约束条件下:
\[\max \quad f(x,y,z)=\frac{8\sqrt 3}{9}abc\]👉回到式(1.3)
假设,$f(\mathbf w)=-\mathbf w^T S_b \mathbf w ; g(\mathbf w)=\mathbf w^T S_w \mathbf w$,可求得$\nabla f(\mathbf w)=-2S_b\mathbf w ; \nabla g(\mathbf w)=2S_w\mathbf w$。根据式(2.1),因此在极值点有:$-2S_b\mathbf w+2\lambda S_w\mathbf w=0$,即$S_b\mathbf w=\lambda S_w \mathbf w$。
2.2.KKT条件
KKT条件(Karush-Kuhn-Tucker,简称KKT)主要用于不等式约束下的优化问题。例如:
\[\begin{align*} &\min \limits_{x} \quad f(x) \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& g(x) \leqslant 0 \\ \end{array} \end{align*} \tag{2.7}\]只考虑在$\min f(x)$和$g(x) \leqslant 0$的情况即可。因为其他形式都可转化为此形式,比如$\max f(x)$取负数或负对数等操作,可改为求最小值。$g(x)\geqslant 0$可以变为$-g(x) \leqslant 0$,$g(x) \leqslant c$可以变为$g(x)-c\leqslant 0$等等。
式(2.7)对应的拉格朗日函数为:$L(x,\lambda)=f(x)+\lambda g(x)$。
- 当可行解落在$g(x) < 0$区域内时,此时直接最小化$f(x)$即可。
- 当可行解落在$g(x)=0$,即边界上,此时等价于等式约束优化问题。
以上两种情况,无论哪种情况都会得到:$\lambda g(x)=0$,因为:
- 如果可行解落在约束边界上即得$g(x)=0$($\lambda \neq 0$),从而有$\lambda g(x)=0$。
- 如果可行解落在约束区域内部,此时约束不起作用,令$\lambda=0$,消去约束即可。
在式(2.7)的情况下,若$\lambda \neq 0$,即可行解落在边界上,则应该有$-\nabla_xf(x)=\lambda \nabla_x g(x)$,并且$\lambda>0$,见下图右侧所示情况:
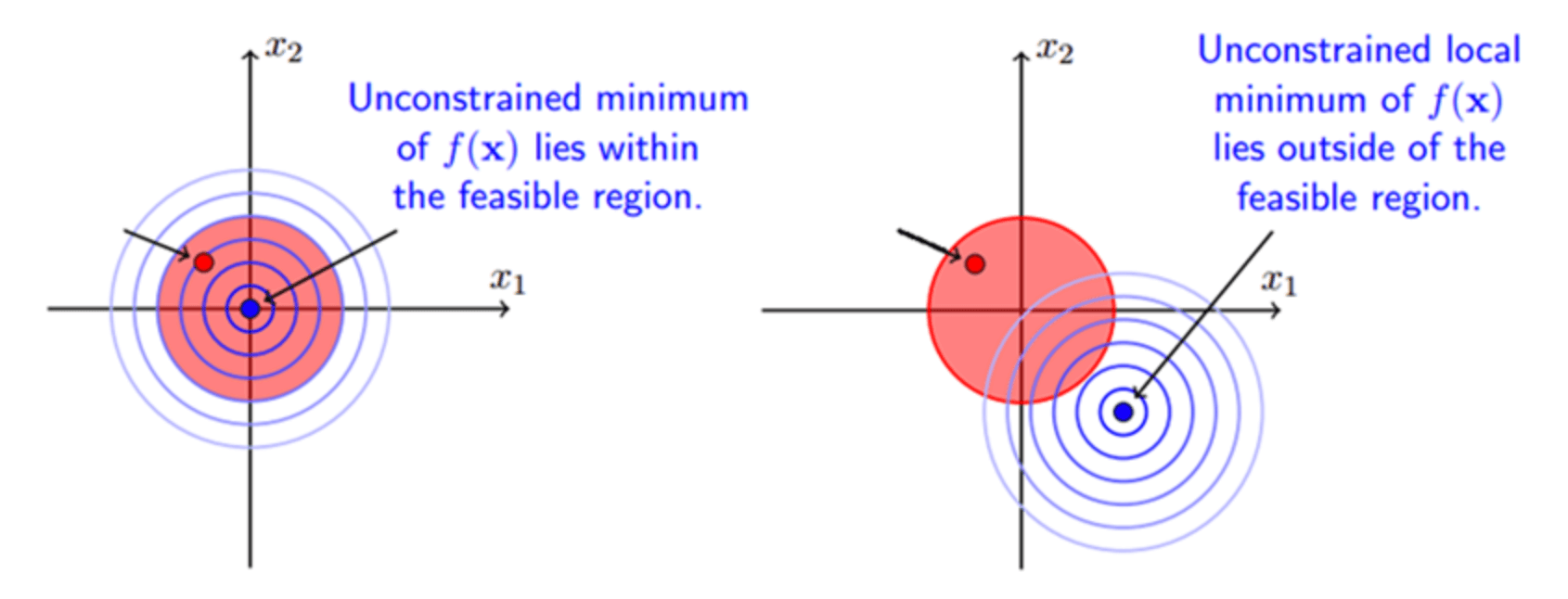
拉格朗日乘子法:$\nabla g(x)$和$\nabla f(x)$方向相同或者相反。(前提条件:$\min f(x)$,约束条件为$g(x)=0$)。
KKT条件:$\nabla g(x)$和$\nabla f(x)$方向相反。(前提条件为:$\min f(x)$,约束条件为$g(x) \leqslant 0$)。
然后通过以下方程组求最后的解:
\[\left \{ \begin{array}{c} g(x) \leqslant 0 \\ \lambda \geqslant 0 \\ \lambda g(x) =0 \\ \nabla_x L = \nabla f + \lambda \nabla g(x) =0 \end{array} \right.\]2.2.1.KKT条件的推广
KKT条件可以推广到多个约束,考虑具有m个等式约束和n个不等式约束,且可行域$\mathbb D \subset \mathbb R^d$非空的优化问题:
\[\begin{align*} &\min \limits_{x} \quad f(x) \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& h_i(x)=0 (i=1,...,m), \\& g_i(x) \leqslant 0 (j=1,...,n). \\ \end{array} \end{align*} \tag{2.8}\]引入拉格朗日乘子$\mathbf \lambda=(\lambda_1,\lambda_2,…,\lambda_m)^T$和$\mathbf \mu=(\mu_1,\mu_2,…,\mu_n)^T$,相应的拉格朗日函数为:
\[L(\mathbf x,\mathbf \lambda,\mathbf \mu)=f(\mathbf x)+\sum_{i=1}^m \lambda_ih_i(\mathbf x)+\sum_{j=1}^n\mu_jg_j(\mathbf x) \tag{2.9}\]由不等式约束引入的KKT条件($j=1,2,…,n$)为:
\[\begin{equation} \left\{ \begin{array}{l} g_j(\mathbf x) \leqslant 0;\\ \mu_j \geqslant 0;\\ \mu_jg_j(\mathbf x)=0.\\ \end{array} \right. \end{equation} \tag{2.10}\]一个优化问题可以从两个角度来考虑,即“主问题”和“对偶问题”。对于主问题式2.8,基于式2.9,其拉格朗日“对偶函数”$\Gamma$:$\mathbb R ^m \times \mathbb R^n \mapsto \mathbb R$定义为:
\[\begin{align} \Gamma(\mathbf \lambda,\mathbf \mu) & = \inf \limits_{\mathbf x \in \mathbb D} L(\mathbf x,\mathbf \lambda,\mathbf \mu) \\ & = \inf \limits_{\mathbf x \in \mathbb D} (f(\mathbf x)+\sum^m_{i=1}\lambda_ih_i(\mathbf x)+\sum^n_{j=1}\mu_j g_j(\mathbf x)) \end{align} \tag{2.11}\]在推导对偶问题时,常通过将拉格朗日乘子$L(\mathbf x,\mathbf \lambda ,\mathbf \mu)$对$\mathbf x$求导并令导数为0,来获得对偶函数的表达形式。
若$\tilde{x} \in \mathbb D$为主问题式2.8可行域中的点(即符合s.t.条件的点),则对任意$\mu \succeq 0$和$\mathbf \lambda$都有:
\[\sum^m_{i=1}\lambda_ih_i(\tilde{\mathbf x})+\sum^n_{j=1}\mu_j g_j(\tilde{\mathbf x})\leqslant 0\]$\mu \succeq 0$表示$\mathbf \mu$的分量均为非负。
进而有:
\[\Gamma(\mathbf \lambda,\mathbf \mu)=\inf \limits_{\mathbf x\in \mathbb D}L(\mathbf x,\lambda,\mu)\leqslant L(\tilde{\mathbf x},\lambda,\mu)\leqslant f(\tilde{\mathbf x})\]若主问题式2.8的最优值为$p^*$,则对任意$\mu \succeq 0$和$\mathbf \lambda$都有:
\[\Gamma(\lambda,\mu)\leqslant p^*\]即对偶函数给出了主问题最优值的下界。显然,这个下界取决于$\mu$和$\lambda$的值。于是,一个很自然的问题是:基于对偶函数能获得的最好下界是什么?这就引出了优化问题:
\[\max \limits_{\lambda,\mu} \Gamma(\lambda,\mu) \quad s.t.\mu \succeq 0 \tag{2.12}\]式2.12就是主问题式2.8的对偶问题,其中$\lambda$和$\mu$称为“对偶变量”。无论主问题式2.8的凸性如何,对偶问题式2.12始终是凸优化问题。
考虑式2.12的最优值$d^*$,显然有$d^* \leqslant p^*$,这称为“弱对偶性”成立;若$d^*=p^*$,则称为“强对偶性”。
3.上确界和下确界
👉上确界:
$\sup$:表示“上确界”。上界中的最小值。
上确界是一个集合的最小上界。
例子:
- $\sup \{1,2,3\}=3;$
- $\sup \{x\in R,0<x<1 \}=\sup \{x\in R,0\leqslant x \leqslant 1 \}=1$
- $\sup\{(-1)^n-1/n ; n=1,2,3,… \}=1$
- $\sup\{a+b;a\in A \ and \ b\in B \}=\sup(A)+\sup(B)$
👉下确界:
$\inf$:表示“下确界”。对于函数$y=f(x)$,在使$f(x)$大于等于N成立的所有常数M中,我们把M的最大值max(M)(即函数$y=f(x)$的最小值)叫做函数$y=f(x)$的下确界。
简单的说就是,在所有下界中如果有一个最大的下界,就称之为M的下确界。
例子:
- $\inf \{1,2,3 \}=1$
- $\inf \{x\in R,0<x<1 \}=0$
- $\inf \{(-1)^n+1/n;n=1,2,3,…\}=-1$
3.1.sup、inf和max、min的区别
sup和inf总是存在的,而函数的min和max有时候并不存在。
例如函数:$f(x)=\sin(x)/x$的图像:
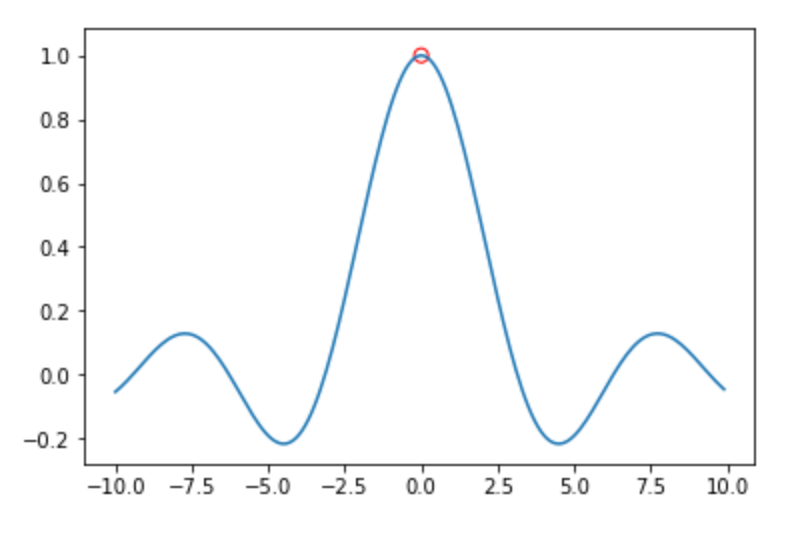
该函数在$x=0$处没有值,因此其最大值即max不存在,但是可以看出$f(x)$最小的上界为1,即$\sup f(x)=1$。