【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.神经网络表示
我们在【深度学习基础】第三课:什么是神经网络中已经初步接触了神经网络的表示方式。我们在这里再复习一下:
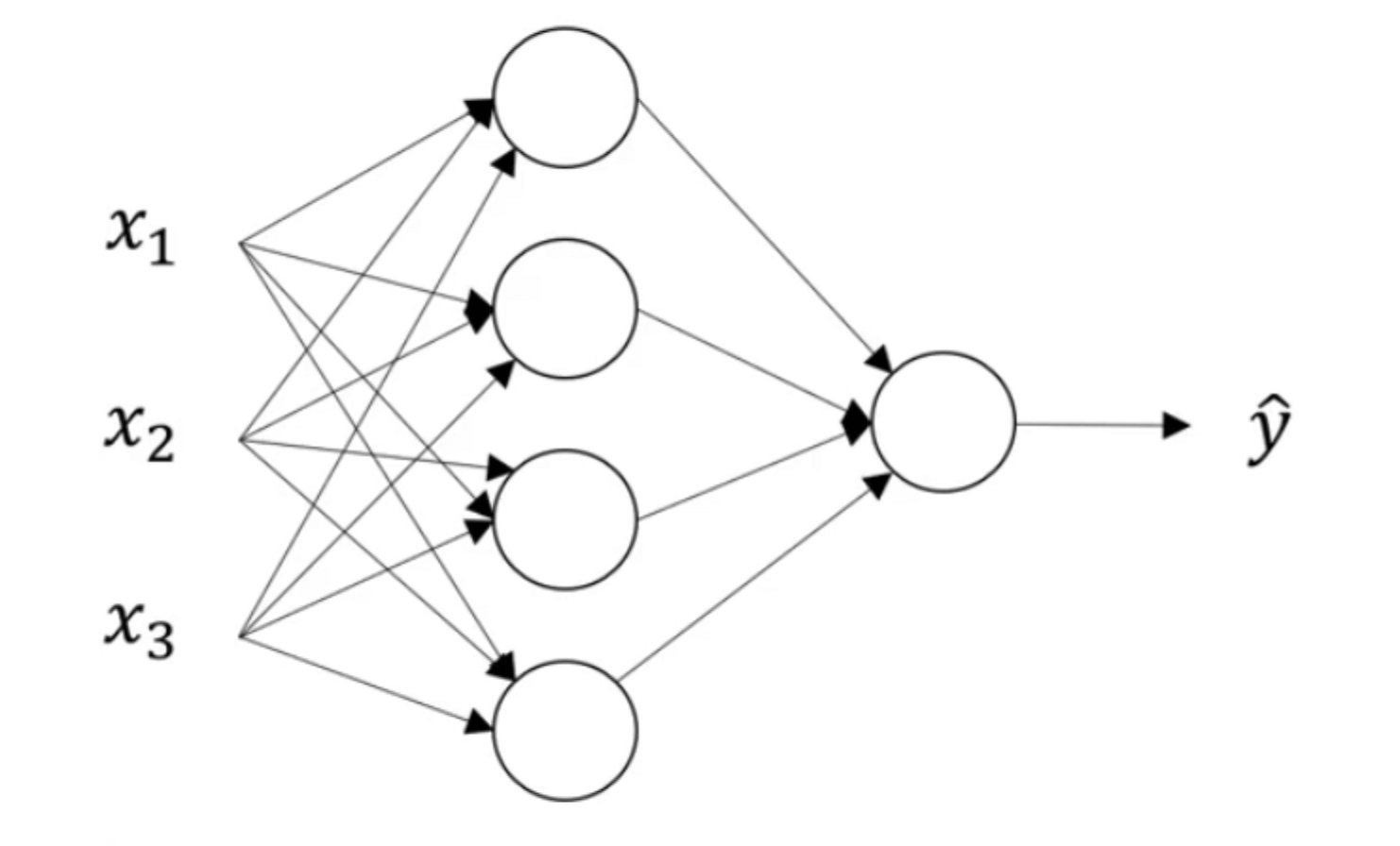
如上图所示,这是一个神经网络图。接下来我们对网络图中各个部分进行命名:
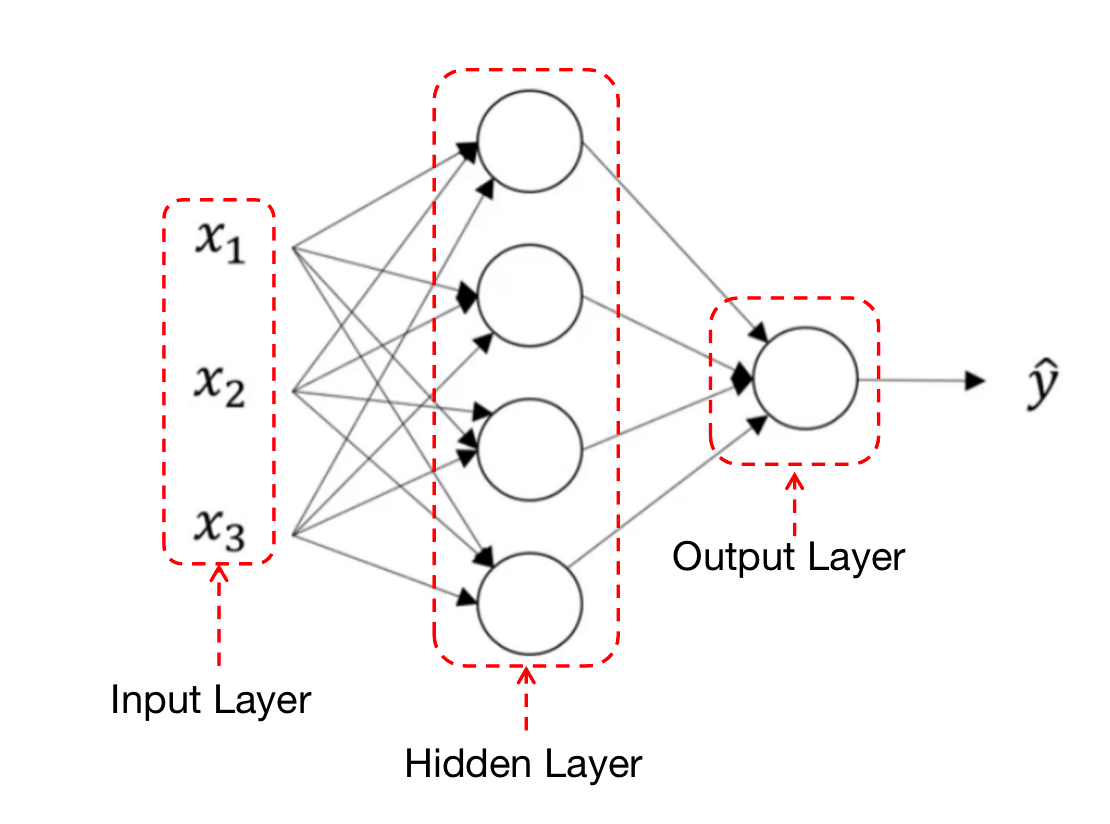
其中,“隐藏层”的含义是:在训练集中,我们不知道这些中间节点的真正数值。也就是说,你能看到输入层和输出层节点的数值,但是看不到隐藏节点的数值。
此外,之前在【深度学习基础】第四课:正向传播与反向传播中已经定义了一些符号,在此基础上我们继续定义一些新的符号以供后续使用:
- 输入层的值可表示为$a^{[0]}=X$。右上角的
[0]表示所处的层数,此处为第0层,即输入层。 - 可用$a^{[1]}$表示隐藏层的值,其中四个隐藏神经元的值分别为:$a^{[1]}_1$、$a^{[1]}_2$、$a^{[1]}_3$和$a^{[1]}_4$(右下角的数字表示是第几个神经元)。因此,$a^{[1]}$为$4\times 1$维的列向量:
- 以此类推,可用$a^{[2]}$表示输出层的值。本例中$a^{[2]}$为一个实数,即$a^{[2]}=\hat{y}$。
通过对这些符号的约定,我们可以很容易的知道该值来自于哪一层哪个神经元。
⚠️这里举例所用的神经网络是一个双层神经网络:第一层为隐藏层,第二层为输出层。输入层为第零层,通常不算在内。
❗️隐藏层和输出层都是有参数的。可以用$w^{[1]},b^{[1]}$和$w^{[2]},b^{[2]}$表示对应层的参数,并且$w^{[1]}$的维数为$4\times 3$,$b^{[1]}$的维数为$4\times 1$,$w^{[2]}$的维数为$1\times 4$,$b^{[2]}$的维数为$1\times 1$(关于维数后续部分会有详细的讲解)。
2.计算神经网络的输出
假设激活函数为sigmoid函数,针对单个神经元来说:
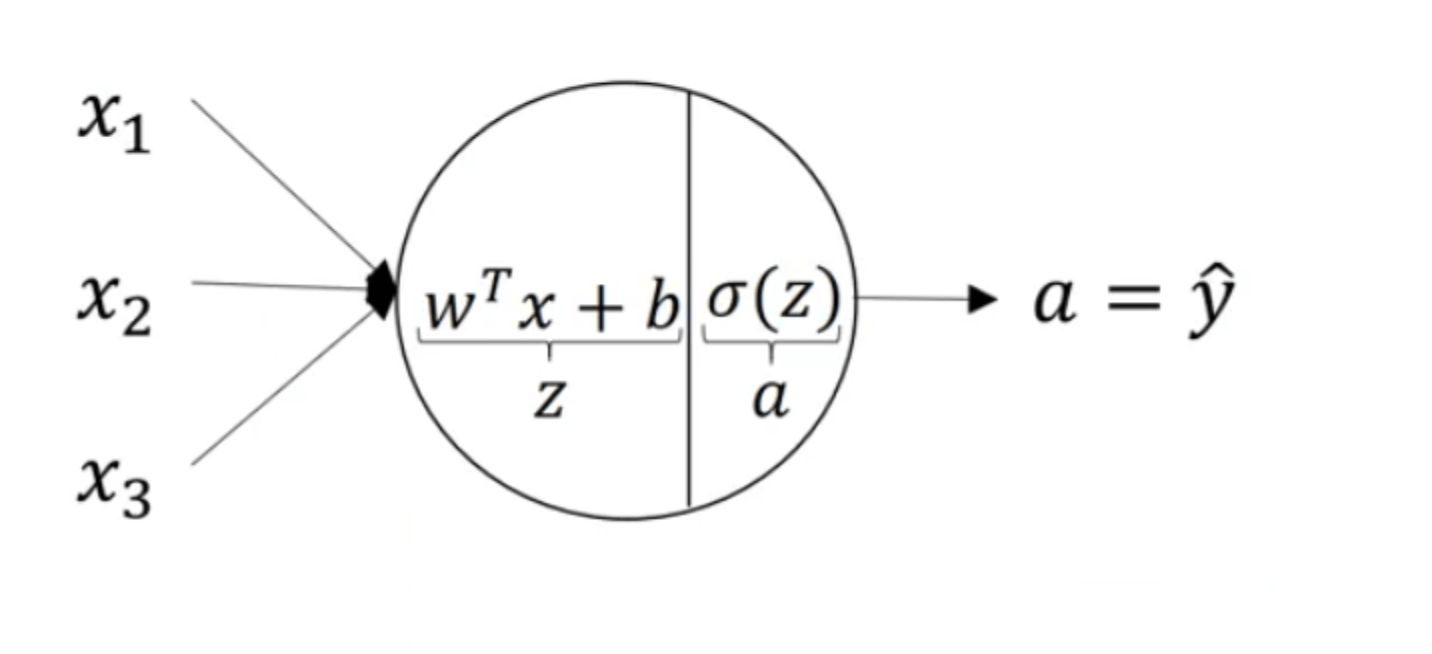
上图中的圆圈代表了逻辑回归计算的两个步骤。神经网络只不过是重复计算这些步骤很多次。
我们先来看隐藏层中的第一个神经元:
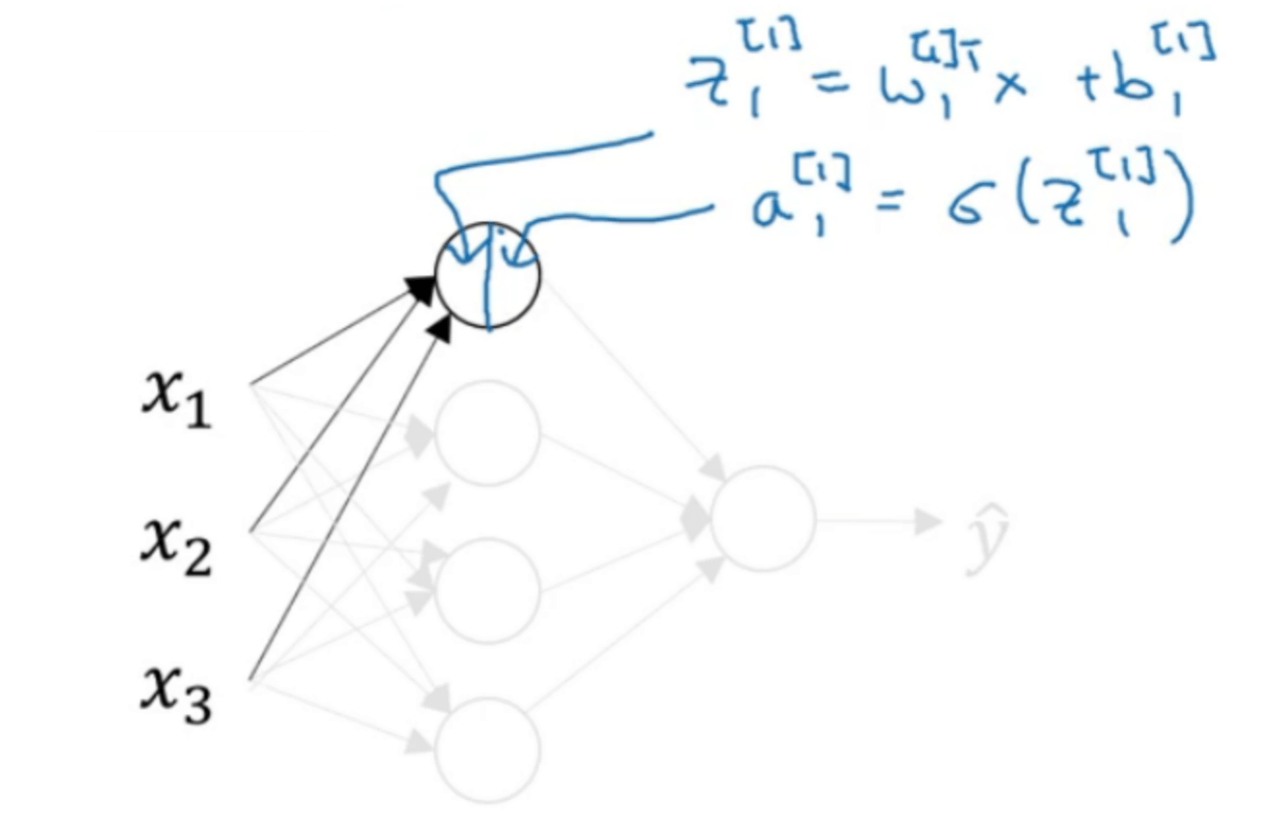
接下来是隐藏层的第二个神经元:
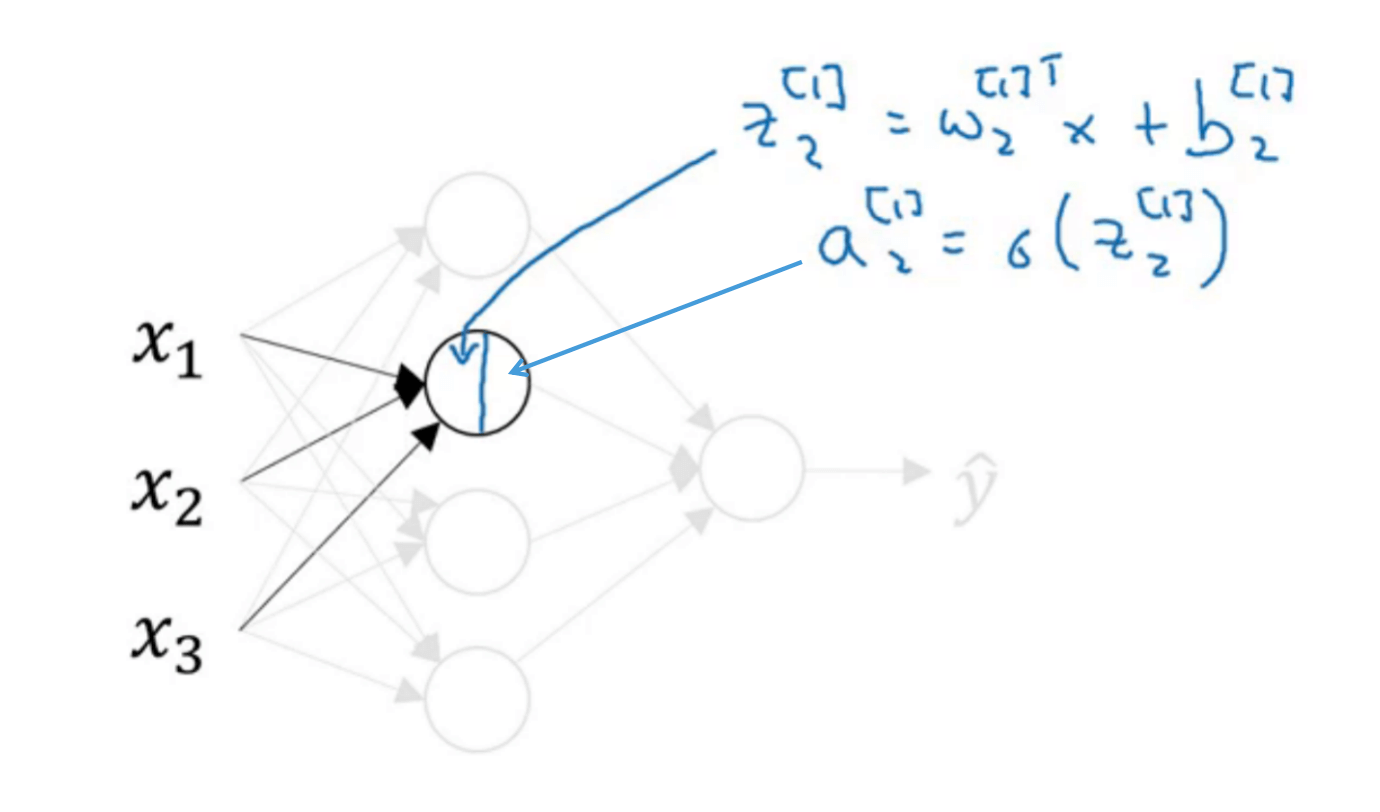
隐藏层的第三个和第四个神经元的计算类似,在此不再一一赘述:
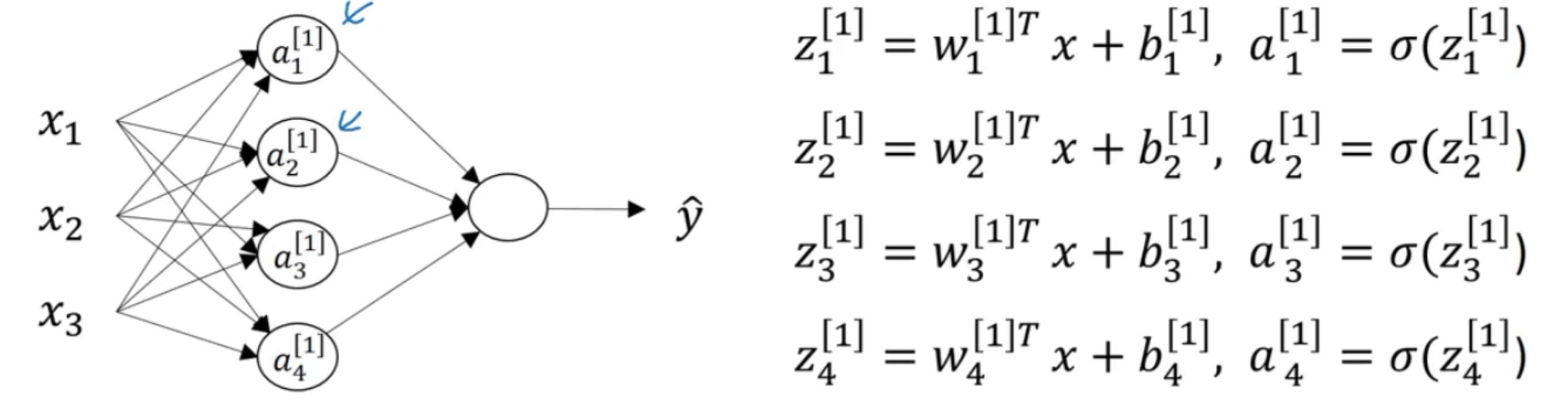
在计算隐藏层时,使用向量化技巧计算上述的四个式子:
\[\begin{bmatrix} z^{[1]}_1 \\ z^{[1]}_2 \\ z^{[1]}_3 \\ z^{[1]}_4 \\ \end{bmatrix} = \begin{bmatrix} \cdots {w^{[1]}_1}^T \cdots \\ \cdots {w^{[1]}_2}^T \cdots \\ \cdots {w^{[1]}_3}^T \cdots \\ \cdots {w^{[1]}_4}^T \cdots \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} +\begin{bmatrix} b^{[1]}_1 \\ b^{[1]}_2 \\ b^{[1]}_3 \\ b^{[1]}_4 \\ \end{bmatrix}\]可简化为:
\[z^{[1]}=W^{[1]} x+b^{[1]}\]以此类推,可得:
\[a^{[1]}=\begin{bmatrix} a^{[1]}_1 \\ a^{[1]}_2 \\ a^{[1]}_3 \\ a^{[1]}_4 \\ \end{bmatrix}=\sigma (z^{[1]})\]因此,第一个隐藏层的输出可由以下两步获得:
- $z^{[1]}=W^{[1]}x+b^{[1]}$
- 矩阵维度为:$(4\times 1)=(4\times 3)(3\times 1)+(4\times 1)$
- 因为$x=a^{[0]}$,所以上式也可写为$z^{[1]}=W^{[1]} a^{[0]}+b^{[1]}$
- $a^{[1]}=\sigma (z^{[1]})$
- 矩阵维度为:$(4\times 1)=\sigma ((4\times 1))$
用同样的方法可以推导下一层,即输出层的输出:
- $z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
- 矩阵维度为:$(1\times 1)=(1\times 4)(4\times 1)+(1\times 1)$
- $a^{[2]}=\sigma (z^{[2]})$
- 矩阵维度为:$(1\times 1)=\sigma ((1\times 1))$
3.多个例子中的向量化
在第2部分我们介绍了单个样本时计算神经网络的预测,在本节中我们将扩展到多个不同样本的情况。
如果使用显式的for循环完成这个操作:
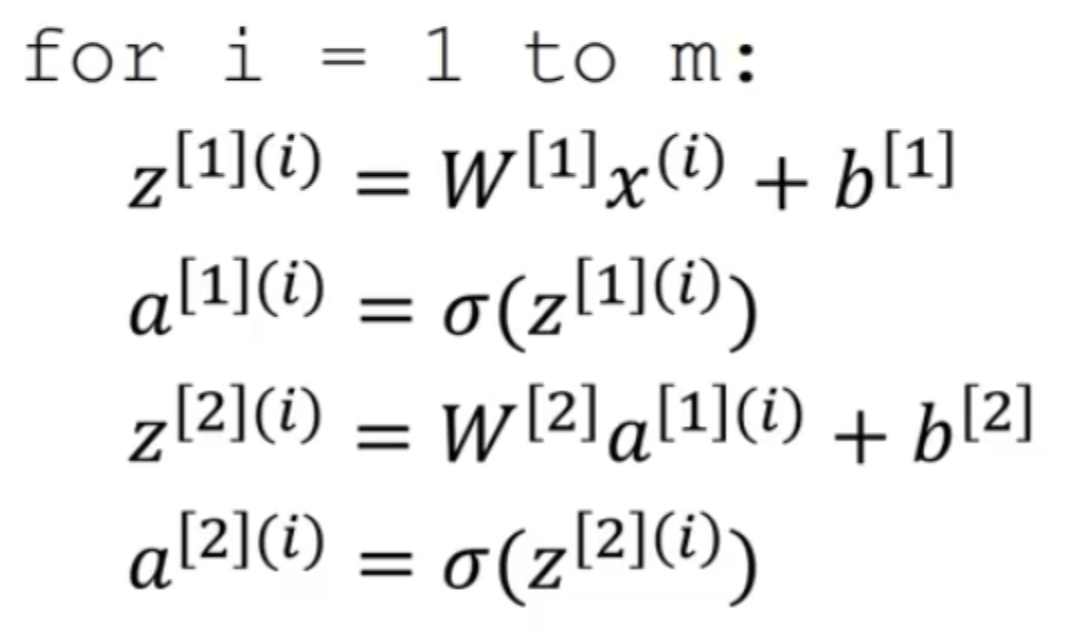
⚠️右上角的(i)表示第i个训练样本。
将其向量化:
- $Z^{[1]}=W^{[1]}X+b^{[1]}$,也可写为$Z^{[1]}=W^{[1]}A^{[0]}+b^{[1]}$
- $A^{[1]}=\sigma (Z^{[1]})$
- $Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]}$
- $A^{[2]}=\sigma ({Z^{[2]}})$
$X$的定义见【深度学习基础】第四课:正向传播与反向传播,有$X=A^{[0]}$。
其中,
\[Z^{[1]}=\begin{bmatrix} z^{[1](1)}_1 & z^{[1](2)}_1 & \cdots & z^{[1](m)}_1 \\ z^{[1](1)}_2 & z^{[1](2)}_2 & \cdots & z^{[1](m)}_2 \\ \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}\] \[A^{[1]}=\begin{bmatrix} a^{[1](1)}_1 & a^{[1](2)}_1 & \cdots & a^{[1](m)}_1 \\ a^{[1](1)}_2 & a^{[1](2)}_2 & \cdots & a^{[1](m)}_2 \\ \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}\]对于$Z^{[2]}$和$A^{[2]}$形式是一样的,不再赘述。