【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.前言
现实中常遇到多分类学习任务,通常有两种解决办法:
- 直接将二分类学习方法推广到多分类。
- 基于一些基本策略,利用二分类学习器解决多分类问题。
其中第2种方法更为常用,也是本文所要介绍的内容。
‼️不失一般性,考虑N个类别$C_1,C_2,…,C_N$,多分类学习的基本思路是“拆解法”,即将多分类任务拆为若干个二分类任务求解。通常可分为两步:
- 先对问题进行拆分,然后为拆出的每个二分类任务训练一个分类器。
- 在测试时,对这些分类器的预测结果进行集成以获得最终的多分类结果。
本文主要介绍拆分策略。
最经典的拆分策略有三种:
- “一对一”(One vs. One,简称OvO)。
- “一对其余”(One vs. Rest,简称OvR)。
- “多对多”(Many vs. Many,简称MvM)。
OvR亦称OvA(One vs. All),但是OvA这个说法不严格,因为不可能把“所有类”作为反类。
2.OvO
给定数据集$D=\{ (\mathbf x_1,y_1), (\mathbf x_2,y_2), … , (\mathbf x_m,y_m) \},y_i \in \{ C_1,C_2, … ,C_N \}$。OvO将这N个类别两两配对,从而产生N(N-1)/2个二分类任务。最终结果可通过投票产生:即把被预测得最多的类别作为最终分类结果。
亦可根据各分类器的预测置信度等信息进行集成。
3.OvR
OvR则是每次将一个类的样例作为正例、所有其他类的样例作为反例来训练N个分类器。
- 在测试时若仅有一个分类器预测为正类,则对应的类别标记作为最终分类结果。
- 若有多个分类器预测为正类,则通常考虑各分类器的预测置信度,选择置信度最大的类别作为分类结果。
👉OvO与OvR示意图:
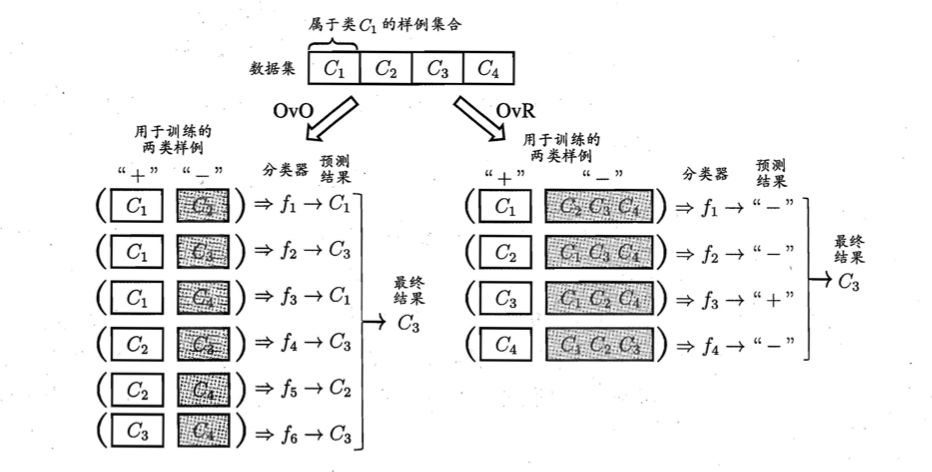
容易看出,OvR只需训练N个分类器,而OvO需训练N(N-1)/2个分类器,因此,OvO的存储开销和测试时间开销通常比OvR更大。
⚠️但在训练时,OvR的每个分类器均使用全部训练样例,而OvO的每个分类器仅用到两个类的样例,因此,在类别很多时,OvO的训练时间开销通常比OvR更小。
至于预测性能,则取决于具体的数据分布,在多数情况下两者差不多。
4.MvM
MvM是每次将若干个类作为正类,若干个其他类作为反类。显然,OvO和OvR是MvM的特例。
⚠️MvM的正、反类构造必须有特殊的设计,不能随意选取。
这里我们介绍一种最常用的MvM技术:“纠错输出码”(Error Correcting Output Codes,简称ECOC)。
4.1.纠错输出码
ECOC的工作过程分为两步:
- 编码:对N个类别做M次划分,每次划分将一部分类别划为正类,一部分划为反类,从而形成一个二分类训练集;这样一共产生M个训练集,可训练出M个分类器。
- 解码:M个分类器分别对测试样本进行预测,这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测结果。
⚠️类别划分通过“编码矩阵”指定。编码矩阵有多种形式,常见的主要有二元码和三元码。前者将每个类别分别指定为正类和反类,后者在正、反类之外,还可指定“停用类”。
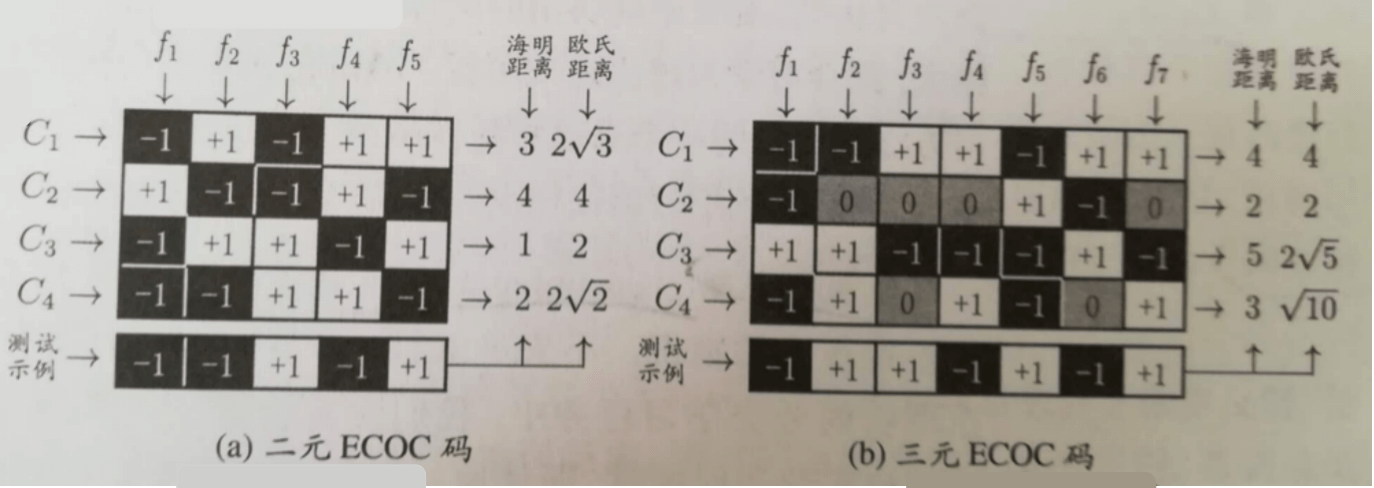
在ECOC编码示意图中,“+1”、“-1”分别表示学习器$f_i$将该类样本作为正、反例;三元码中“0”表示$f_i$不使用该类样本。
海明距离:
在信息编码中,两个合法代码对应位上编码不同的位数称为码距,又称海明距离。
举例如下:
10101和00110从第一位开始依次有第一位、第四位和第五位不同,则海明距离为3。
为什么称为“纠错输出码”呢?
这是因为在测试阶段,ECOC编码对分类器的错误有一定的容忍和修正能力。例如上图(a)中,对测试示例的正确预测为类$C_3$,即编码为(-1,+1,+1,-1,+1),假设在预测时某个分类器出错了,例如$f_2$出错从而导致了错误编码(-1,-1,+1,-1,+1),但基于这个编码仍能产生正确的最终分类结果$C_3$。
⚠️在三元码中,对于“0”,即学习器没有使用的类别,海明距离记为0.5。
‼️一般来说,对同一个学习任务,ECOC编码越长,纠错能力越强。然而,编码越长,意味着所需训练的分类器越多,计算、存储开销都会增大;另一方面,对有限类别数,可能的组合数目是有限的,码长超过一定范围后就失去了意义。