【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.神经网络的梯度下降法
在【深度学习基础】第四课:正向传播与反向传播一文中我们了解了反向传播的原理,学习了梯度下降法在logistic回归中的应用。其实,logistic回归模型就可以看作是一个没有隐藏层的神经网络结构。那么,梯度下降法在一个带有隐藏层的浅层神经网络中是怎么应用的呢?这便是本文所要讨论的内容。
我们以【深度学习基础】第六课:浅层神经网络中所用的双层神经网络为例:
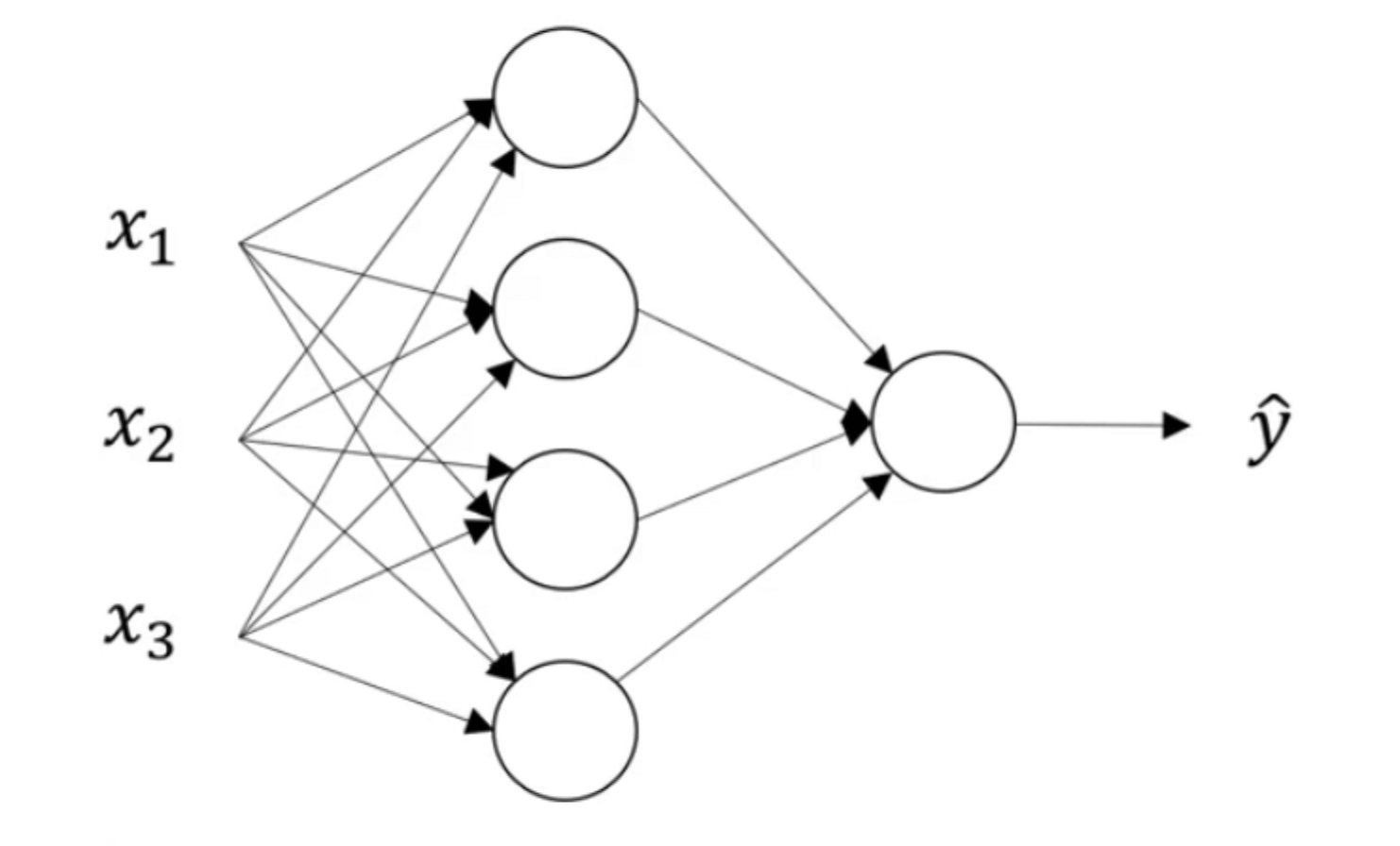
假设所有激活函数均为sigmoid函数,所要解决的问题为二分类问题。loss function和cost function依然采用交叉熵损失函数。
1.1.单样本的情况
首先,我们先考虑只有一个样本的情况。
在反向传播之前,我们先复习下正向传播的过程。假设样本的维数为m,即有m个特征。则我们的输入为:
\[x=a^{[0]}=\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_m \\ \end{bmatrix} _{m \times 1}\]第一层(即隐藏层)的参数$w^{[1]}$和$b^{[1]}$分别为:
\[w^{[1]}=\begin{bmatrix} \cdots & {w^{[1]}_1}^T & \cdots \\ \cdots & {w^{[1]}_2}^T & \cdots \\ \cdots & {w^{[1]}_3}^T & \cdots \\ \cdots & {w^{[1]}_4}^T & \cdots \\ \end{bmatrix}_{4\times m}\] \[b^{[1]}=\begin{bmatrix} b^{[1]}_1 \\ b^{[1]}_2 \\ b^{[1]}_3 \\ b^{[1]}_4 \\ \end{bmatrix}_{4\times 1}\]据此可得到第一层的输出$a^{[1]}$为:
\[a^{[1]}=\begin{bmatrix} a^{[1]}_1 \\ a^{[1]}_2 \\ a^{[1]}_3 \\ a^{[1]}_4 \\ \end{bmatrix}_{4\times 1}=\sigma (z^{[1]})=\sigma (\begin{bmatrix} z^{[1]}_1 \\ z^{[1]}_2 \\ z^{[1]}_3 \\ z^{[1]}_4 \\ \end{bmatrix}_{4\times 1} )\]第二层的参数$w^{[2]}$和$b^{[2]}$为:
\[w^{[2]}=\begin{bmatrix} \cdots & {w^{[2]}_1}^T & \cdots \\ \end{bmatrix}_{1\times 4}\] \[b^{[2]}=\begin{bmatrix} b^{[2]}_1 \end{bmatrix}_{1\times 1}\]第二层的输出$a^{[2]}$为:
\[a^{[2]}=\begin{bmatrix} a^{[2]}_1 \end{bmatrix}_{1\times 1}=\sigma (z^{[2]})=\sigma (\begin{bmatrix} z^{[2]}_1 \end{bmatrix}_{1\times 1})\]借用【深度学习基础】第四课:正向传播与反向传播中计算的导数的结果,我们通过反向传播可以很快得到:
- $da^{[2]}=-\frac{y}{a^{[2]}}+\frac{1-y}{1-a^{[2]}}$;维数为$1\times 1$。
- $dz^{[2]}=a^{[2]}-y$;维数为$1\times 1$。
- $dw^{[2]}=dz^{[2]}{a^{[1]}}^T$;维数为$1\times 4=(1\times 1)(1\times 4)$。
- $db^{[2]}=dz^{[2]}$;维数为$1\times 1$。
- $da^{[1]}=dz^{[2]}{w^{[2]}}^T$;维数为$4\times 1$。
- $dz^{[1]}=da^{[1]} * g^{[1]’}(z^{[1]})$;维数为$4\times 1$。
*表示$da^{[1]}$中的每个元素都乘上$g^{[1]’}(z^{[1]})$。其中,$g^{[1]’}(z^{[1]})=a^{[1]}(1-a^{[1]})$。 - $dw^{[1]}=dz^{[1]}{a^{[0]}}^T$;维度为$4\times m=(4\times 1)(1\times m)$。
- $db^{[1]}=dz^{[1]}$;维度为$4\times 1$。
1.2.多个样本的情况
n个样本的情况和单样本基本类似:
- $dZ^{[2]}=A^{[2]}-Y$;维度为$1\times n$。
- $dw^{[2]}=\frac{1}{n} dZ^{[2]}{A^{[1]}}^T$;维数为$1\times 4=(1\times n)(n \times 4)$。
- $db^{[2]}=\frac{1}{n} np.sum(dZ^{[2]},axis=1,keepdims=True)$;维度为$1\times 1$。
- $dZ^{[1]}=dA^{[1]}*g^{[1]’}(Z^{[1]})$;维数为$4\times n$。
- $dw^{[1]}=\frac{1}{n} dZ^{[1]} {A^{[0]}}^T$;维数为$4\times m=(4\times n)(n \times m)$。
- $db^{[1]}=\frac{1}{n} np.sum(dZ^{[1]},axis=1,keepdims=True)$;维数为$4\times 1$。
2.网络参数的随机初始化
‼️如果将神经网络的各参数数组全部初始化为0,会使得梯度下降算法完全无效。
👉但是如果只是逻辑回归的话,可以将所有参数都初始化为0。
假设我们有如下的逻辑回归模型:

正向传播:
- $a_1=sigmoid(w_{11}x_1+w_{21}x_2+b)$
- $L=-ylog(a_1)-(1-y)log(1-a_1)$
反向传播:
- $da_1=-\frac{y}{a_1}+\frac{1-y}{1-a_1}$
- $dw_{11}=(a_1-y)x_1$
- $dw_{21}=(a_1-y)x_2$
- $db=(a_1-y)$
当$w_{11}=w_{21}=0$时,$dw_{11}$和$dw_{21}$会因为$x_1$和$x_2$的不同而不同,梯度下降法可以正常进行。即使b也等于0,梯度下降法依旧可以正常进行。
👉现在考虑神经网络中的所有参数被初始化为0的情况。
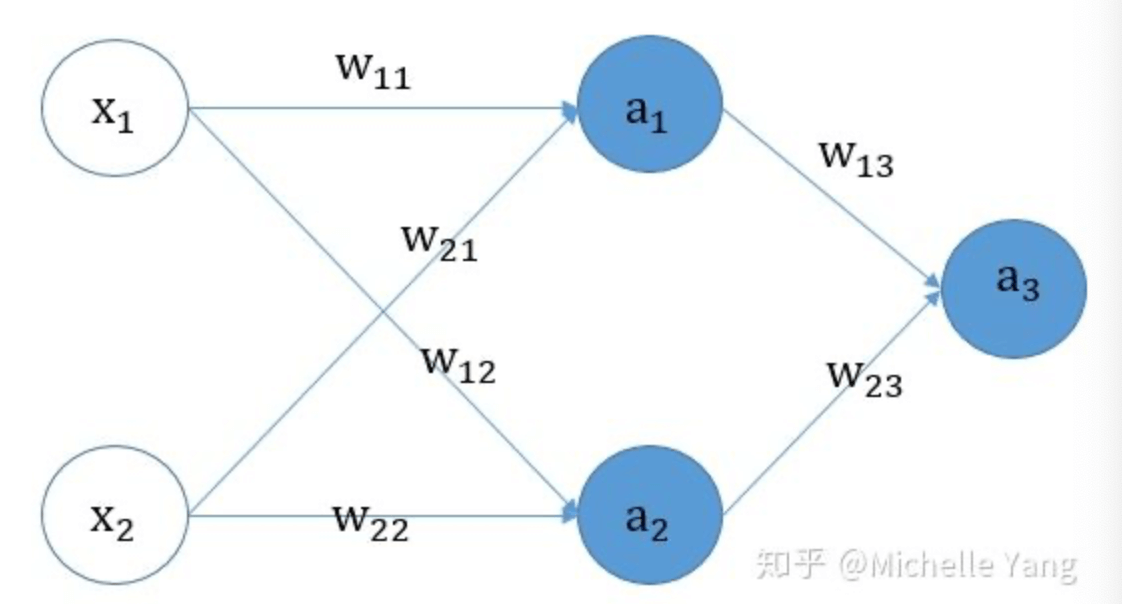
正向传播:
- $a_1=g(w_{11}x_1+w_{21}x_2+b_1)$
- $a_2=g(w_{12}x_1+w_{22}x_2+b_2)$
- $a_3=sigmoid(w_{13}a_1+w_{23}a_2+b_3)$
- $L=-ylog a_3-(1-y)log(1-a_3)$
反向传播:
- $da_3=-\frac{y}{a_3}+\frac{1-y}{1-a_3}$
- $dw_{13}=(a_3-y)a_1$
- $dw_{23}=(a_3-y)a_2$
- $db_3=(a_3-y)$
- $da_1=(a_3-y)w_{13}$
- $da_2=(a_3-y)w_{23}$
- $dw_{12}=da_2*a_2’*x_1$
- $dw_{22}=da_2*a_2’*x_2$
- $db_2=da_2*a_2’$
- $dw_{11}=da_1*a_1’*x_1$
- $dw_{21}=da_1*a_1’*x_2$
- $db_1=da_1*a_1’$
我们考虑以下两种情况:
✓情况一:模型所有权重w初始化为0,所有偏置b初始化为0。
始终有$a_1=a_2=g(0)$,所以始终有$dw_{13}=dw_{23}$,每次迭代更新权重时,$w_{13}$总是等于$w_{23}$,出现权重的对称性。
在第一次迭代时,因为$w_{13}=w_{23}=0$,所以$da_1=da_2=0$,所以$dw_{12}=dw_{22}=dw_{11}=dw_{21}=0$,因此在第一次梯度下降法运行时,除了$w_{13}$和$w_{23}$能够及时得到更新,其余权重均得不到更新。在之后的迭代中,因为$w_{13}$和$w_{23}$总是相等,所以始终有$dw_{12}=dw_{11};dw_{22}=dw_{21}$,即始终有$w_{12}=w_{11};w_{22}=w_{21}$,也呈现出权重的对称性。
这样使得同一隐藏层内的多个神经元完全在运行相同的操作(一样的输入和输出),没有任何意义。
✓情况二:模型所有权重w初始化为0,所有偏置b随机初始化。
因为b的随机初始化,所以$a_1\neq a_2$,所以$w_{13}$和$w_{23}$可以正常更新。
$w_{11},w_{12},w_{21},w_{22}$除了第一次迭代无法更新,后续迭代也可以正常更新。
并且均不存在权重对称性。
但是这种方式存在更新较慢,梯度消失,梯度爆炸等问题,在实践中,通常不会选择此方式。
因此,我们常用的解决办法就是:随机初始化网络参数。例如产生高斯分布随机变量:
\[w^{[1]}=np.random.randn((2,2))*0.01\]一般还会在末尾乘上一个很小的数字,例如0.01, 将权重初始化成很小的随机数。
因为如果权重初始值很大,对于sigmoid和tanh函数,计算得到的z值就会很大或很小,这样就会使梯度变得很小,梯度下降法的收敛速度会非常慢。 但是如果我们的神经网络中没有sigmoid或tanh函数,那么可能影响就不会很大。
在训练浅层神经网络时,0.01通常是一个比较合适的值。但是当训练深层神经网络时,一般会选择一个其他的常数,这个在今后的博客中会有介绍。
但是参数$b$可以初始化为0,这个是没有影响的:
\[b^{[1]}=np.zero((2,1))\]