【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章，未经本人允许，禁止转载。转载请注明出处。

1.前言

梯度检验（gradient checking）的作用是确保反向传播的正确实施。

为了逐渐实现梯度检验，我们首先了解下如何对梯度做数值逼近。

2.梯度的数值逼近

假设我们有函数$f(\theta)=\theta ^3$，图像见下：

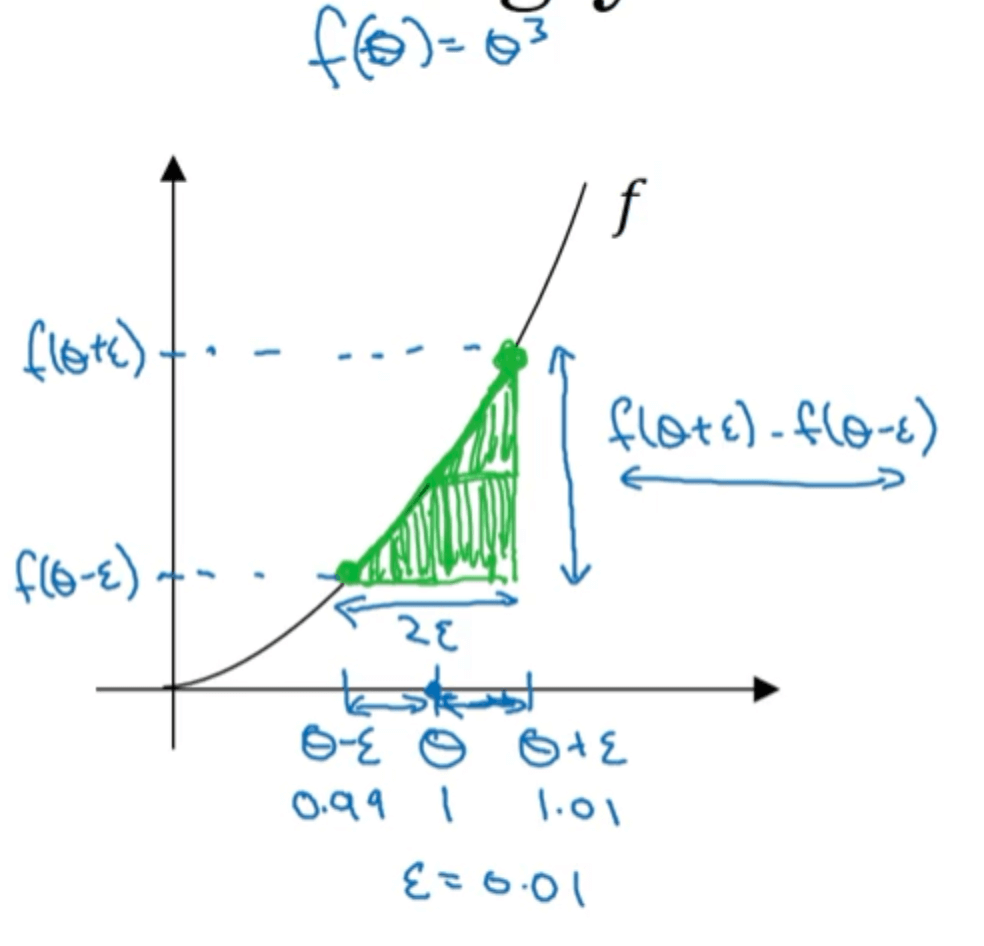
如图所示，假设我们考虑$\theta=1$时的导数并且有一个很小的值$\epsilon=0.01$。

如果使用单边误差估计导数：

\[\frac{f(\theta+\epsilon)-f(\theta)}{\epsilon}=\frac{1.01^3-1}{0.01}=3.0301\]

如果使用双边误差估计导数：

\[\frac{f(\theta+\epsilon)-f(\theta-\epsilon)}{2\epsilon}=\frac{1.01^3-0.99^3}{2\times 0.01}=3.0001\]

$\theta=1$时，函数的导数为：

\[f'(\theta)=3\theta ^2=3\]

很明显，双边误差对导数的估计更加准确。这是因为单边估计时误差为$O(\epsilon)$，而双边估计时误差为$O(\epsilon ^2)$，当$\epsilon <1$时，肯定有$\epsilon ^2 < \epsilon$，因此双边估计比单边估计更为准确。

⚠️我们在做梯度检验时就会用到双边误差公式。

把神经网络的所有参数：$W^{[1]},b^{[1]},…,W^{[L]},b^{[L]}$合成一个大的向量$\theta$。

同样的，把$dW^{[1]},db^{[1]},…,dW^{[L]},db^{[L]}$也合成一个大的向量$d\theta$。

其中，$\theta$和$d\theta$的维度是完全一样的。

cost function为：

\[J(W^{[1]},b^{[1]},...,W^{[L]},b^{[L]})=J(\theta_1,\theta_2,...)=J(\theta)\]

利用第2部分介绍的双边误差公式，计算每一个$\theta_i$的导数近似值：

\[d\theta_{approx}[i]=\frac{J(\theta_1,\theta_2,...,\theta_i+\epsilon,...)-J(\theta_1,\theta_2,...,\theta_i-\epsilon,...)}{2\epsilon}\]

如果后向传播正确的话，我们得到的$d\theta_{approx}[i]$应该是接近于$d\theta [i]$的。总体看来，也就是两个大的向量：$d\theta_{approx}$和$d\theta$之间应该是接近的。

采用以下公式计算$d\theta_{approx}$和$d\theta$之间的接近程度：

\[\frac{\parallel d\theta_{approx} - d\theta \parallel _2}{\parallel d\theta_{approx} \parallel _2+\parallel d\theta \parallel _2} \approx \epsilon\]

其实就是计算欧式距离并做了归一化处理。通常$\epsilon = 10^{-7}$。如果计算得到的值远远大于$10^{-7}$，那很有可能就是反向传播的时候出现了错误。但这并不是绝对的，也有可能没有错误，这只是意味着出现错误的可能性很大。