本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.图像模糊
图像模糊是图像处理中最简单和常用的操作之一。
⚠️使用该操作的原因之一是为了给图像预处理时降低噪声。
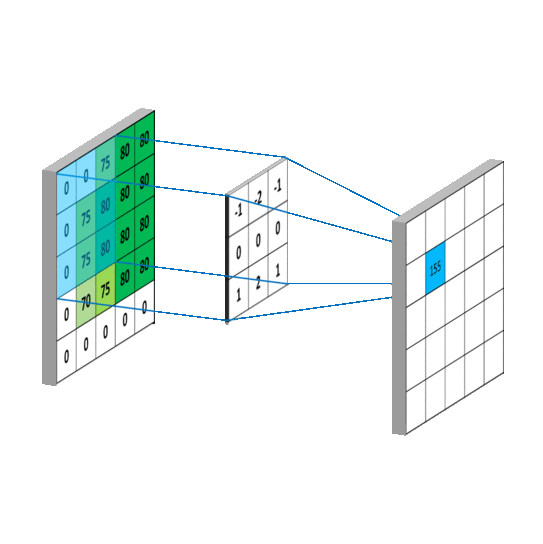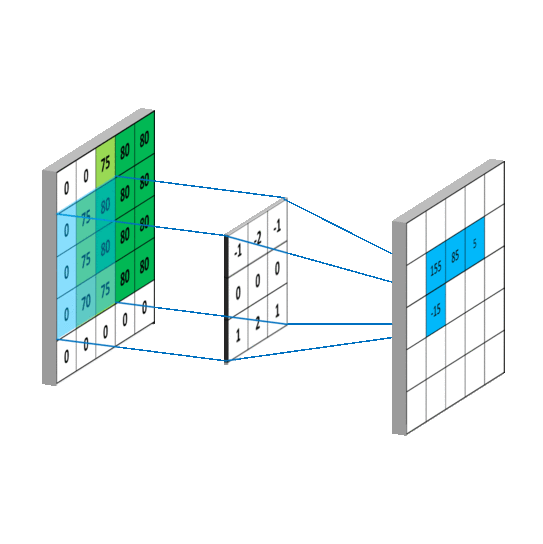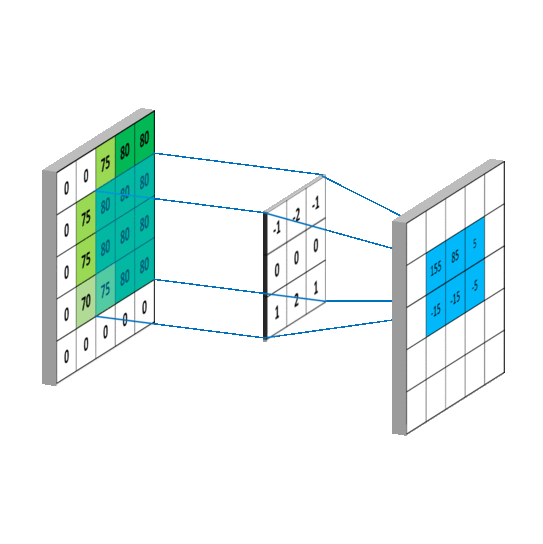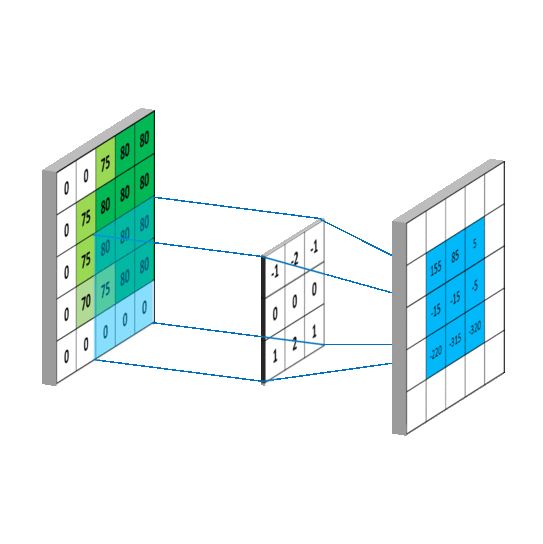
图像模糊操作背后是数学的卷积计算。
卷积操作的原理:
常用的图像模糊的方法:
- 均值模糊
- 高斯模糊
- 中值模糊
- 双边模糊
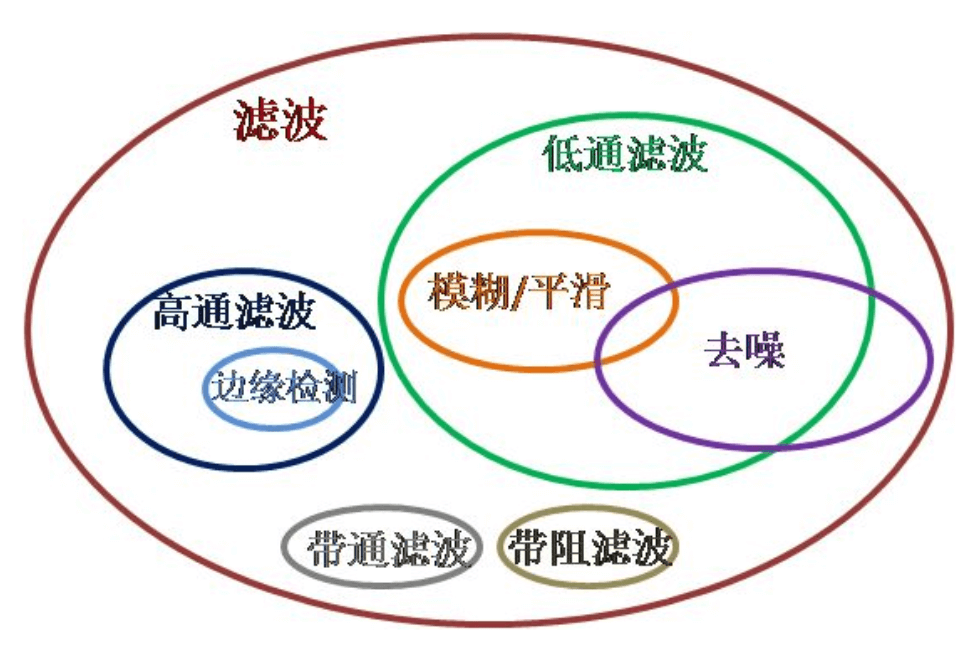
这四种模糊方式有时也被称为:均值滤波、高斯滤波、中值滤波和双边滤波。因为模糊属于一种滤波操作,具体关系可参照下图:
其中,均值滤波、高斯滤波和中值滤波属于线性滤波;而双边滤波属于非线性滤波。
接下来我们结合OpenCV中的相关API来进一步了解这些图像模糊的方法。
2.均值模糊
均值模糊的卷积核为:
\[kernel=\frac{1}{kernel_{width}\times kernel_{height}} \begin{bmatrix} 1 & \cdots & 1 \\ \vdots & \ddots & \vdots \\ 1 & \cdots & 1 \\ \end{bmatrix}\]卷积核亦称掩膜。
OpenCV中的API:
1
2
3
4
5
6
7
void blur(
InputArray src,
OutputArray dst,
Size ksize,
Point anchor=Point(-1,-1),
int borderType = BORDER_DEFAULT
);
部分参数解释:
- 参数
Size ksize表示卷积核的大小。Size(3,3)表示$3\times 3$的核大小;Size(5,5)表示$5\times 5$的核大小。边长必须是正奇数。 - 参数
Point anchor表示锚点(anchor)的位置,即被平滑的那个点。默认值Point(-1,-1)表示锚点位于核的中心。
现在我们看下原图进行均值模糊之后的结果(左侧为原图,右侧为均值模糊后的图):
1
blur(src,src_blur,Size(5,5),Point(-1,-1));

3.高斯模糊
3.1.高斯模糊的原理
高斯模糊所用的卷积核就是基于二维高斯分布生成的。
二维高斯分布见本文第6部分。
在高斯模糊中,二维高斯分布公式中的$x_1,x_2$对应一个点的x,y坐标。因此可以假设$x_1,x_2$是相互独立的,所以:
\[Cov(x_1,x_2)=Cov(x_2,x_1)=E(x_1x_2)-E(x_1)E(x_2)=E(x_1)E(x_2)-E(x_1)E(x_2)=0\]并且:
\[Cov(x_1,x_1)=E(x_1^2)-E^2(x_1)=\sigma_1^2\]同理:
\[Cov(x_2,x_2)=\sigma_2^2\]代入协方差矩阵$\sum$:
\[\sum=\begin{bmatrix} Cov(x_1,x_1) & Cov(x_1,x_2) \\ Cov(x_2,x_1) & Cov(x_2,x_2) \\ \end{bmatrix}=\begin{bmatrix} \sigma_1^2 & 0 \\ 0 & \sigma_2^2 \end{bmatrix}\]求其行列式:
\[\mid \sum \mid=\sigma_1^2 \sigma_2^2\]则二维高斯分布公式可简化为:
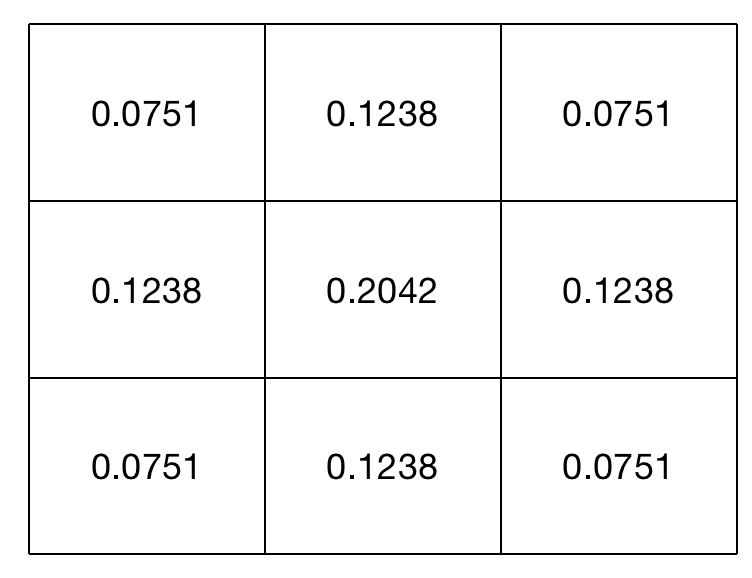
\[f(\bar x)=\frac{1}{(2\pi)(\sigma_1^2 \sigma_2^2)^{1/2} } e^{-\frac{1}{2}[(\frac{x_1-\mu_1}{\sigma_1})^2 + (\frac{x_2-\mu_2}{\sigma_2})^2]}\]假设我们要生成一个$3\times 3$的高斯掩膜,锚点的坐标设置为(0,0),则周边点的坐标为:
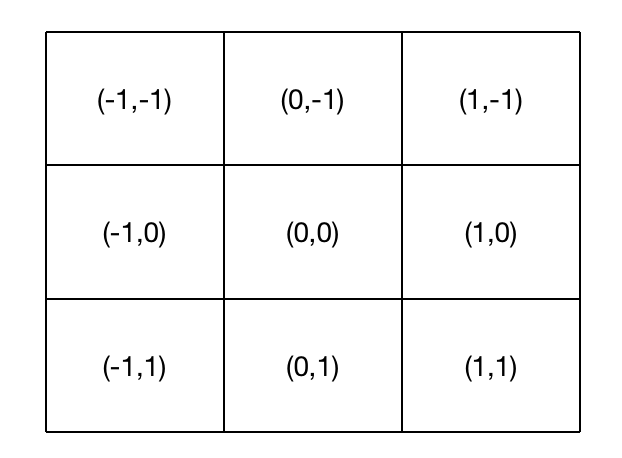
将$(x_1,x_2)$对应的值代入上述公式中即可求得高斯掩膜。
为了方便,我们这里假设$\mu_1=\mu_2=0,\sigma_1=\sigma_2=1$,又因为系数$\frac{1}{2\pi}$为常数,因此可以省略,将二维高斯分布公式简化为:
\[e^{-\frac{1}{2}(x_1^2+x_2^2)}\]据此可得到:
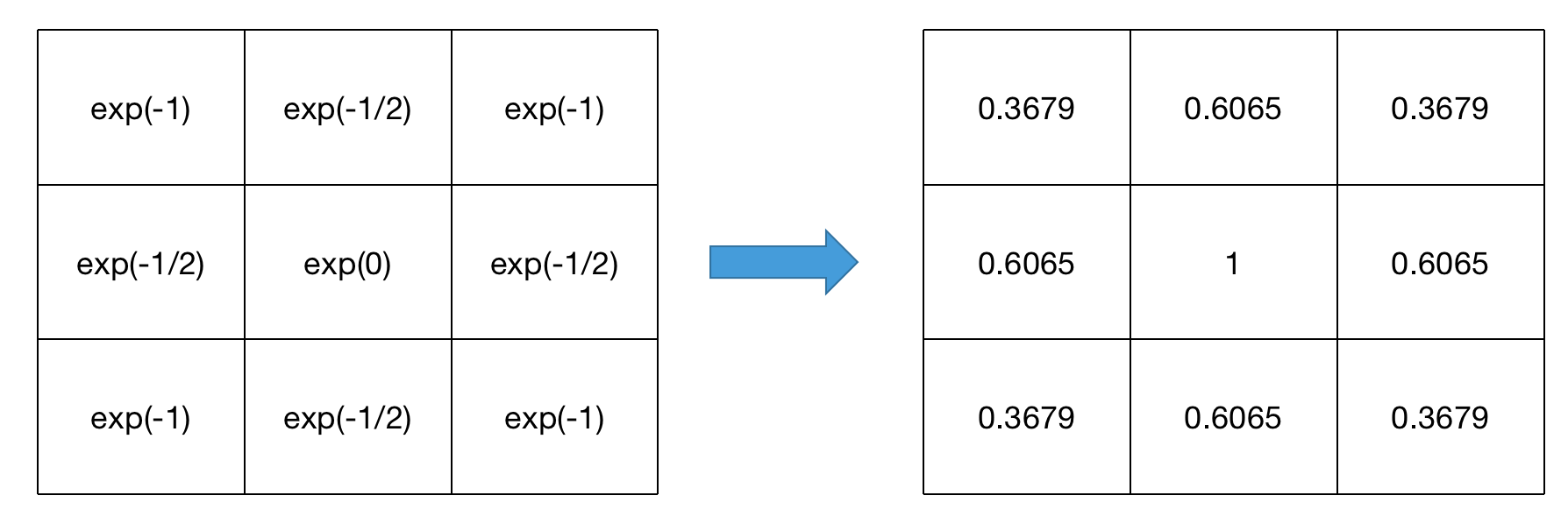
这9个点的权重总和不等于1,所以需要对其进行归一化处理:每个格子的数除以所有格子的数加起来的总和。这样即可得到一个$3\times 3$的高斯掩膜:
3.2.高斯模糊的API
1
2
3
4
5
6
7
8
void GaussianBlur(
InputArray src,
OutputArray dst,
Size ksize,
double sigmaX,
double sigmaY = 0,
int borderType = BORDER_DEFAULT
);
其中,参数Size ksize表示卷积核的大小。sigmaX(高斯核在x方向的标准差)和sigmaY(高斯核在y方向的标准差)对应二维高斯分布公式中的$\sigma_1,\sigma_2$。
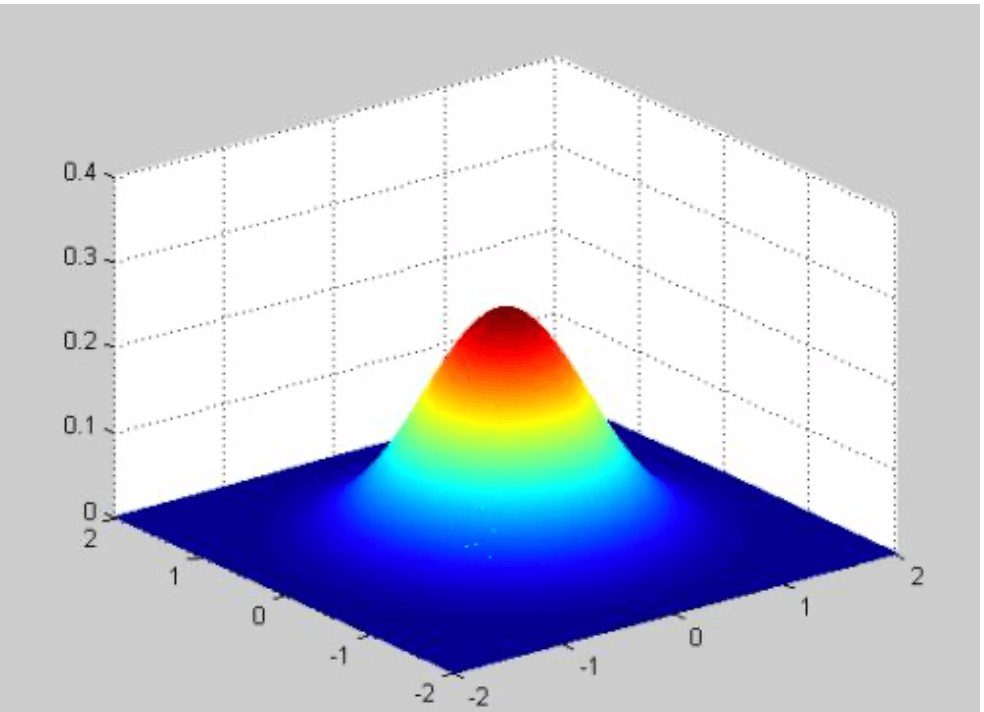
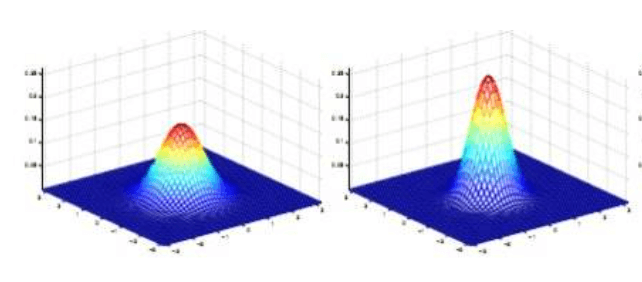
如果$\sigma$较小(其二维高斯分布概率密度函数图像见下图右),那么生成的掩膜的中心系数较大,而周围的系数较小,这样对图像的模糊效果就不是很明显;反之,$\sigma$较大(其二维高斯分布概率密度函数图像见下图左),则生成的模版的各个系数相差就不是很大,比较类似均值模糊,对图像的模糊效果比较明显。
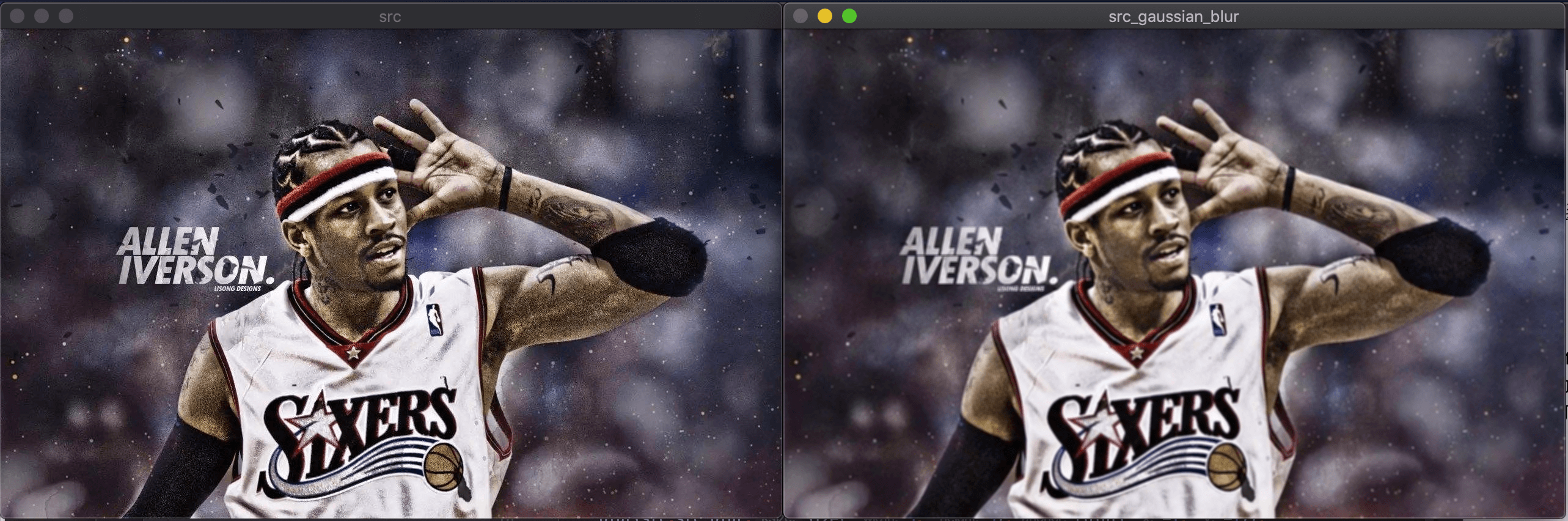
实际应用看下对比效果(左侧为原图,右侧为高斯模糊后的图):
1
GaussianBlur(src,src_gaussian_blur,Size(5,5),3,3);
4.中值模糊
中值模糊即用中位数填补中心像素。
中值滤波的扩展:最小值滤波、最大值滤波。
中值模糊对椒盐噪声有很好的抑制作用。
椒盐噪声:也称为脉冲噪声,是图像中经常见到的一种噪声,它是一种随机出现的白点或者黑点,也可能是亮的区域有黑色像素或是在暗的区域有白色像素(或者两者皆有)。
中值模糊的API:
1
2
3
4
5
void medianBlur(
InputArray src,
OutputArray dst,
int ksize
);
参数int ksize表示核的大小,必须大于1而且必须是奇数。
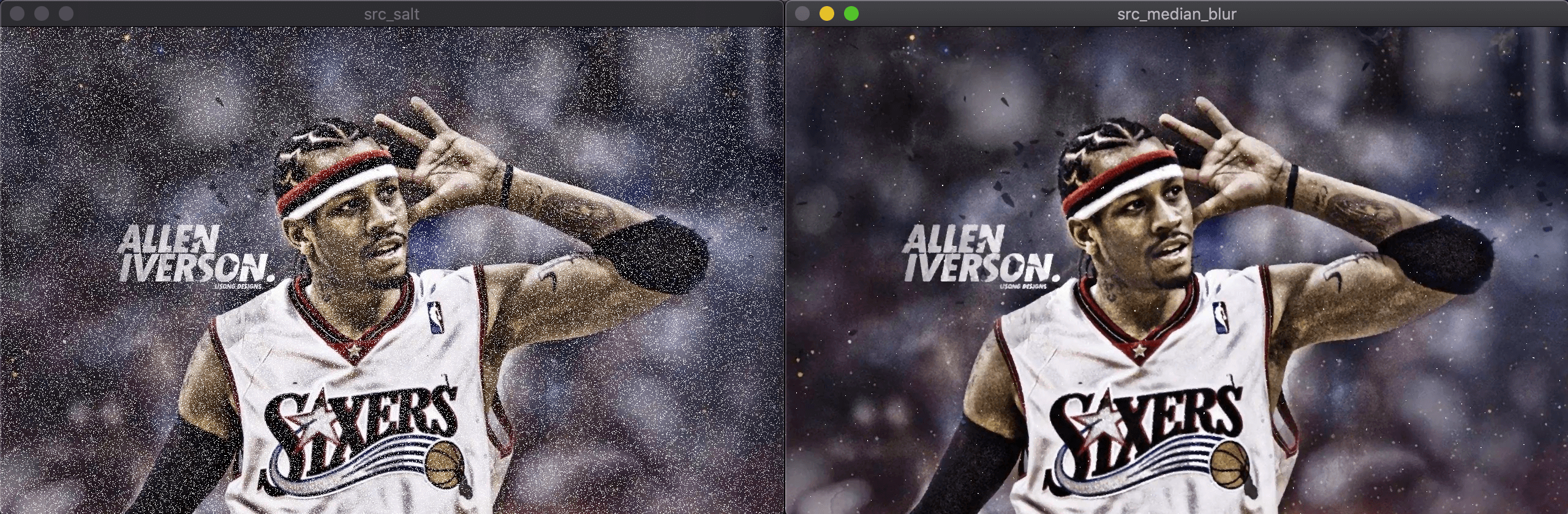
结果对比见下(左侧为加了椒盐噪声的原图,右侧为中值模糊后的图):
1
medianBlur(src_salt,src_median_blur,3);
5.双边模糊
均值模糊无法克服边缘像素信息丢失缺陷,原因是均值滤波是基于平均权重。
高斯模糊部分克服了该缺陷,但是无法避免,因为没有考虑像素值的不同。
高斯双边模糊是边缘保留的滤波方法,避免了边缘信息丢失,保留了图像轮廓不变(边缘指的是物体的边缘、轮廓)。
5.1.双边模糊的原理
⚠️双边滤波器综合了高斯滤波器和$\alpha$截尾均值滤波器的特点。高斯滤波器只考虑像素间的欧式距离,其使用的模版系数随着和窗口中心的距离增大而减小;$\alpha$截尾均值滤波器则只考虑了像素灰度值之间的差值,去掉$\alpha$%的最小值和最大值后再计算均值。
‼️双边滤波器就等于空间距离与灰度距离的乘积。其使用二维高斯函数生成距离模版,使用一维高斯函数生成值域模版(以下公式都省去了前面的系数)。
👉距离模版系数的生成公式如下:
\[d(i,j,k,l)=exp(-\frac{(i-k)^2+(j-l)^2}{2\sigma_d^2})\]这个公式和3.1部分中的公式其实是一样的。只不过省去了系数,并且假定$\sigma_1=\sigma_2=\sigma_d$。$(k,l)$为模版窗口的中心坐标,通常为(0,0),也就是$(\mu_1,\mu_2)$。$(i,j)$为模版窗口的其他系数的坐标,即$(x_1,x_2)$。
👉值域模版系数的生成公式如下:
\[r(i,j,k,l)=exp(-\frac{\parallel f(i,j)-f(k,l) \parallel ^2}{2\sigma_r^2})\]其中,$f(x,y)$表示图像在点$(x,y)$处的像素值;$(k,l)$为模版窗口的中心坐标;$(i,j)$为模版窗口的其他系数的坐标;$\sigma_r^2$为高斯函数的方差。
将上述两个模版相乘就得到了双边滤波器的模版:
\[w(i,j,k,l)=d(i,j,k,l)*r(i,j,k,l)=exp(-\frac{(i-k)^2+(j-l)^2}{2\sigma_d^2} -\frac{\parallel f(i,j)-f(k,l) \parallel ^2}{2\sigma_r^2})\]双边滤波也可以用下图表示,对P点进行模糊,Q点的距离虽然很近,但是像素值差距过大,所以Q点的权重很小,不会过多的考虑到Q点的信息,所以说双边滤波考虑到了边缘信息,避免了边缘信息的丢失。
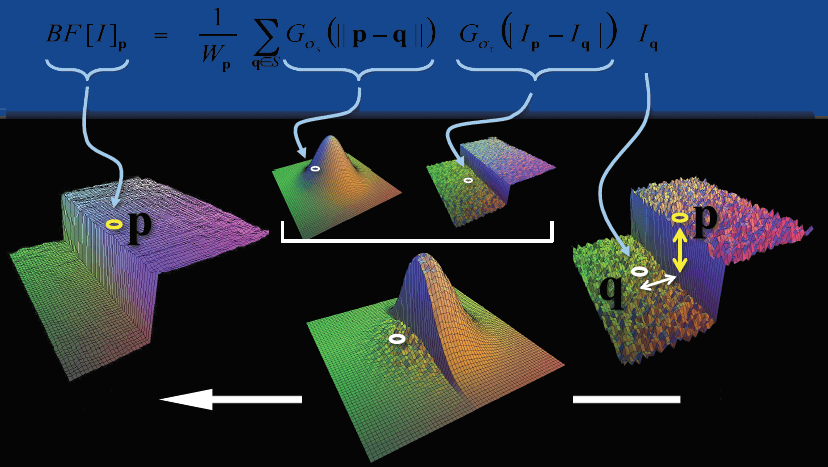
5.2.双边模糊的API
1
2
3
4
5
6
7
8
void bilateralFilter(
InputArray src,
OutputArray dst,
int d,
double sigmaColor,
double sigmaSpace,
int borderType=BORDER_DEFAULT
);
部分参数解释:
int d是计算直径,范围内的像素都会被纳入计算。如果这个值我们设其为非正数,那么OpenCV会从第五个参数sigmaSpace来计算出它来。double sigmaColor即为公式中的$\sigma_r$。这个参数的值越大,就表明该像素邻域内有更宽广的颜色会被混合到一起。double sigmaSpace即为公式中的$\sigma_d$。数值越大,意味着越远的像素会相互影响。
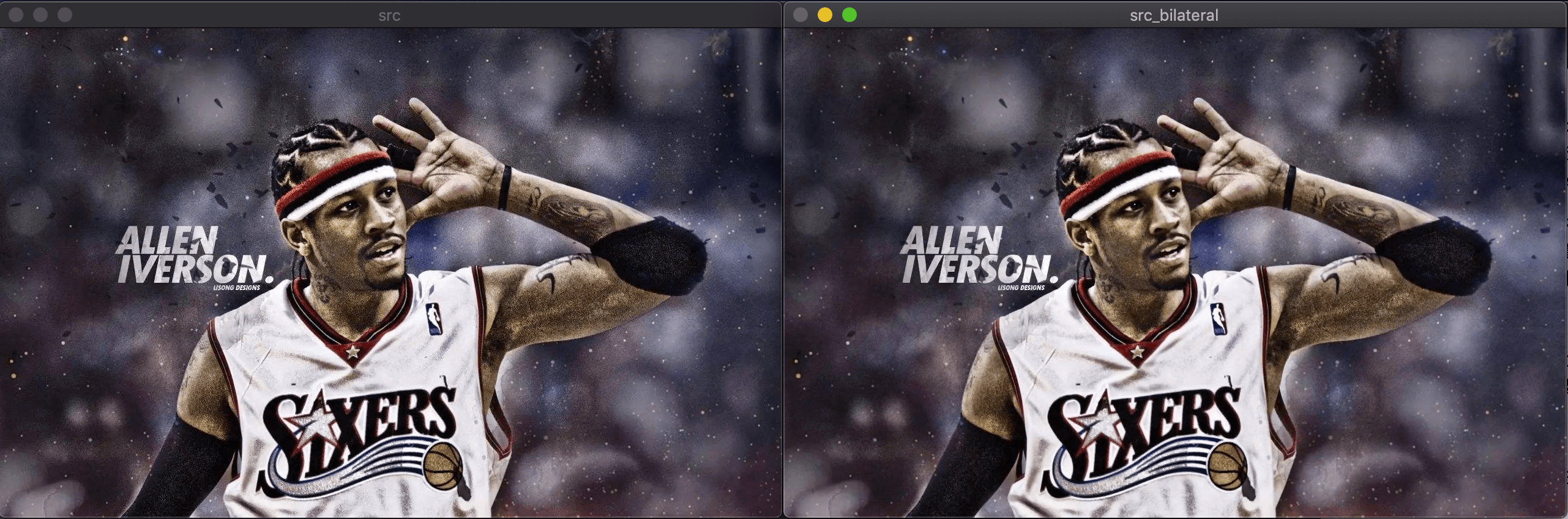
其效果见下(左侧为原图,右侧为双边模糊后的图):
1
bilateralFilter(src,src_bilateral,3,100,3);
6.高斯分布
高斯分布(Gaussian distribution)又名正态分布。
👉一维高斯分布的概率密度函数为:
\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma ^2}}\]👉高维高斯分布的概率密度函数为:
\[f(\bar x)=\frac{1}{(2\pi)^{D/2}} \frac{1}{\mid \sum \mid ^{1/2}} e^{ -\frac{1}{2} (\bar x-\bar \mu)^T \sum^{-1} (\bar x-\bar \mu) }\]其中,$\bar x$表示维度为D的向量,$\bar \mu$则是这些向量的平均值,$\sum$表示所有向量$\bar x$的协方差矩阵,$\mid \sum \mid$表示协方差矩阵的行列式。
因此根据高维高斯分布的公式,我们可以得到二维高斯分布的概率密度函数为:
\[f(\bar x)=\frac{1}{(2\pi)\mid \sum \mid ^{1/2}} e^{-\frac{1}{2}[(\frac{x_1-\mu_1}{\sigma_1})^2 + (\frac{x_2-\mu_2}{\sigma_2})^2]}\]二维高斯分布的图像为: