【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.前言
在【机器学习基础】第十一课:决策树的基本流程一文中,我们可以看出决策树学习的关键是如何选择最优划分属性。
一般而言,随着划分过程不断进行,我们希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度”(purity)越来越高。
2.信息增益
“信息熵”(information entropy)是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第k类样本所占的比例为$p_k,(k=1,2,…,\mid y \mid)$,则D的信息熵定义为:
\[Ent(D)=-\sum_{k=1}^{\mid y \mid} p_k\log_2 p_k \tag{2.1}\]注意区分信息熵和交叉熵。
$Ent(D)$的值越小,则D的纯度越高。其中,$\mid y \mid$表示样本类别总数。
⚠️计算信息熵时约定:若$p=0$,则$p\log_2 p=0$。
‼️$Ent(D)$的最小值为0,最大值为$log_2 \mid y \mid$。详细证明参见本文2.1部分。
假定离散属性a有V个可能的取值$\{a^1,a^2,…,a^V \}$,若使用a来对样本集D进行划分,则会产生V个分支结点,其中第v个分支结点包含了D中所有在属性a上取值为$a^v$的样本,记为$D^v$。
我们可以根据式(2.1)计算出$D^v$的信息熵,再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重$\frac{\mid D^v \mid}{\mid D \mid}$,即样本数越多的分支结点的影响越大,于是可计算出用属性a对样本集D进行划分所获得的“信息增益”(information gain):
\[Gain(D,a)=Ent(D)-\sum_{v=1}^V \frac{\mid D^v \mid}{\mid D \mid} Ent(D^v) \tag{2.2}\]一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的“纯度提升”越大。
因此,我们可用信息增益来进行决策树的划分属性选择。著名的ID3决策树学习算法就是以信息增益为准则来选择划分属性。
ID3名字中的ID是Iterative Dichotomiser(迭代二分器)的简称。
2.1.信息熵取值范围的证明
在第2部分的信息熵公式中,若令$\mid y \mid=n,p_k=x_k$,那么信息熵$Ent(D)$就可以看作一个n元实值函数,即:
\[Ent(D)=f(x_1,x_2,...,x_n)=-\sum_{k=1}^n x_k \log_2 x_k\]其中,$0\leq x_k \leq 1,\sum_{k=1}^n x_k=1$。
2.1.1.信息熵取值范围的最大值
如果不考虑约束$0\leq x_k \leq 1$,仅考虑$\sum_{k=1}^n x_k=1$的话,对$f(x_1,x_2,…,x_n)$求最大值等价于如下最小化问题:
\[\begin{align*} &\min \quad \sum_{k=1}^n x_k \log_2 x_k \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& \sum_{k=1}^n x_k=1 \\ \end{array} \end{align*}\]根据拉格朗日乘子法可知,该优化问题的拉格朗日函数为:
\[L(x_1,x_2,...,x_n,\lambda)=\sum_{k=1}^n x_k \log_2 x_k+\lambda(\sum_{k=1}^n x_k -1)\]其中,$\lambda$为拉格朗日乘子。对$L(x_1,x_2,…,x_n,\lambda)$分别关于$x_1,x_2,…,x_n,\lambda$求一阶偏导数,并令偏导数等于0可得:
\[\begin{align} \frac{\partial L(x_1,x_2,...,x_n,\lambda)}{\partial x_1} &= \frac{\partial}{\partial x_1} [\sum_{k=1}^n x_k \log_2 x_k+\lambda (\sum_{k=1}^n x_k -1)] \\ &= \log_2 x_1 + x_1 \cdot \frac{1}{x_1} \cdot \log_2 e + \lambda \\&= \log_2 x_1 + \frac{1}{\ln 2} + \lambda \\&= 0 \end{align}\]$\log_a b \cdot \log_b a=1$
求得:$\lambda=-\log_2 x_1-\frac{1}{\ln 2}$。同理:
- $\frac{\partial L(x_1,x_2,…,x_n,\lambda)}{\partial x_2}=0$推出:$\lambda=-\log_2 x_2-\frac{1}{\ln 2}$
- ……
- $\frac{\partial L(x_1,x_2,…,x_n,\lambda)}{\partial x_n}=0$推出:$\lambda=-\log_2 x_n-\frac{1}{\ln 2}$
此外:
\[\begin{align} \frac{\partial L(x_1,x_2,...,x_n,\lambda)}{\partial \lambda} &= \frac{\partial}{\partial \lambda} [\sum_{k=1}^n x_k \log_2 x_k+\lambda (\sum_{k=1}^n x_k -1)] \\ &= 0 \end{align}\]可推出:$\sum_{k=1}^n x_k=1$。
整理上述式子可得:
\[\left\{ \begin{array}{} \lambda=-\log_2 x_1-\frac{1}{\ln 2}=-\log_2 x_2-\frac{1}{\ln 2}=\cdots = -\log_2 x_n-\frac{1}{\ln 2} \\ \sum_{k=1}^n x_k=1 \end{array} \right.\]由以上方程组可解得:
\[x_1=x_2=\cdots =x_n=\frac{1}{n}\]又因为$x_k$还需满足约束$0\leq x_k \leq 1$,此处显然有$0\leq \frac{1}{n} \leq 1$,所以$x_1=x_2=\cdots =x_n=\frac{1}{n}$是满足所有约束的最优解,也即为当前最小化问题的最小值点,同时也是$f(x_1,x_2,…,x_n)$的最大值点。将$x_1=x_2=\cdots =x_n=\frac{1}{n}$代入$f(x_1,x_2,…,x_n)$中可得:
\[f(\frac{1}{n},...,\frac{1}{n})=-\sum_{k=1}^n \frac{1}{n} \log_2 \frac{1}{n}=-n\cdot \frac{1}{n} \log_2 \frac{1}{n}=\log_2 n\]$\log_a M^n=n\log_a M$
所以$f(x_1,x_2,…,x_n)$在满足约束$0\leq x_k \leq 1,\sum_{k=1}^n x_k=1$时的最大值为$\log_2 n$。
2.1.2.信息熵取值范围的最小值
如果不考虑约束$\sum_{k=1}^n x_k=1$,仅考虑$0\leq x_k \leq 1$的话,$f(x_1,…,x_n)$可以看做是n个互不相关的一元函数的加和,也即:
\[f(x_1,...,x_n)=\sum_{k=1}^n g(x_k)\]其中,$g(x_k)=-x_k \log_2 x_k,0\leq x_k \leq 1$。那么当$g(x_1),g(x_2),…,g(x_n)$分别取到其最小值时,$f(x_1,…,x_n)$也就取到了最小值。所以接下来考虑分别求$g(x_1),g(x_2),…,g(x_n)$各自的最小值。由于$g(x_1),g(x_2),…,g(x_n)$的定义域和函数表达式均相同,所以只需求出$g(x_1)$的最小值也就求出了$g(x_2),…,g(x_n)$的最小值。
下面考虑求$g(x_1)$的最小值,首先对$g(x_1)$关于$x_1$求一阶和二阶导数:
\[g'(x_1)=-\log_2 x_1 - \frac{1}{\ln 2}\] \[g''(x_1)=-\frac{1}{x_1 \ln2}\]显然,当$0\leq x_k \leq 1$时,$g”(x_1)=-\frac{1}{x_1 \ln2}$恒小于0,所以$g(x_1)$是一个在其定义域范围内开口向下的凹函数,那么其最小值必然在边界取,于是分别取$x_1=0$和$x_1=1$,代入$g(x_1)$可得:
\[g(0)=-0\log_2 0=0\] \[g(1)=-1\log_2 1=0\]所以,$g(x_1)$的最小值为0,同理可得$g(x_2),…,g(x_n)$的最小值也为0,那么$f(x_1,…,x_n)$的最小值此时也为0。但是,此时是不考虑约束$\sum_{k=1}^n x_k=1$,仅考虑$0\leq x_k \leq 1$时取到的最小值。若考虑约束$\sum_{k=1}^n x_k=1$的话,那么$f(x_1,…,x_n)$的最小值一定大于等于0。
如果令某个$x_k=1$,那么根据约束$\sum_{k=1}^n x_k=1$可知$x_1=x_2=…=x_{k-1}=x_{k+1}=…=x_n=0$,将其代入$f(x_1,…,x_n)$可得:
\[f(0,0,...,0,1,0,...,0)=0\]所以,$x_k=1,x_1=x_2=…=x_{k-1}=x_{k+1}=…=x_n=0$一定是$f(x_1,…,x_n)$在满足约束$\sum_{k=1}^n x_k=1$和$0\leq x_k \leq 1$下的最小值,其最小值为0。
2.2.信息增益应用举例
假设我们有如下西瓜训练集:
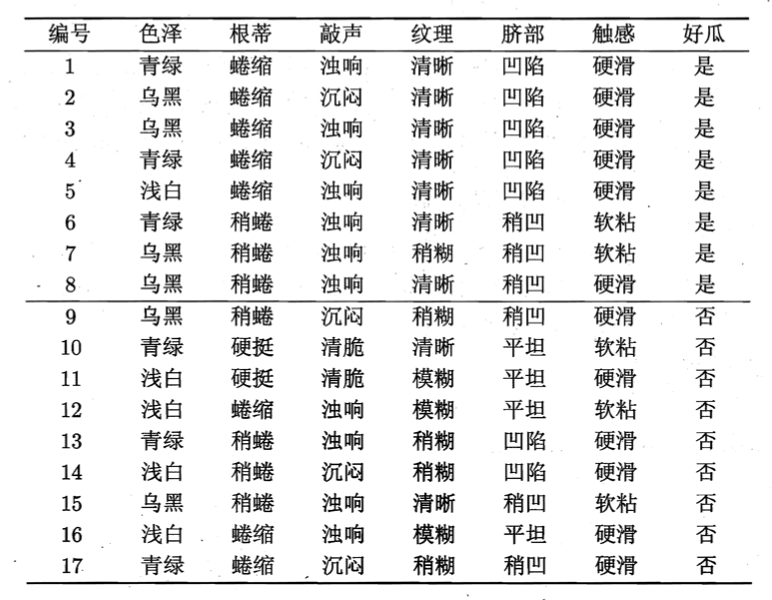
显然,$\mid y \mid=2$。
计算根结点的信息熵为:
\[Ent(D)=-\sum_{k=1}^2 p_k \log_2 p_k=-(\frac{8}{17} \log_2 \frac{8}{17}+\frac{9}{17} \log_2 \frac{9}{17})=0.998\]然后,我们要计算出当前属性集合{色泽,根蒂,敲声,纹理,脐部,触感}中每个属性的信息增益。
以属性“色泽”为例,它有3个可能的取值:{青绿,乌黑,浅白}。若使用该属性对D进行划分,则可得到3个子集,分别记为:$D^1$(色泽=青绿),$D^2$(色泽=乌黑),$D^3$(色泽=浅白)。计算出用“色泽”划分之后所获得的3个分支结点的信息熵为:
- $Ent(D^1)=-(\frac{3}{6} \log_2 \frac{3}{6}+\frac{3}{6} \log_2 \frac{3}{6})=1.000$
- $Ent(D^2)=-(\frac{4}{6} \log_2 \frac{4}{6}+\frac{2}{6} \log_2 \frac{2}{6})=0.918$
- $Ent(D^3)=-(\frac{1}{5} \log_2 \frac{1}{5}+\frac{4}{5} \log_2 \frac{4}{5})=0.722$
于是,根据式(2.2)可计算出属性“色泽”的信息增益为:
\[Gain(D,色泽)=0.998-(\frac{6}{17}\times 1.000 + \frac{6}{17}\times 0.918 + \frac{5}{17} \times 0.722)=0.109\]类似的,我们可计算出其他属性的信息增益:
- $Gain(D,根蒂)=0.143$
- $Gain(D,敲声)=0.141$
- $Gain(D,纹理)=0.381$
- $Gain(D,脐部)=0.289$
- $Gain(D,触感)=0.006$
显然,属性“纹理”的信息增益最大,于是它被选为划分属性:
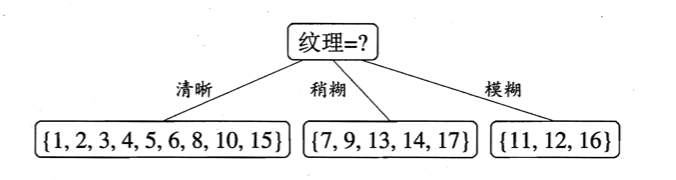
然后,决策树学习算法将对每个分支结点做进一步划分,以第一个分支结点(“纹理=清晰”)为例,该结点可用的属性集合为{色泽,根蒂,敲声,脐部,触感}。基于$D^1$计算出各属性的信息增益。
“纹理”不再作为候选划分属性。
依旧以属性“色泽”为例,首先计算其各个子属性的信息熵:
- $Ent(D^1)=-(\frac{3}{4} \log_2 \frac{3}{4} + \frac{1}{4} \log_2 \frac{1}{4})=0.811$
- $Ent(D^2)=-(\frac{3}{4} \log_2 \frac{3}{4} + \frac{1}{4} \log_2 \frac{1}{4})=0.811$
- $Ent(D^3)=0$
父结点(“纹理=清晰”)的信息熵为:
\[Ent(“纹理=清晰”)=-(\frac{7}{9} \log_2 \frac{7}{9} + \frac{2}{9} \log_2 \frac{2}{9} )=0.764\]求得属性“色泽”的信息增益为:
\[Gain(D^1,色泽)=0.764-(\frac{4}{9} \times 0.811+\frac{4}{9} \times 0.811 +\frac{1}{9} \times 0)=0.043\]同理:
- $Gain(D^1,根蒂)=0.458$
- $Gain(D^1,敲声)=0.331$
- $Gain(D^1,脐部)=0.458$
- $Gain(D^1,触感)=0.458$
“根蒂”、“脐部”、“触感”3个属性均取得了最大的信息增益,可任选其中之一作为划分属性。类似的,对每个分支结点进行上述操作,最终可得到如下决策树:
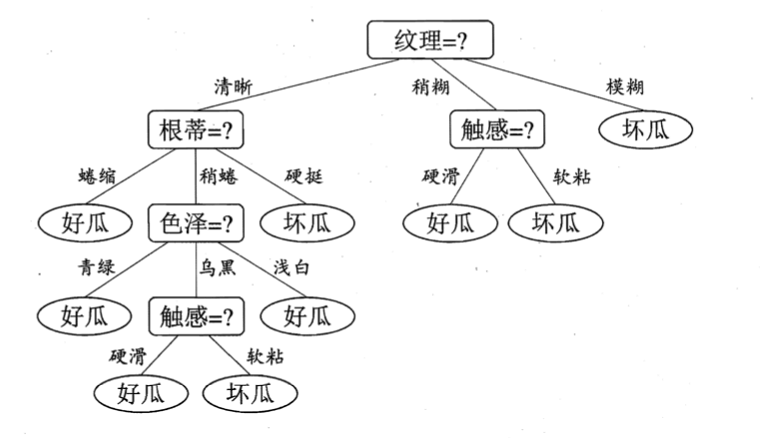
3.增益率
在第2部分,我们有意忽略了数据集中的“编号”这一列。若把“编号”也作为一个候选划分属性,可计算出其信息增益为0.998,远大于其他候选划分属性。这很容易理解:“编号”将产生17个分支,每个分支结点仅包含一个样本,这些分支结点的纯度已达最大。然而,这样的决策树显然不具有泛化能力,无法对新样本进行有效预测。
实际上,信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著名的C4.5决策树算法不直接使用信息增益,而是使用“增益率”(gain ratio)来选择最优划分属性。增益率定义为:
\[Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)} \tag{3.1}\]其中,
\[IV(a)=-\sum_{v=1}^V \frac{\mid D^v \mid}{\mid D \mid} \log_2 \frac{\mid D^v \mid}{\mid D \mid}\]称为属性a的“固有值”。属性a的可能取值数目越多(即V越大),则$IV(a)$的值通常会越大。
⚠️需注意的是,增益率准则对可取值数目较少的属性有所偏好。因此,C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
4.基尼指数
CART决策树使用“基尼系数”(Gini index)来选择划分属性。
CART是“Classification and Regression Tree”的简称,可用于分类和回归任务。
数据集D的纯度可用基尼值来度量:
\[Gini(D)=\sum_{k=1}^{\mid y \mid} \sum_{k'\neq k}p_k p_{k'}=\sum_{k=1}^{\mid y \mid} p_k (1-p_k)=1-\sum_{k=1}^{\mid y \mid} p_k^2\]直观来说,$Gini(D)$反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率。因此,$Gini(D)$越小,则数据集D的纯度越高。
属性a的基尼指数定义为:
\[Gini\_index(D,a)=\sum_{v=1}^V \frac{\mid D^v \mid}{\mid D \mid} Gini(D^v)\]于是,我们在候选属性集合A中,选择那个使得划分后基尼指数最小的属性作为最优划分属性。