Deep Learning Series

【深度学习基础】第二十九课：经典的神经网络结构

LeNet-5，AlexNet，VGG-16

Posted by x-jeff on July 18, 2020

【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章，未经本人允许，禁止转载。转载请注明出处。

1.LeNet-5

相关链接：原文，博客讲解。

假设使用LeNet-5进行手写数字识别：

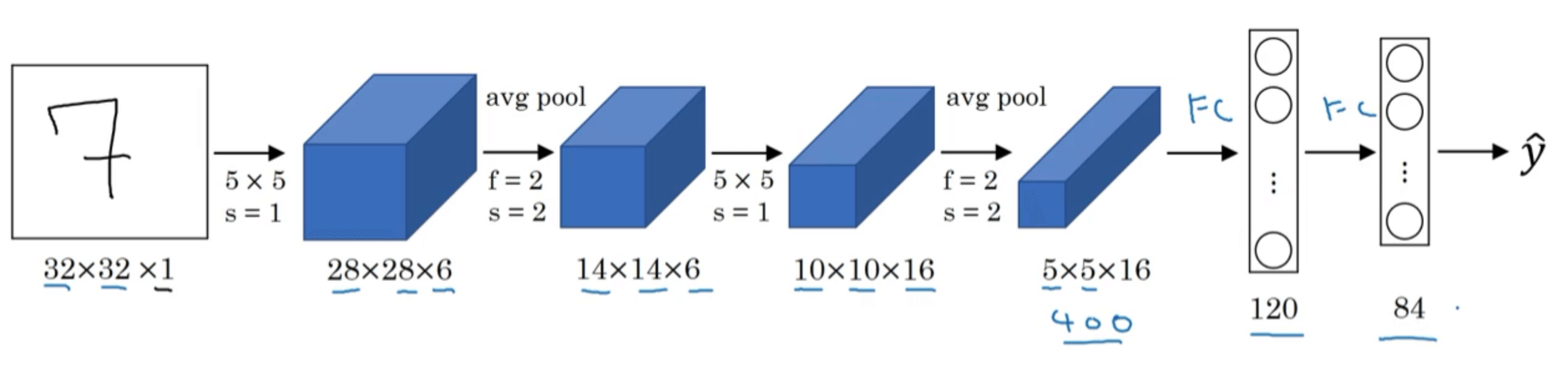
Layer Num Layer Type Input Filter Stride Padding Output
Layer0 Input Layer $\times$ $\times$ $\times$ $\times$ $32\times 32 \times 1$
Layer1 CONV1 $32\times 32 \times 1$ $5\times 5 \times 6$ 1 VALID $28\times 28\times 6$
  POOL1(AVG) $28\times 28\times 6$ $2\times 2$ 2 $\times$ $14\times 14 \times 6$
Layer2 CONV2 $14\times 14 \times 6$ $5\times 5 \times 16$ 1 VALID $10\times 10\times 16$
  POOL2(AVG) $10\times 10\times 16$ $2\times 2$ 2 $\times$ $5\times 5 \times 16$
Layer3 FC3 400 $\times$ $\times$ $\times$ 120
Layer4 FC4 120 $\times$ $\times$ $\times$ 84
Layer5 Output Layer 84 $\times$ $\times$ $\times$ 10

需要注意的地方：

  1. 在LeNet-5被创作的那个年代，人们更喜欢用average pooling。但是现在人们用max pooling更多一些。
  2. 在LeNet-5被创作的那个年代，人们并不使用padding。
  3. 输出层可以用softmax函数。而在原论文中，LeNet-5在输出层使用了另外一种现在已经很少用到的分类器，这里不再详述，有兴趣的可以去阅读原论文。
  4. LeNet-5网络的特点：
    • 随着层数的加深，图像的高度和宽度都在缩小，通道的数量一直在增加。
    • 一个或多个卷积层后面跟着一个池化层，然后又是若干个卷积层，再接一个池化层，然后是全连接层，最后是输出层。这种排列模式至今仍然经常被使用在很多神经网络结构中。
  5. 在原始论文中，作者使用的是sigmoid函数和tanh函数作为激活函数，并不是我们现在常用的ReLU函数。
  6. 在原始论文中，作者在池化层后进行了非线性函数（sigmoid函数）处理。
  7. LeNet-5中，5代表网络的层数。

2.AlexNet

相关链接：原文，博客讲解。

AlexNet网络是以论文的第一作者Alex Krizhevsky的名字命名的。其网络结构见下：

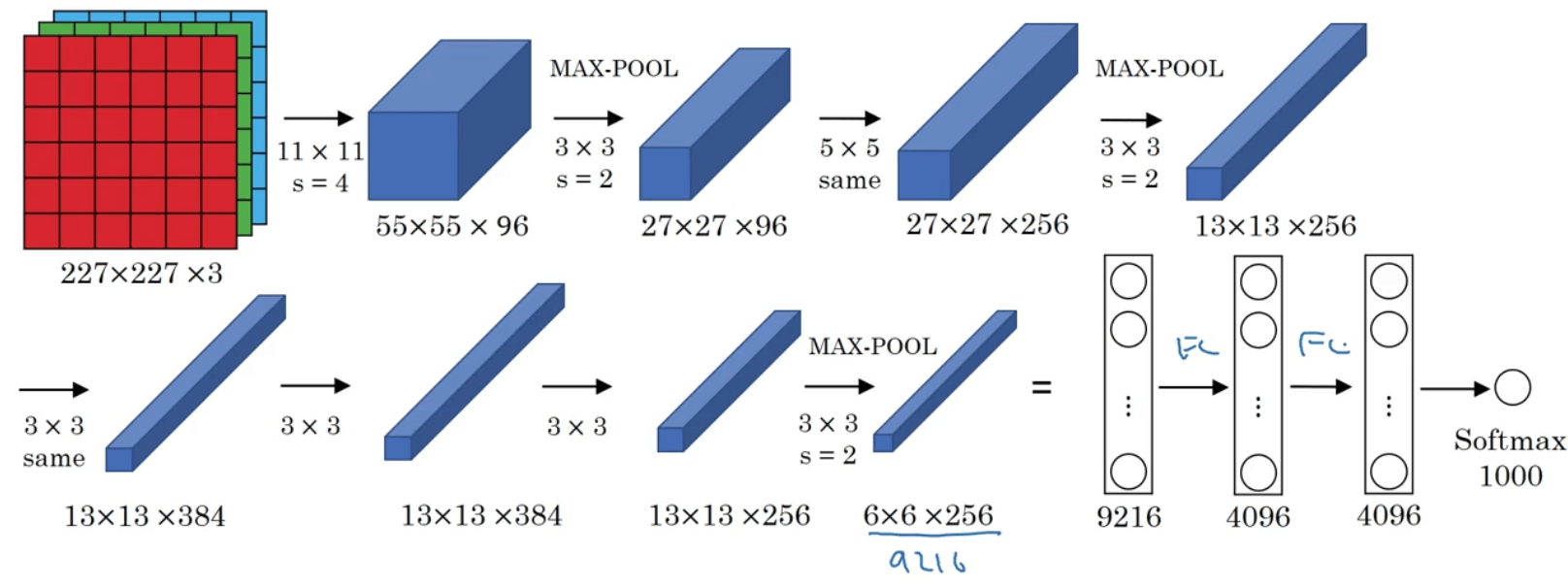
Layer Num Layer Type Input Filter Stride Padding Output
Layer0 Input Layer $\times$ $\times$ $\times$ $\times$ $227 \times 227 \times 3$
Layer1 CONV1 $227 \times 227 \times 3$ $11 \times 11 \times 96$ 4 VALID $55\times 55 \times 96$
  POOL1(MAX) $55\times 55 \times 96$ $3\times 3$ 2 $\times$ $27 \times 27 \times 96$
Layer2 CONV2 $27 \times 27 \times 96$ $5 \times 5 \times 256$ 1 SAME $27 \times 27 \times 256$
  POOL2(MAX) $27 \times 27 \times 256$ $3\times 3$ 2 $\times$ $13\times 13 \times 256$
Layer3 CONV3 $13\times 13 \times 256$ $3\times 3 \times 384$ 1 SAME $13\times 13 \times 384$
Layer4 CONV4 $13\times 13 \times 384$ $3\times 3 \times 384$ 1 SAME $13\times 13 \times 384$
Layer5 CONV5 $13\times 13 \times 384$ $3\times 3 \times 256$ 1 SAME $13\times 13 \times 256$
  POOL5(MAX) $13\times 13 \times 256$ $3\times 3$ 2 $\times$ $6\times 6 \times 256$
Layer6 FC6 9216 $\times$ $\times$ $\times$ 4096
Layer7 FC7 4096 $\times$ $\times$ $\times$ 4096
Layer8 Output Layer 4096 $\times$ $\times$ $\times$ 1000

需要注意的地方：

  1. 实际上原文中使用的图像是$224 \times 224 \times 3$。
  2. 上述例子假设输出层有1000个神经元。
  3. 所用的激活函数为ReLU函数。
  4. 原始论文中，AlexNet还使用了另一种类型的层，叫做“局部响应归一化层（local response normalization,LRN）”。LRN的基本思路是将某一位置所有通道的数值进行归一化，如下图所示：
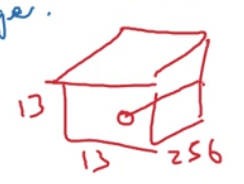
  5. 现在的很多研究者发现LRN起不到太大作用，因此逐渐被弃用。

3.VGG-16

相关链接：原文，博客讲解。

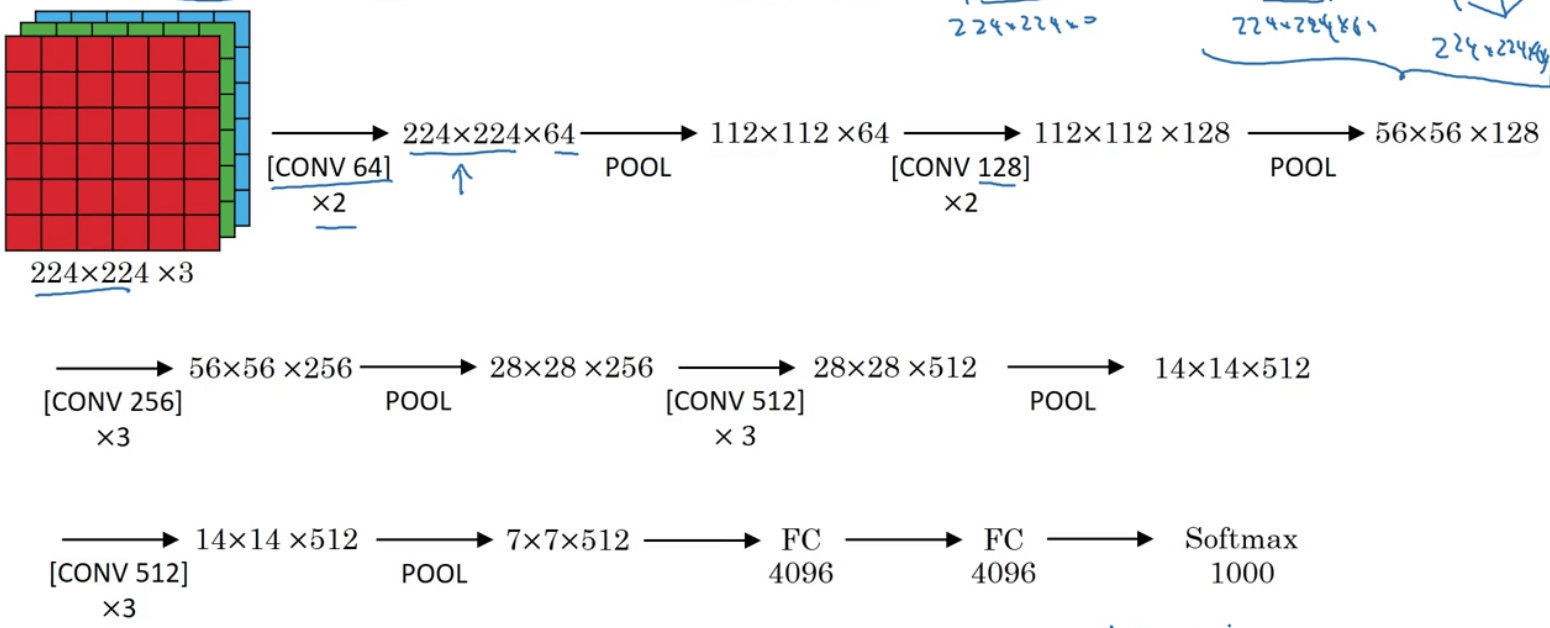
Layer Num Layer Type Input Filter Stride Padding Output
Layer0 Input Layer $\times$ $\times$ $\times$ $\times$ $224 \times 224 \times 3$
Layer1 CONV1 $224 \times 224 \times 3$ $3\times 3 \times 64$ 1 SAME $224\times 224 \times 64$
Layer2 CONV2 $224 \times 224 \times 64$ $3\times 3 \times 64$ 1 SAME $224\times 224 \times 64$
  POOL2(MAX) $224\times 224 \times 64$ $2\times 2$ 2 $\times$ $112\times 112\times 64$
Layer3 CONV3 $112\times 112\times 64$ $3\times 3\times 128$ 1 SAME $112\times 112 \times 128$
Layer4 CONV4 $112\times 112\times 128$ $3\times 3\times 128$ 1 SAME $112\times 112 \times 128$
  POOL4(MAX) $112\times 112 \times 128$ $2\times 2$ 2 $\times$ $56 \times 56 \times 128$
Layer5 CONV5 $56 \times 56 \times 128$ $3\times 3\times 256$ 1 SAME $56\times 56 \times 256$
Layer6 CONV6 $56 \times 56 \times 256$ $3\times 3\times 256$ 1 SAME $56\times 56 \times 256$
Layer7 CONV7 $56 \times 56 \times 256$ $3\times 3\times 256$ 1 SAME $56\times 56 \times 256$
  POOL7(MAX) $56\times 56 \times 256$ $2\times 2$ 2 $\times$ $28\times 28 \times 256$
Layer8 CONV8 $28\times 28 \times 256$ $3\times 3\times 512$ 1 SAME $28\times 28 \times 512$
Layer9 CONV9 $28\times 28 \times 512$ $3\times 3\times 512$ 1 SAME $28\times 28 \times 512$
Layer10 CONV10 $28\times 28 \times 512$ $3\times 3\times 512$ 1 SAME $28\times 28 \times 512$
  POOL10(MAX) $28\times 28 \times 512$ $2\times 2$ 2 $\times$ $14\times 14 \times 512$
Layer11 CONV11 $14\times 14 \times 512$ $3\times 3\times 512$ 1 SAME $14\times 14 \times 512$
Layer12 CONV12 $14\times 14 \times 512$ $3\times 3\times 512$ 1 SAME $14\times 14 \times 512$
Layer13 CONV13 $14\times 14 \times 512$ $3\times 3\times 512$ 1 SAME $14\times 14 \times 512$
  POOL13(MAX) $14\times 14 \times 512$ $2\times 2$ 2 $\times$ $7\times 7 \times 512$
Layer14 FC14 25088 $\times$ $\times$ $\times$ 4096
Layer15 FC15 4096 $\times$ $\times$ $\times$ 4096
Layer16 Output Layer 4096 $\times$ $\times$ $\times$ 1000

需要注意的地方：

  1. 上述例子中假设输出层有1000个神经元。
  2. VGG-16中的16代表着网络的层数。
  3. 类似的衍生网络，如VGG-19。
CATALOG
    FEATURED TAGS
    README Machine Learning Series Mathematics Series Image Segmentation Python Series Fundamentals of Computers OpenCV Series C++ Series Deep Learning Series Conda Tensorflow Series Algorithms Series AI Papers Object Recognition Natural Language Processing Aha! Algorithms Camera Calibration How Program Works Optical Flow Estimation How Networks Work Computer Vision Source Code CUDA C++ Programming Guide C++ Concurrency IN ACTION