【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.前言
在深度学习中,随着网络层数的增多一般会伴随着下面几个问题:
- 计算资源的消耗。
- 模型容易过拟合。
- 梯度消失/梯度爆炸问题的产生。
问题1通过提升硬件即可解决;问题2可以采用正则化方法,例如添加正则项、使用dropout等;问题3可以通过BatchNorm避免。
既然这些问题都可以解决,并且从理论上来说,网络越深,效果应该越好,那么我们一味的加深网络深度是否就可以获得更好的效果呢?答案是否定的。随着网络层数的增加,网络发生了退化(degradation)的现象:随着网络层数的增多,训练集loss逐渐下降,然后趋于饱和,当再增加网络深度的话,优化算法很难训练,训练错误会越来越多,训练集loss反而会增大。
当网络退化时,浅层网络能够达到比深层网络更好的训练效果,这时如果我们把低层的特征传到高层,那么效果应该至少不比浅层的网络效果差。而残差网络(Residual Networks,ResNets)的主要思想就是将浅层特征直接映射到深层,从而解决了更深层次神经网络的训练问题,也使网络准确率得到显著提升。
2.残差网络的结构
首先介绍下什么是残差块。假设下图是神经网络中的两层:
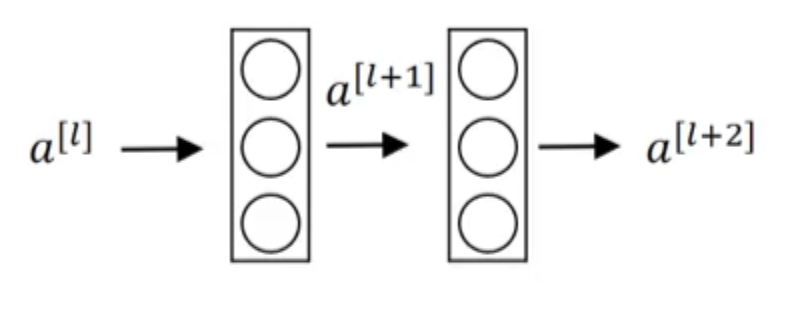
前向传播的计算过程为($g(\cdot)$表示激活函数,一般为ReLU函数):
- $z^{[l+1]}=W^{[l+1]}a^{[l]}+b^{[l+1]}$
- $a^{[l+1]}=g(z^{[l+1]})$
- $z^{[l+2]}=W^{[l+2]}a^{[l+1]}+b^{[l+2]}$
- $a^{[l+2]}=g(z^{[l+2]})$
这条传播路径称为“main path”,在残差网络中,我们额外增加一条路径,称为“short cut”或“skip connection”:

将前向传播的计算过程改为:
- $z^{[l+1]}=W^{[l+1]}a^{[l]}+b^{[l+1]}$
- $a^{[l+1]}=g(z^{[l+1]})$
- $z^{[l+2]}=W^{[l+2]}a^{[l+1]}+b^{[l+2]}$
- $a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$
在第4行公式中额外加上的$a^{[l]}$便产生了一个残差块。
构建一个ResNets就是通过很多这样的残差块堆积在一起,形成一个深度神经网络。
接下来我们一起来看下如何将一个“plain network”(如下图所示,即普通的神经网络)改造成ResNets:

添加所有的“skip connection”,得到ResNets:
