本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.主成分分析的作用
主成分分析(Principal Component Analysis,简称PCA)是在机器学习以及统计学领域内常用的一种线性降维方法。其可以有效地降低数据维度,比如说:将原本高维的数据(N维)重新以一个相对低维的形式表达(K维,且$K<N$)。理想上只要该K维的表征(representation)具有代表性,能够抓住原来N维数据的大部分特性,并且没有损失过多信息,我们便可以用K维来代表之前的N维。
2.PCA的直观理解
假设我们有20组样本,每个样本有两个特征$f_1,f_2$:
\[\begin{bmatrix} 2.89 & 1.52 \\ 0.32 & 0.91 \\ 5.8 & 1.52 \\ -6.52 & -0.88 \\ 3.94 & -0.03 \\ -4.21 & -1.26 \\ 0.45 & -0.25 \\ 2.14 & 0.96 \\ 1.3 & -0.89 \\ -4.98 & -0.45 \\ -2.4 & -0.88 \\ -3.1 & -1.12 \\ 0.69 & -0.86 \\ -1.59 & 0.13 \\ -3.64 & -1.53 \\ -0.24 & 0.51 \\ 6.81 & 2.66 \\ 4.63 & 1.28 \\ -2.24 & -0.14 \\ -0.06 & -1.19 \\ \end{bmatrix}\]如果现在我们只想用一个特征来描述这些样本,那么我们该怎么办呢?
最容易想到的办法就是将这些点画在笛卡尔坐标系(即直角坐标系)下,然后观察这些点是否会存在某种关系。将数据的第一特征$f_1$和第二特征$f_2$分别作为$x,y$坐标绘制在坐标系中:
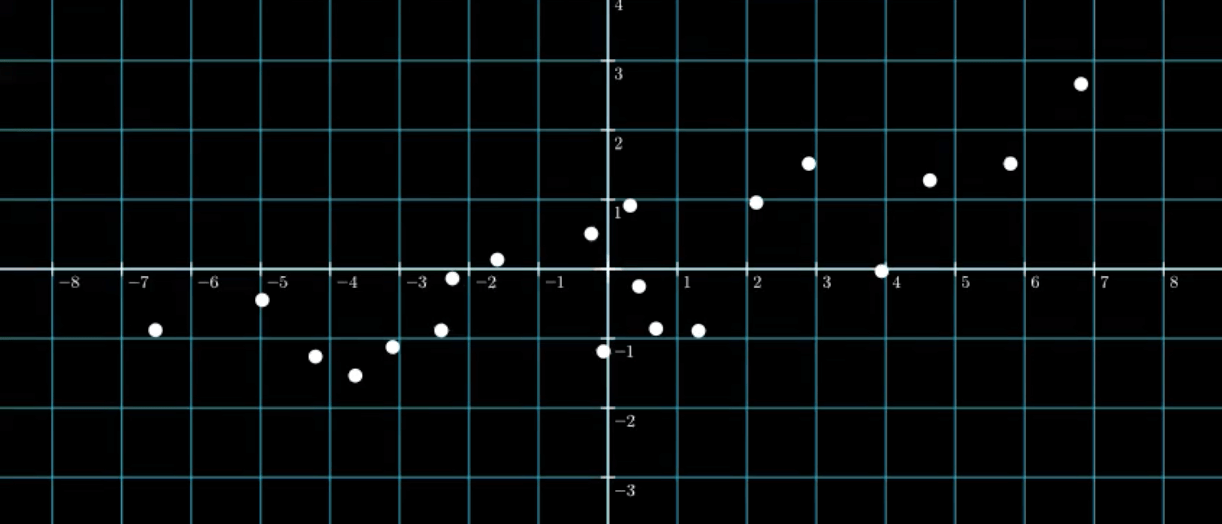
我们这里所用的两个基底向量为:
\[\begin{align} \vec{i} = \begin{bmatrix} 1\\0 \end{bmatrix}, \vec{j} = \begin{bmatrix} 0\\1 \end{bmatrix} \end{align}\]所谓的坐标其实就是基底向量的线性组合:
\[\begin{bmatrix} x\\y \end{bmatrix}=f_1 \vec{i} + f_2 \vec{j}\]我们常把基底向量$\{\vec{i},\vec{j} \}$称作标准基底$B_{standard}$,而$(x,y)$坐标则是该基底的成分表征(Component Representation)。此外,可以把$\{\vec{i},\vec{j} \}$当成是二维向量空间里面的基础成分(Component)。
其实主成分分析的终极目标就是:找出一组最能代表我们手中数据的主成分,并以此为基底重新得到数据的成分表征。这个新的成分表征能为数据降维、去关联并帮助我们理解数据本质。
很明显,这些点存在着某种程度的线性关系:

将每个点都投影到拟合的直线上:
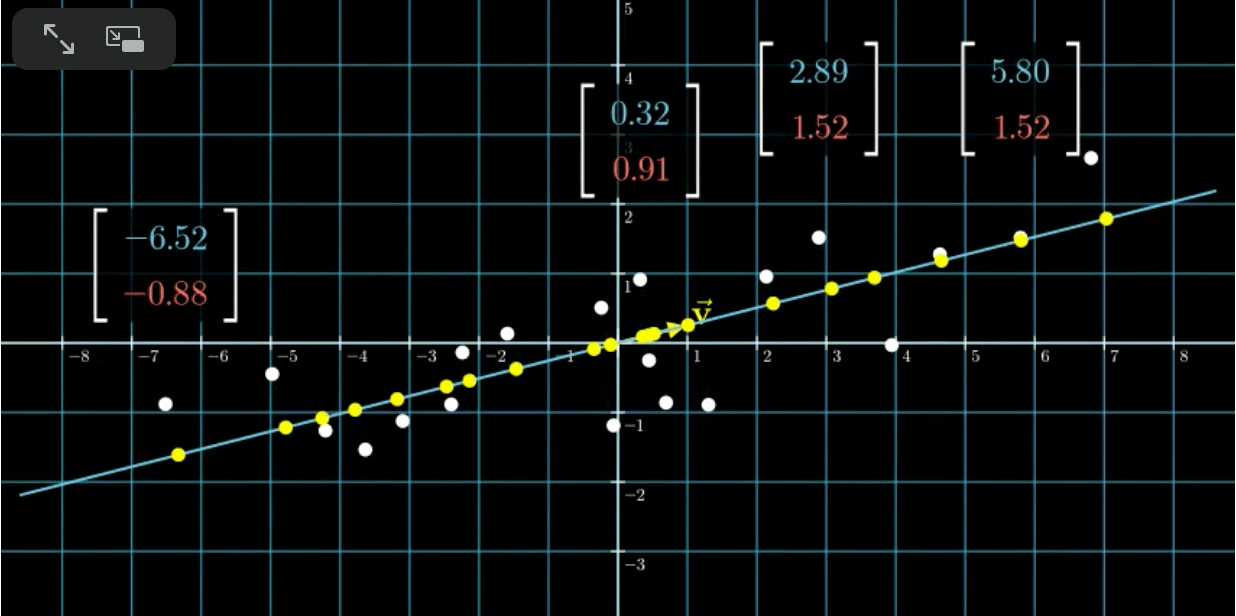
在有单位向量$\vec{v}$的情况下,每个黄色点都对应一个值,这些值便是我们将维度降到1之后得到的结果。这个新的基$\vec v$便是我们所要找的“主成分”。这便是一个非常简单的PCA的例子。
3.PCA原理剖析
在前两部分中,我们都提到过PCA的核心思想是通过低维特征来代表高维特征。那么我们该如何确定得到的低维特征是否可以很好的代表原有的高维特征呢?或者说,在第2部分的例子中,我们该如何确定拟合直线的位置呢?
一般来说,当某降维结果具有以下两个特性时,我们会认为是理想的:
- 最大变异:降维后所得到的新K维特征L具有最大的变异(Variance)。
- 最小错误:用K维的新特征L重新构建回N维数据能得到最小的重建错误(Reconstruction Error)。
其实这两个特性是等价的,当满足其中一个时,另一个自然而然的也会被满足。
先来说说“最小错误”,这里的“错误”其实就是降维前的数据到降维后的数据之间的距离:
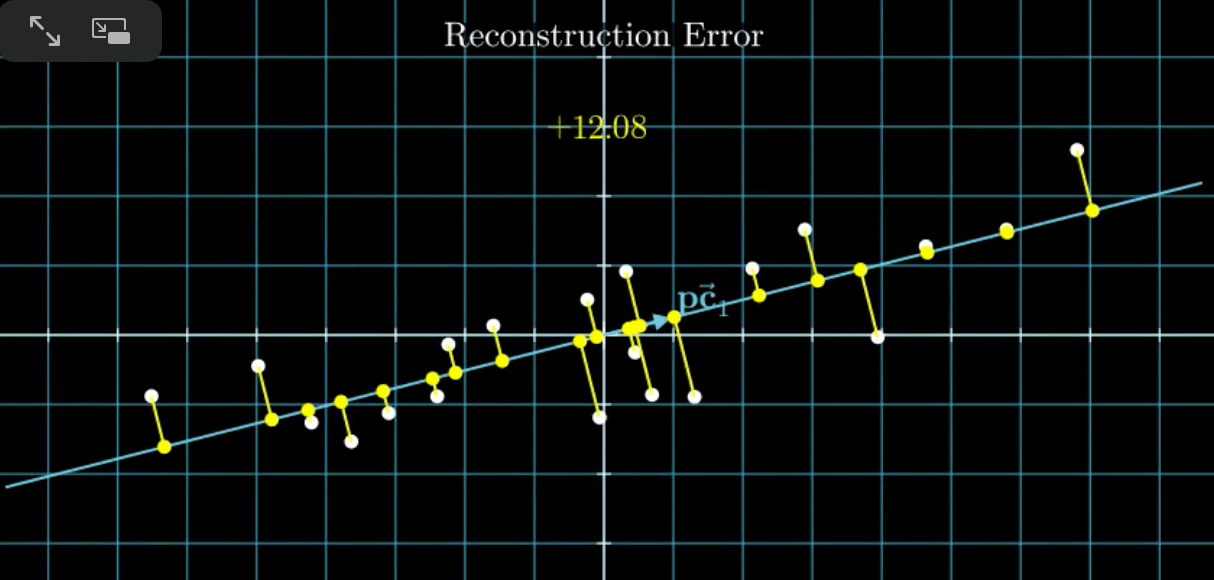
“最小错误”就是找到这样一条拟合直线,使得距离之和(即黄线的长度之和)最小,可以通过最小二乘法来确定。并且,这条拟合直线同时也满足“最大变异”。
接下来我们以“最大变异”为例,详细介绍下PCA的算法流程。
4.PCA的算法流程
算法输入:n维样本集$X_{n\times m}=(x_1,x_2,…,x_m)$,要降维到的目标维数$k$。
算法输出:降维后的样本集$Y$。
算法流程:
- 对所有样本进行中心化:$x_i=x_i-\frac{1}{m}\sum_{j=1}^m x_j$。
- 计算样本的协方差矩阵。
- 求出协方差矩阵的特征值及对应的特征向量。
- 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵$P_{k\times n}$。
- $Y_{k\times m}=P_{k\times n}X_{n\times m}$即为降维到k维后的数据。