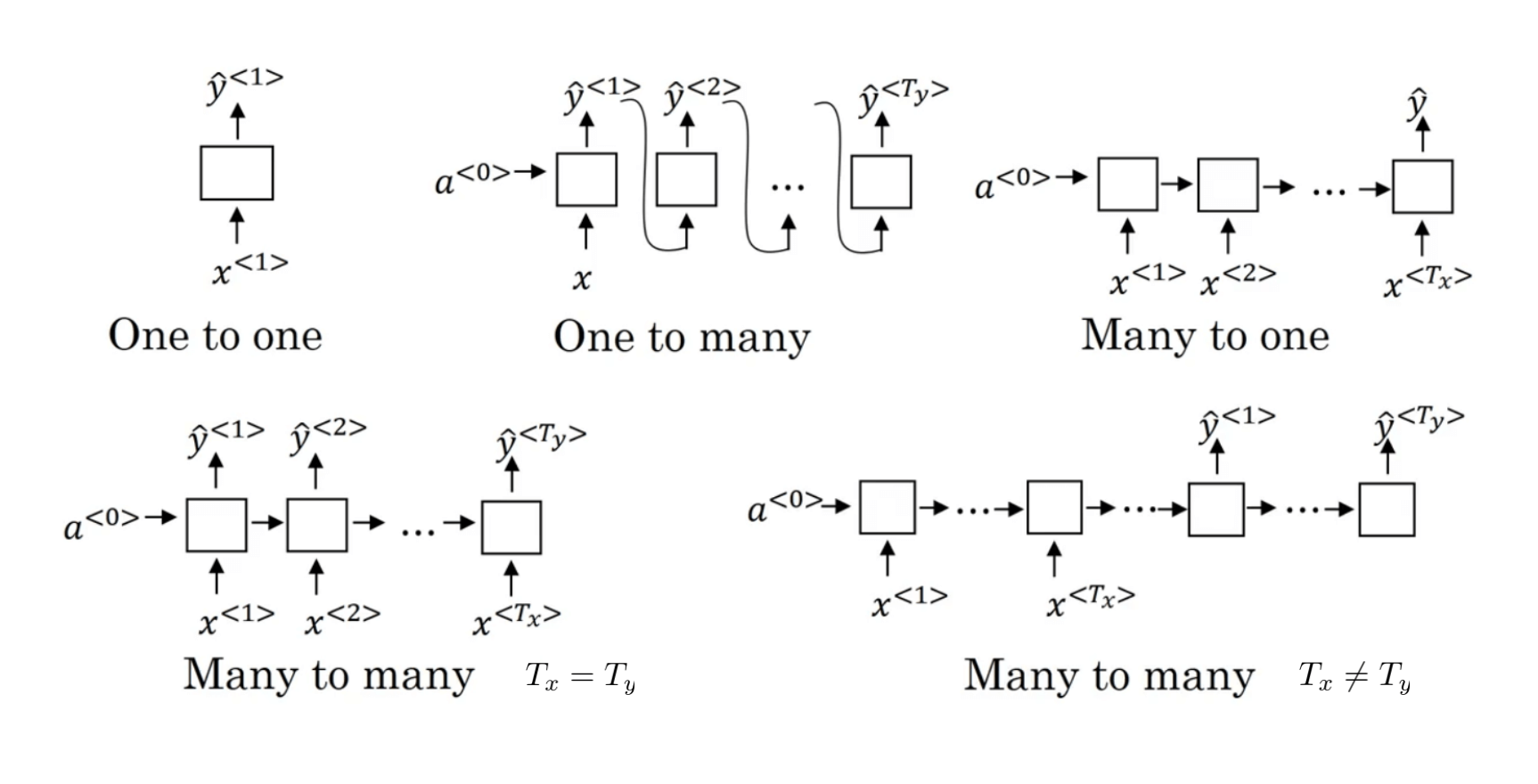【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.循环神经网络
依旧使用【深度学习基础】第三十九课:序列模型中第2部分的例子。假设我们用一个标准的神经网络结构来解决这个问题:
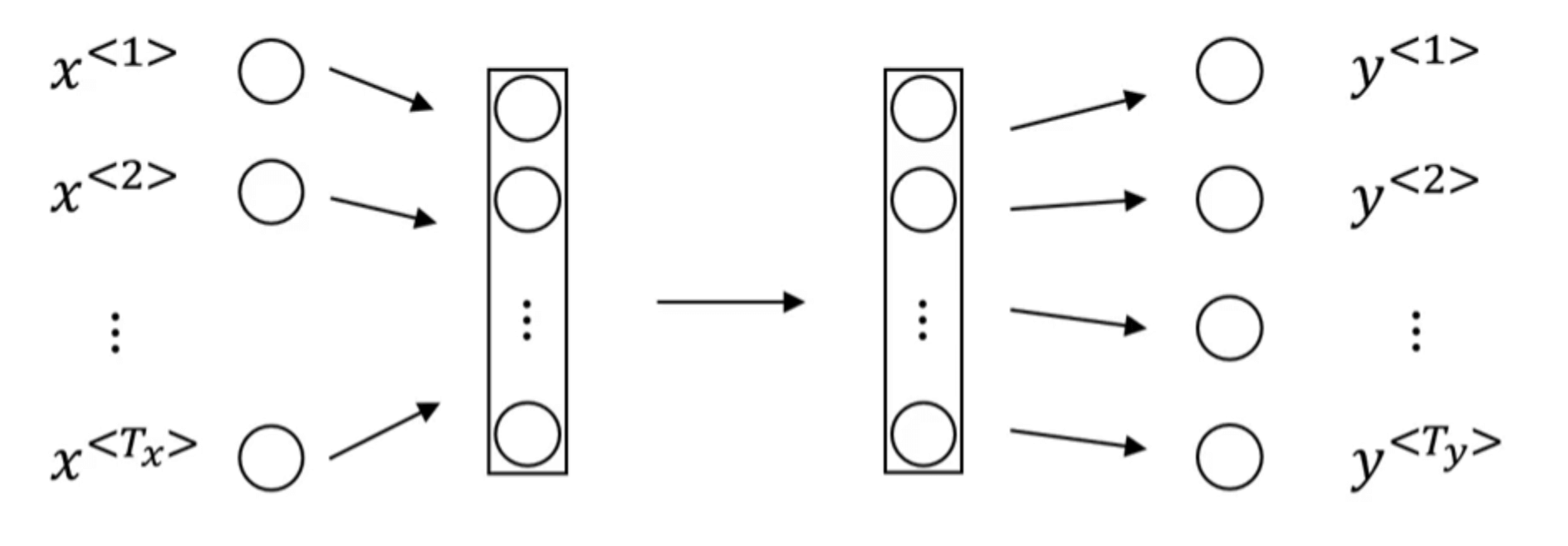
其中,$x^{<n>}$为输入句子中的第n个单词;$y^{<n>}$为第n个单词是否为人名的标识(0或1)。但是这种方法主要会存在两个问题:
- 在不同的样本中,输入$x$和输出$y$可能有不同的长度。即使我们规定了$x,y$的最大长度,对于不满足最大长度的样本进行填充(pad),例如用0填充,使其满足最大长度,但这样依然不是一个好的解决办法。
- 这种传统的标准神经网络结构并不能共享特征之间的信息,即忽视了序列信息,例如句子中前后单词之间的关联。并且模型的参数也会较多。
为了解决这两个问题,我们引入循环神经网络(Recurrent Neural Network,缩写为RNN)。RNN的结构如下图所示:
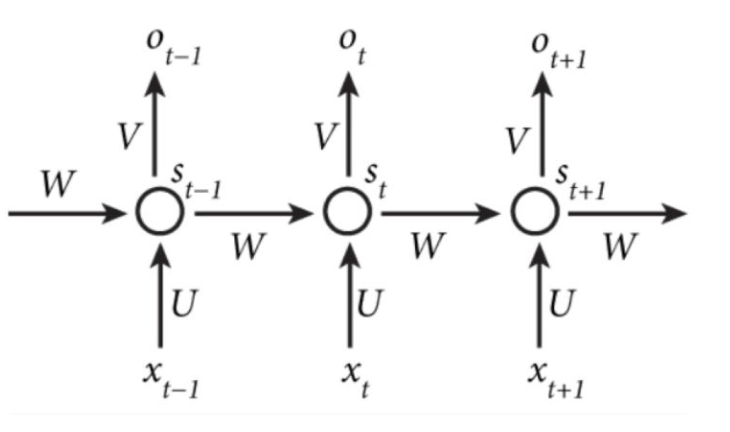
- $O_t=g(V \cdot S_t+b_O)$
- $S_t=f(U \cdot X_t + W \cdot S_{t-1}+b_S)$
其中,$f,g$为不同的激活函数。上述结构也可以简化为:
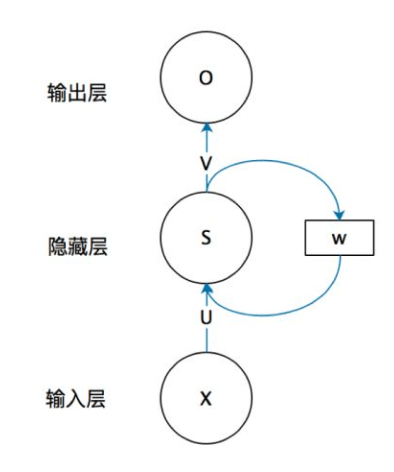
$f$通常为tanh函数(偶尔也用ReLU函数)。
使用RNN模型解决我们之前提到的句子中人名识别的问题:
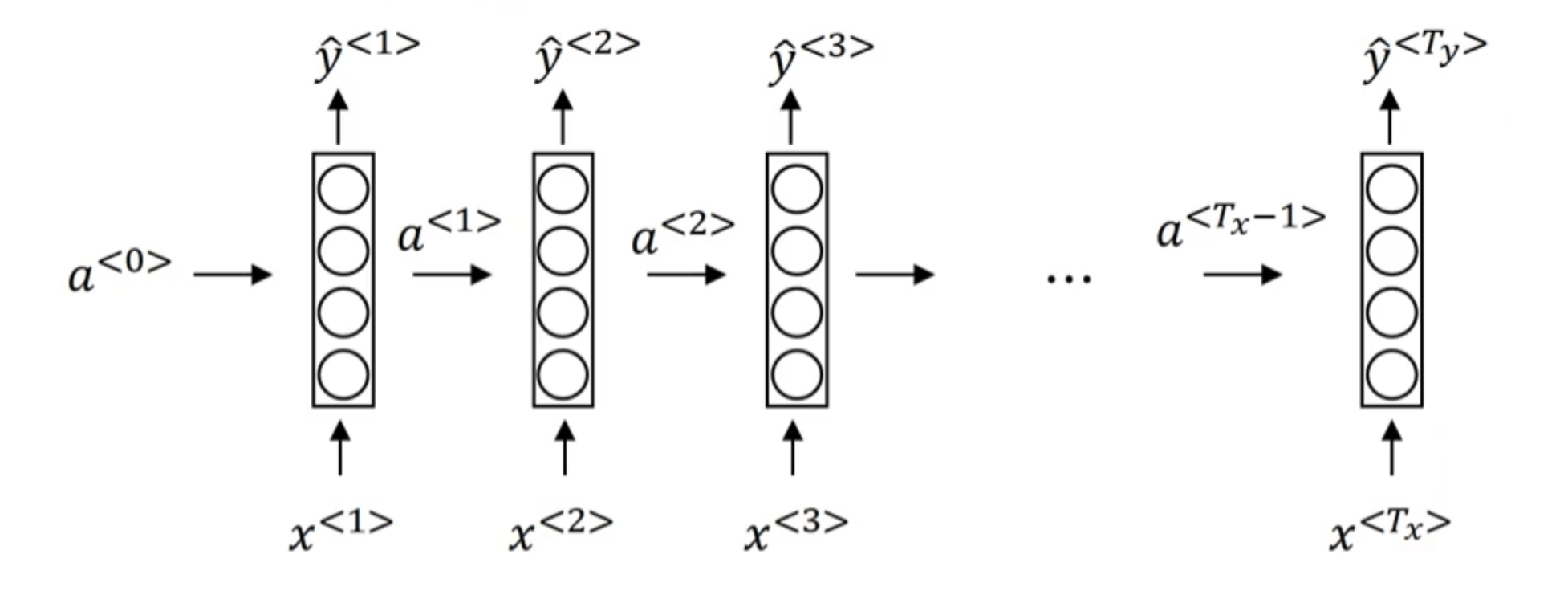
$a^{<0>}$通常被初始化为零向量(或者随机初始化也可以)。比如在预测$\hat{y} ^{<3>}$时,模型会用到$x^{<1>},x^{<2>},x^{<3>}$的信息。
但是这样也有一个弊端:只用到了$x^{<3>}$及其以前的信息。后续博客我们会介绍双向循环神经网络(BRNN)来解决这个问题。
loss function可定义为交叉熵损失函数:
\[L^{<t>}(\hat {y} ^{<t>},y^{<t>})=-y^{<t>} \log \hat {y} ^{<t>} - (1-y^{<t>}) \log (1-\hat {y} ^{<t>})\] \[L(\hat {y},y)=\sum_{t=1}^{T_x} L^{<t>}(\hat {y} ^{<t>},y^{<t>})\]2.更多的RNN框架
第1部分介绍了输入和输出长度一致的RNN框架(Many-to-Many,$T_x=T_y$),本节我们将介绍更多的RNN框架。
- Many-to-One:比如情感分类问题。输入为一段文本,输出为评价等级(例如1星到5星)。
- One-to-Many:比如音乐生成。输入为一种音乐风格,输出为一段音乐。
- Many-to-Many,$T_x \neq T_y$:比如机器翻译。