【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.RNN中的梯度消失问题
以【深度学习基础】第四十一课:RNN应用之语言模型中的语言模型为例,假设我们有句子:“The cat , which …… , was full.”,其中“cat”和“was”需要对应起来。如果使用复数“cats”,则对应的需要使用“were”:“The cats , which …… , were full.”。对于英语来说,“which”后面省略的部分可以是任意长度,因此就需要“cat/cats”和“was/were”之间有长期的依赖关系。但是目前为止,我们所介绍的RNN模型都不擅长捕获这种长期依赖效应。而造成此问题的原因就是梯度消失。
相比于梯度爆炸,梯度消失是训练RNN时的首要问题。尽管梯度爆炸也会出现,但是因为其通常使得网络参数变得过大从而导致网络崩溃,因此,梯度爆炸很容易被发现。解决梯度爆炸的其中一个办法就是梯度修剪。
接下来我们介绍两种可以解决梯度消失,使得RNN可以捕获长期依赖效应的方法:GRU和LSTM。
2.GRU
GRU的全称为Gated Recurrent Unit。
GRU的介绍主要来自以下两篇文章:
Cho K, Van Merriënboer B, Bahdanau D, et al. On the properties of neural machine translation: Encoder-decoder approaches[J]. arXiv preprint arXiv:1409.1259, 2014.
Chung J, Gulcehre C, Cho K H, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[J]. arXiv preprint arXiv:1412.3555, 2014.
GRU的基本结构如下图所示:

假设使用的激活函数为tanh和softmax。
这里我们使用标记“c”表示“memory cell”,其作用便是提供长期记忆的能力。在GRU中,始终有$c^{<t>}=a^{<t>}$。上图中涉及的主要计算见下:
\[\tilde {c}^{<t>}=tanh(W_c [c^{<t-1>},x^{<t>}]+b_c)\] \[\Gamma _u=sigmoid(W_u [c^{<t-1>},x^{<t>}]+b_u)\]使用符号$\Gamma$表示“Gate”(有的资料中也会用$G$表示“Gate”),$\Gamma _u$中的u表示“update”,即控制是否更新$c^{<t>}$。因为计算$\Gamma _u$使用的是sigmoid函数,因此大多数情况下$\Gamma _u$的值都接近1或者0,所以我们使用下式控制$c^{<t>}$的更新:
\[c^{<t>}=\Gamma _u * \tilde {c}^{<t>} + (1-\Gamma _u) * c^{<t-1>}\]如果$\Gamma _u=1$,则相当于更新了$c^{<t>}$;如果$\Gamma _u=0$,则相当于未更新$c^{<t>}$。如果$c^{<t>}$一直不被更新,便可捕获长期依赖效应,例如:
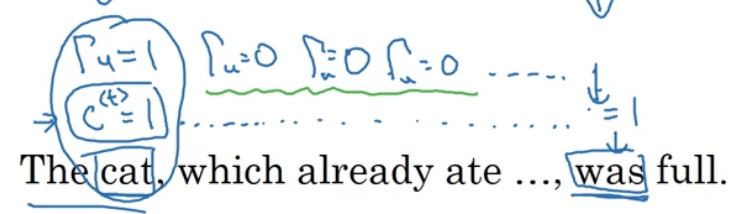
GRU的优点:
- 使用Gate控制memory cell的更新。
- 因为$c^{<t>}$可能会被持续的传递下去,因此解决了梯度消失问题。
以上便是一个简化版的GRU。完整版的GRU是在简化版的基础上新添加了一个Gate:$\Gamma _r$,r表示“relevant”,即$\tilde {c}^{<t>}$和$c^{<t-1>}$之间的相关性。相关修改见下:
\[\tilde {c}^{<t>}=tanh(W_c [\Gamma _r * c^{<t-1>},x^{<t>}]+b_c)\] \[\Gamma _r=sigmoid(W_r [c^{<t-1>},x^{<t>}]+b_r)\]3.LSTM
LSTM的全称为Long Short Term Memory,其比GRU要更为强大和通用。
LSTM出自论文:Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780.
在GRU中,我们规定了$a^{<t>}=c^{<t>}$。而在LSTM中,则没有这个规定。LSTM unit的结构见下:
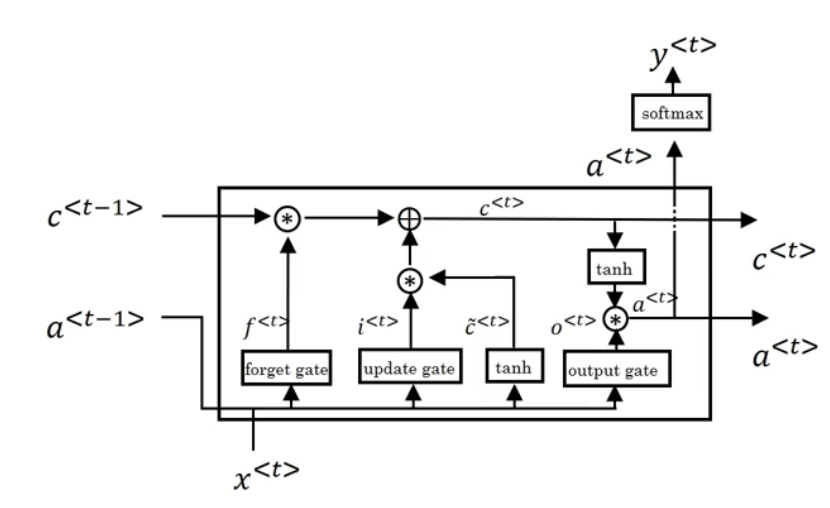
相比GRU,LSTM新增了$\Gamma _f,\Gamma _o$,即“forget gate”和“output gate”。将这些LSTM unit连接起来:

只要正确设置了$\Gamma _u,\Gamma _f$,$c^{<t>}$便可以一直传递下去。此外,最常用的LSTM版本在计算gate时也会将$c^{<t-1>}$考虑在内,这个叫做peephole connection。
什么时候使用GRU,什么时候使用LSTM?这里没有统一的准则。GRU的结构更为简单,更容易创建一个更大的网络,并且只有两个gate,在计算性能上,也会运行的更快。但是LSTM更为强大和灵活。