本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.像素重映射
简单点说,像素重映射就是把输入图像中各个像素按照一定的规则映射到另外一张图像的对应位置上去,形成一张新的图像。例如:

2.相关API
1
2
3
4
5
6
7
8
9
void remap(
InputArray src,
OutputArray dst,
InputArray map1,
InputArray map2,
int interpolation,
int borderMode = BORDER_CONSTANT,
const Scalar& borderValue = Scalar()
);
参数解释:
InputArray src:输入图像。OutputArray dst:输出图像。大小和map1相同,图像类型和src相同。InputArray map1:$x$坐标的映射表或$(x,y)$坐标对的映射表。图像类型可为CV_16SC2、CV_32FC1、CV_32FC2。个人理解:当map1为$x$坐标的映射表时,其图像类型应该是单通道,即CV_32FC1;而当map1为$(x,y)$坐标对的映射表时,其图像类型应该是双通道,即CV_16SC2或CV_32FC2。InputArray map2:$y$坐标的映射表。图像类型可为CV_16UC1、CV_32FC1或者为空(即none,当map1为$(x,y)$坐标对的映射表时,map2可为空)。int interpolation:插值方法。int borderMode:图像边缘处理方式。const Scalar& borderValue:填充边缘所用的像素值。
3.常见的插值方法
在放大图像时,通常需要进行插值操作:
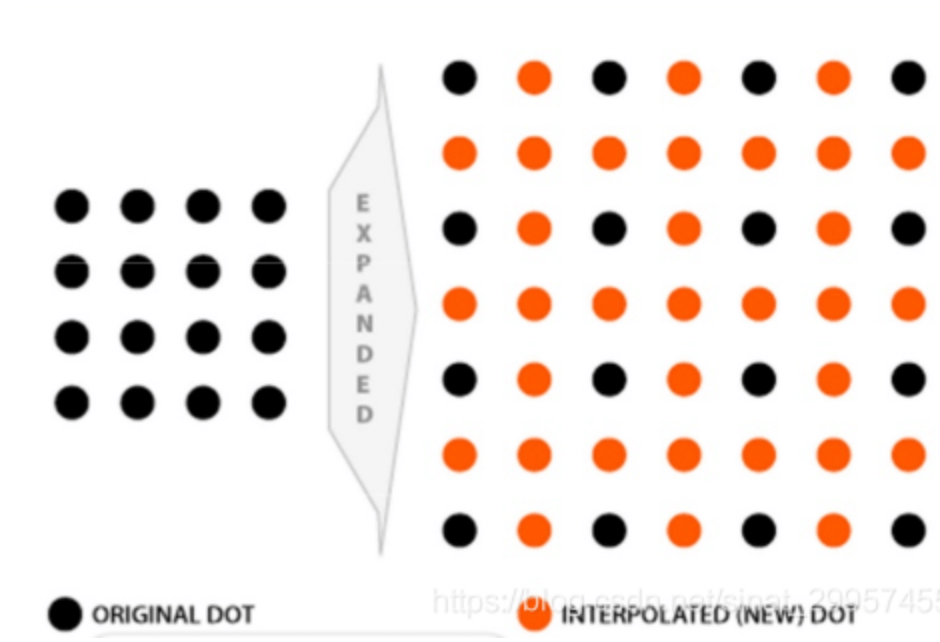
此时我们就需要根据原图中黑色点的像素值推算出插值后图像中橘色点的像素值。橘色点在原图中的坐标可表示为:
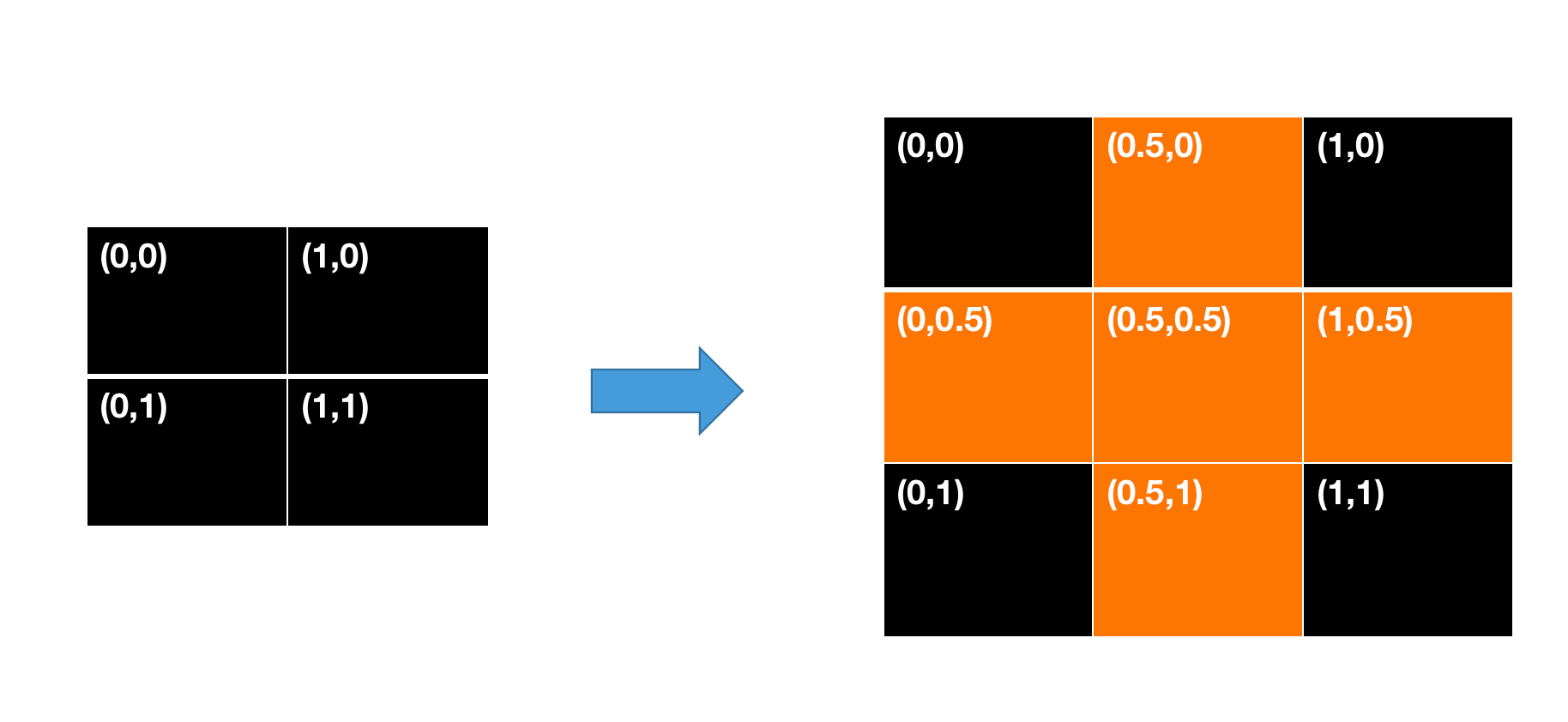
OpenCV提供的插值方法有:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//! interpolation algorithm
enum InterpolationFlags{
/** nearest neighbor interpolation */
INTER_NEAREST = 0,
/** bilinear interpolation */
INTER_LINEAR = 1,
/** bicubic interpolation */
INTER_CUBIC = 2,
/** resampling using pixel area relation. It may be a preferred method for image decimation, as
it gives moire'-free results. But when the image is zoomed, it is similar to the INTER_NEAREST
method. */
INTER_AREA = 3,
/** Lanczos interpolation over 8x8 neighborhood */
INTER_LANCZOS4 = 4,
/** Bit exact bilinear interpolation */
INTER_LINEAR_EXACT = 5,
/** mask for interpolation codes */
INTER_MAX = 7,
/** flag, fills all of the destination image pixels. If some of them correspond to outliers in the
source image, they are set to zero */
WARP_FILL_OUTLIERS = 8,
/** flag, inverse transformation
For example, #linearPolar or #logPolar transforms:
- flag is __not__ set: \f$dst( \rho , \phi ) = src(x,y)\f$
- flag is set: \f$dst(x,y) = src( \rho , \phi )\f$
*/
WARP_INVERSE_MAP = 16
};
3.1.INTER_NEAREST
INTER_NEAREST为最近邻插值,会选择最近的点。
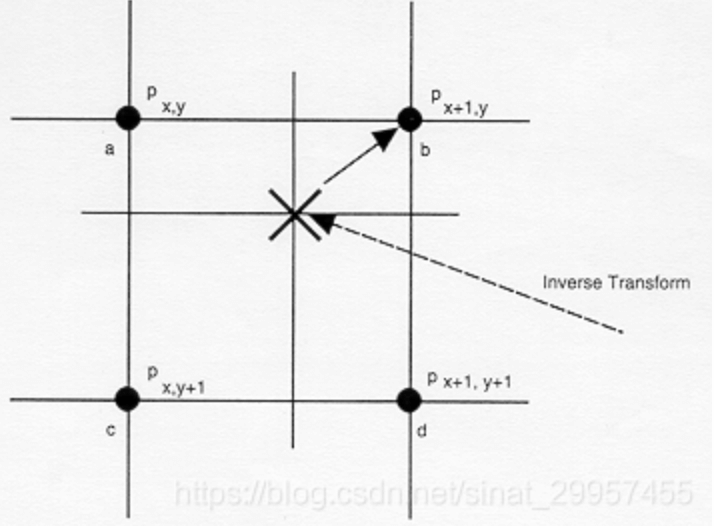
如上图所示,黑色的X表示需要插入的值,它会选择距离它最近的$P_{x+1,y}$的值来作为它的值。
当插入的值距离四个点都相等时,会选择距离最近的左上角的值:
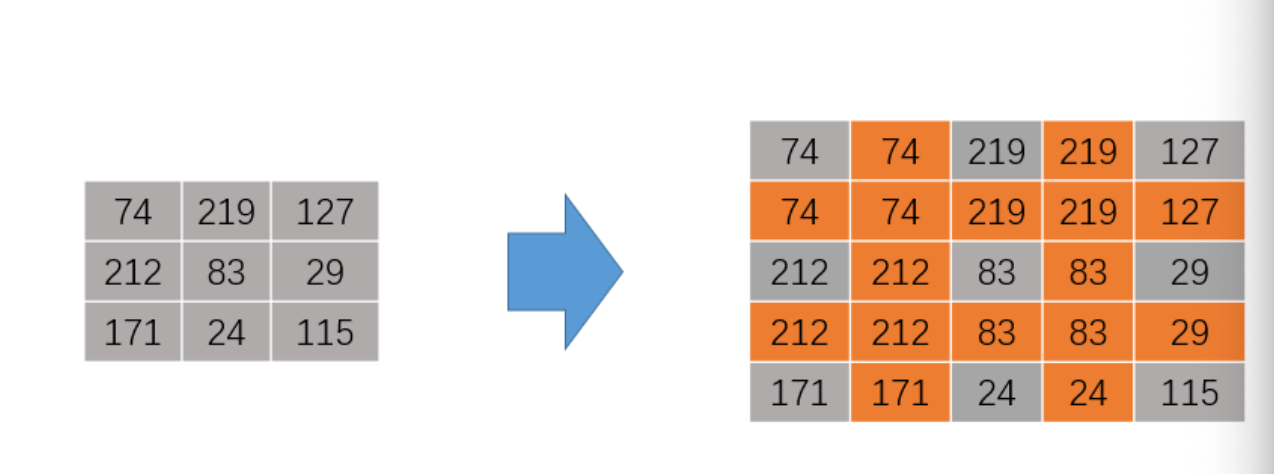
3.2.INTER_LINEAR
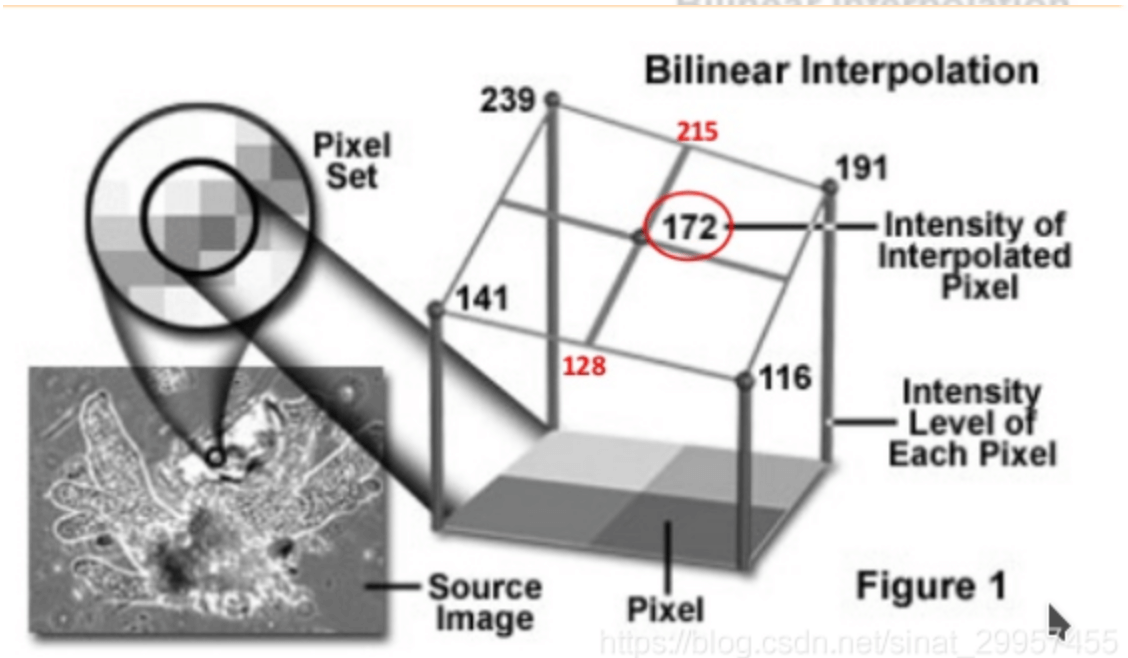
这里的INTER_LINEAR指的是双线性插值。

假设我们想得到未知函数$f$在点$P(x,y)$的值,假设我们已知函数$f$在$Q_{11}=(x_1,y_1),Q_{12}=(x_1,y_2),Q_{21}=(x_2,y_1),Q_{22}=(x_2,y_2)$四个点的值。
先计算函数$f$在点$R_1,R_2$的值:
\[f(R_1) \approx \frac{x_2-x}{x_2-x_1} f(Q_{11})+\frac{x-x_1}{x_2-x_1} f(Q_{21})\] \[f(R_2) \approx \frac{x_2-x}{x_2-x_1} f(Q_{12}) + \frac{x-x_1}{x_2-x_1} f(Q_{22})\]然后估计函数$f$在点$P$的值:
\[\begin{align} f(P) & \approx \frac{y_2-y}{y_2-y_1} f(R_1) + \frac{y-y_1}{y_2-y_1} f(R_2) \\& = \frac{y_2-y}{y_2-y_1} ( \frac{x_2-x}{x_2-x_1} f(Q_{11})+\frac{x-x_1}{x_2-x_1} f(Q_{21}) ) + \frac{y-y_1}{y_2-y_1} ( \frac{x_2-x}{x_2-x_1} f(Q_{12}) + \frac{x-x_1}{x_2-x_1} f(Q_{22}) ) \\&= \frac{1}{(x_2-x_1)(y_2-y_1)} ( f(Q_{11})(x_2-x)(y_2-y) + f(Q_{21})(x-x_1)(y_2-y) + f(Q_{12})(x_2-x)(y-y_1)+f(Q_{22})(x-x_1)(y-y_1) ) \\&= \frac{1}{(x_2-x_1)(y_2-y_1)} \begin{bmatrix} x_2-x & x-x_1 \end{bmatrix} \begin{bmatrix} f(Q_{11}) & f(Q_{12}) \\ f(Q_{21}) & f(Q_{22}) \end{bmatrix} \begin{bmatrix} y_2-y \\ y-y_1 \end{bmatrix} \end{align}\]仔细观察上面的公式不难发现,其实$P$点的值等于周围四个点与$P$点所构成的四个对角矩形面积的加权平均:
3.3.INTER_CUBIC
这里的INTER_CUBIC指的是双三次插值(bicubic interpolation)。双三次插值会考虑周边16个像素的值($4\times 4$)。假设原图中有$4\times 4=16$个像素见下:
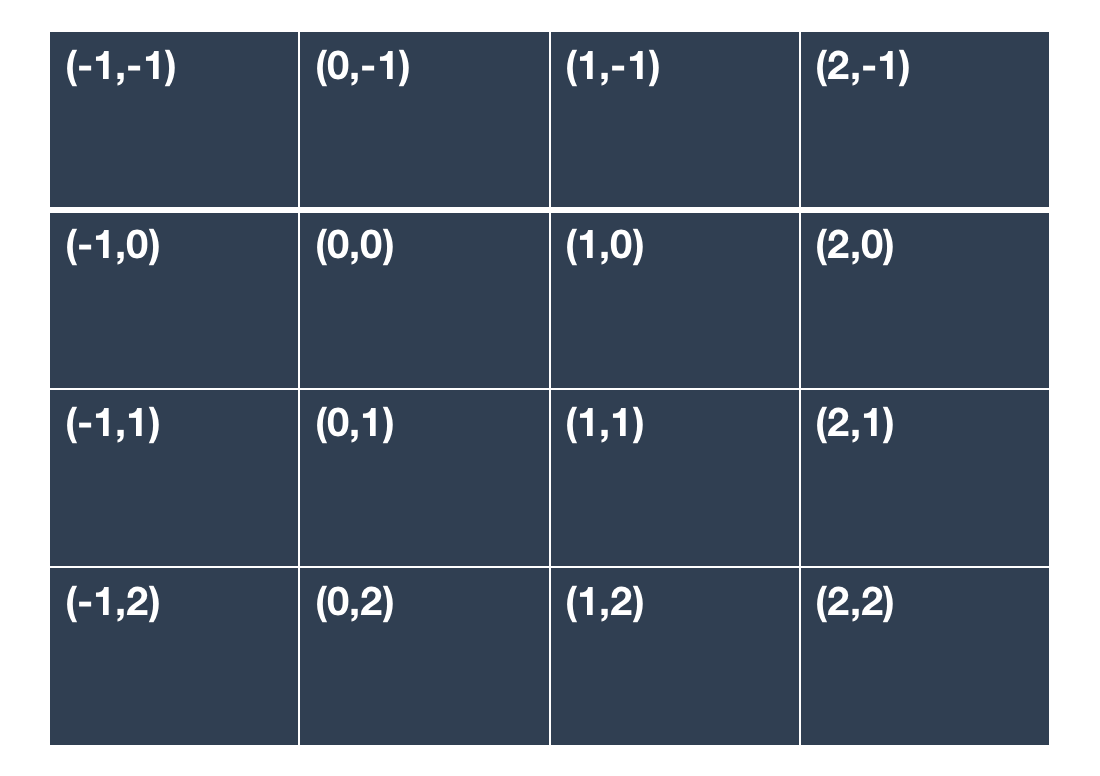
我们用函数$f$表示在某点的像素值,例如$f(0,0)$表示在$(0,0)$位置的像素值。在介绍双三次插值之前先讲解下图像中导数的概念。$(0,0)$位置的一阶偏导数可表示为:
\[f_x(0,0)=\frac{f(0+1,0)-f(0,0)}{1};f_y(0,0)=\frac{f(0,0+1)-f(0,0)}{1}\]但是在双三次插值中,我们使用双边误差更加精确的估计导数:
\[f_x(0,0)=\frac{f(0+1,0)-f(0-1,0)}{2};f_y(0,0)=\frac{f(0,0+1)-f(0,0-1)}{2}\]这也是双三次插值会用到16个像素的原因。除了一阶偏导数,双三次插值还会用到二阶导数(同样使用双边误差估计):
\[f_{xy}(x,y)=\frac{f(x+1,y+1)-f(x+1,y-1)-f(x-1,y+1)+f(x-1,y-1)}{4}\]假设插值后点$(x,y)$的像素值为$p(x,y)$,则$p(x,y)$的计算可表示为:
\[p(x,y)=\sum^3_{i=0} \sum^3_{j=0} a_{ij} x^i y^j\]这便是双三次插值的计算公式。我们只要得到这16个系数$a_{ij}$的值即可。构建以下方程组:
- $f(0,0)=p(0,0)=a_{00}$
- $f(1,0)=p(1,0)=a_{00}+a_{10}+a_{20}+a_{30}$
- $f(0,1)=p(0,1)=a_{00}+a_{01}+a_{02}+a_{03}$
- $f(1,1)=p(1,1)=\sum^3_{i=0} \sum^3_{j=0} a_{ij}$
- $f_x(0,0)=p_x(0,0)=a_{10}$
- $f_x(1,0)=p_x(1,0)=a_{10}+2a_{20}+3a_{30}$
- $f_x(0,1)=p_x(0,1)=a_{10}+a_{11}+a_{12}+a_{13}$
- $f_x(1,1)=p_x(1,1)=\sum^3_{i=1} \sum^3_{j=0} a_{ij} i$
- $f_y(0,0)=p_y(0,0)=a_{01}$
- $f_y(1,0)=p_y(1,0)=a_{01}+a_{11}+a_{21}+a_{31}$
- $f_y(0,1)=p_y(0,1)=a_{01}+2a_{02}+3a_{03}$
- $f_y(1,1)=p_y(1,1)=\sum^3_{i=0} \sum^3_{j=1} a_{ij} j$
- $f_{xy}(0,0)=p_{xy}(0,0)=a_{11}$
- $f_{xy}(1,0)=p_{xy}(1,0)=a_{11}+2a_{21}+3a_{31}$
- $f_{xy}(0,1)=p_{xy}(0,1)=a_{11}+2a_{12}+3a_{13}$
- $f_{xy}(1,1)=p_{xy}(1,1)=\sum^3_{i=1} \sum^3_{j=1} a_{ij} ij$
求导遵循以下公式:
\[p_x(x,y)=\sum^3_{i=1} \sum^3_{j=0} a_{ij} i x^{i-1} y^j\] \[p_y(x,y)=\sum^3_{i=0} \sum^3_{j=1} a_{ij} x^i j y^{j-1}\] \[p_{xy}(x,y) = \sum^3_{i=1} \sum^3_{j=1} a_{ij} i x^{i-1} j y^{j-1}\]假设有:
\[\alpha = [ a_{00} \ a_{10} \ a_{20} \ a_{30} \ a_{01} \ a_{11} \ a_{21} \ a_{31} \ a_{02} \ a_{12} \ a_{22} \ a_{32} \ a_{03} \ a_{13} \ a_{23} \ a_{33} ]^T\] \[x=[f(0,0) \ f(1,0) \ f(0,1) \ f(1,1) \ f_x(0,0) \ f_x(1,0) \ f_x(0,1) \ f_x(1,1) \ f_y(0,0) \ f_y(1,0) \ f_y(0,1) \ f_y(1,1) \ f_{xy}(0,0) \ f_{xy}(1,0) \ f_{xy}(0,1) \ f_{xy}(1,1) ]^T\]上述方程组可解为:$A\alpha =x$或$A^{-1}x=\alpha$,其中$A^{-1}$为:
\[A^{-1}=\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -3 & 3 & 0 & 0 & -2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & -2 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -3 & 3 & 0 & 0 & -2 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & -2 & 0 & 0 & 1 & 1 & 0 & 0 \\ -3 & 0 & 3 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -3 & 0 & 3 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & -1 & 0 \\ 9 & -9 & -9 & 9 & 6 & 3 & -6 & -3 & 6 & -6 & 3 & -3 & 4 & 2 & 2 & 1 \\ -6 & 6 & 6 & -6 & -3 & -3 & 3 & 3 & -4 & 4 & -2 & 2 & -2 & -2 & -1 & -1 \\ 2 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ -6 & 6 & 6 & -6 & -4 & -2 & 4 & 2 & -3 & 3 & -3 & 3 & -2 & -1 & -2 & -1 \\ 4 & -4 & -4 & 4 & 2 & 2 & -2 & -2 & 2 & -2 & 2 & -2 & 1 & 1 & 1 & 1 \\ \end{bmatrix}\]也可以写成如下更为简洁的形式:
\[\begin{bmatrix} f(0,0) & f(0,1) & f_y(0,0) & f_y(0,1) \\ f(1,0) & f(1,1) & f_y(1,0) & f_y(1,1) \\ f_x(0,0) & f_x(0,1) & f_{xy}(0,0) & f_{xy}(0,1) \\ f_x(1,0) & f_x(1,1) & f_{xy}(1,0) & f_{xy}(1,1) \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 2 & 3 \\ \end{bmatrix} \begin{bmatrix} a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13} \\ a_{20} & a_{21} & a_{22} & a_{23} \\ a_{30} & a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \begin{bmatrix} 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ \end{bmatrix}\]或:
\[\begin{bmatrix} a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13} \\ a_{20} & a_{21} & a_{22} & a_{23} \\ a_{30} & a_{31} & a_{32} & a_{33} \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -3 & 3 & -2 & -1 \\ 2 & -2 & 1 & 1 \\ \end{bmatrix} \begin{bmatrix} f(0,0) & f(0,1) & f_y(0,0) & f_y(0,1) \\ f(1,0) & f(1,1) & f_y(1,0) & f_y(1,1) \\ f_x(0,0) & f_x(0,1) & f_{xy}(0,0) & f_{xy}(0,1) \\ f_x(1,0) & f_x(1,1) & f_{xy}(1,0) & f_{xy}(1,1) \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & -3 & 2 \\ 0 & 0 & 3 & -2 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & -1 & 1 \\\end{bmatrix}\]$p(x,y)$的计算也可以写成:
\[p(x,y)=\begin{bmatrix} 1 & x & x^2 & x^3\\ \end{bmatrix} \begin{bmatrix} a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13} \\ a_{20} & a_{21} & a_{22} & a_{23} \\ a_{30} & a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \begin{bmatrix} 1 \\ y \\ y^2 \\ y^3 \\ \end{bmatrix}\]3.3.1.双三次插值的卷积算法
假设原图点$(x,y)$的像素值为$f(x,y)$,则插值后得到$F(x+v,y+u)$($0 \leqslant u,v \leqslant 1$):
\[F(x+v,y+u) = \begin{bmatrix} W(1+v) & W(v) & W(1-v) & W(2-v) \\ \end{bmatrix} \begin{bmatrix} f(x-1,y-1) & f(x-1,y) & f(x-1,y+1) & f(x-1,y+2) \\ f(x,y-1) & f(x,y) & f(x,y+1) & f(x,y+2) \\ f(x+1,y-1) & f(x+1,y) & f(x+1,y+1) & f(x+1,y+2) \\ f(x+2,y-1) & f(x+2,y) & f(x+2,y+1) & f(x+2,y+2) \\ \end{bmatrix} \begin{bmatrix} W(1+u) \\ W(u) \\ W(1-u) \\ W(2-u) \\ \end{bmatrix}\]上式等价于:
\[F(x+v,y+u) = \sum^2_{row=-1} \sum^2_{col=-1} f(x+row,y+col) W(row-v) W(col - u)\]其中,$W(x)$的计算见下:
\[W(x) = \begin{cases} (a+2)\lvert x \rvert ^3 - (a+3) \lvert x \rvert ^2 + 1 & for \ \lvert x \rvert \leqslant 1 \\ a\lvert x \rvert ^3 - 5a\lvert x \rvert ^2 + 8a \lvert x \rvert -4a & for \ 1 < \lvert x \rvert < 2 \\ 0 & otherwise \end{cases}\]$a$通常取-0.5或-0.75。