本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.图像直方图
假设有图像数据$8\times 8$,像素值范围0~14共15个灰度等级:
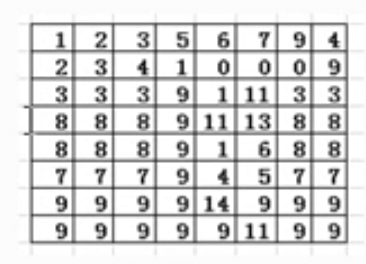
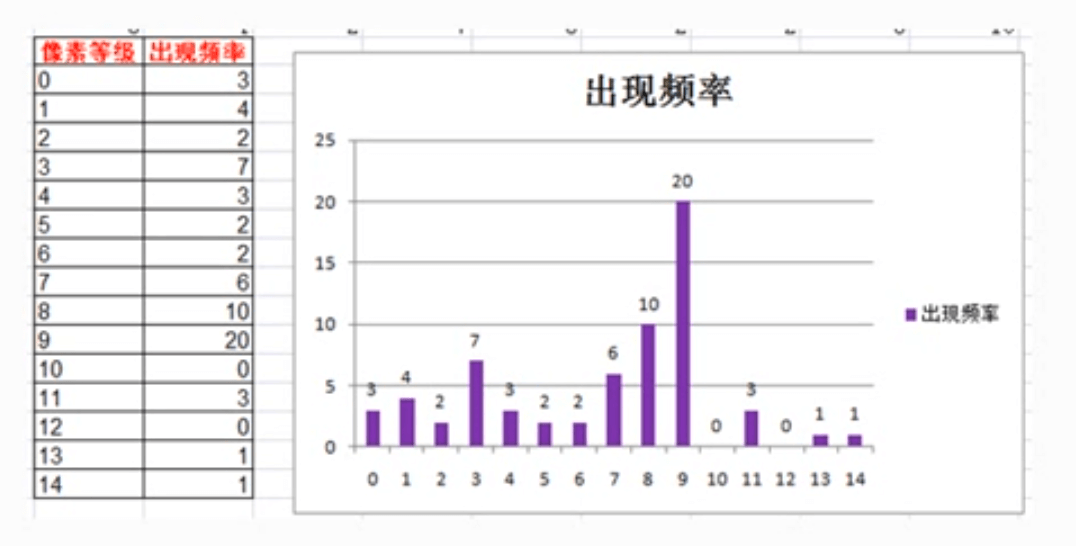
统计得到各个等级出现次数及直方图:
2.直方图均衡化
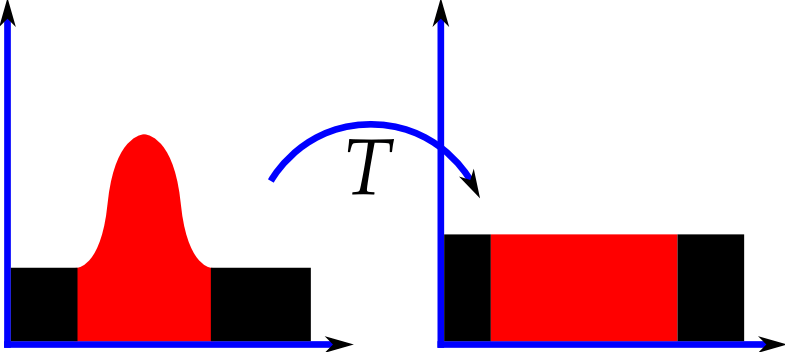
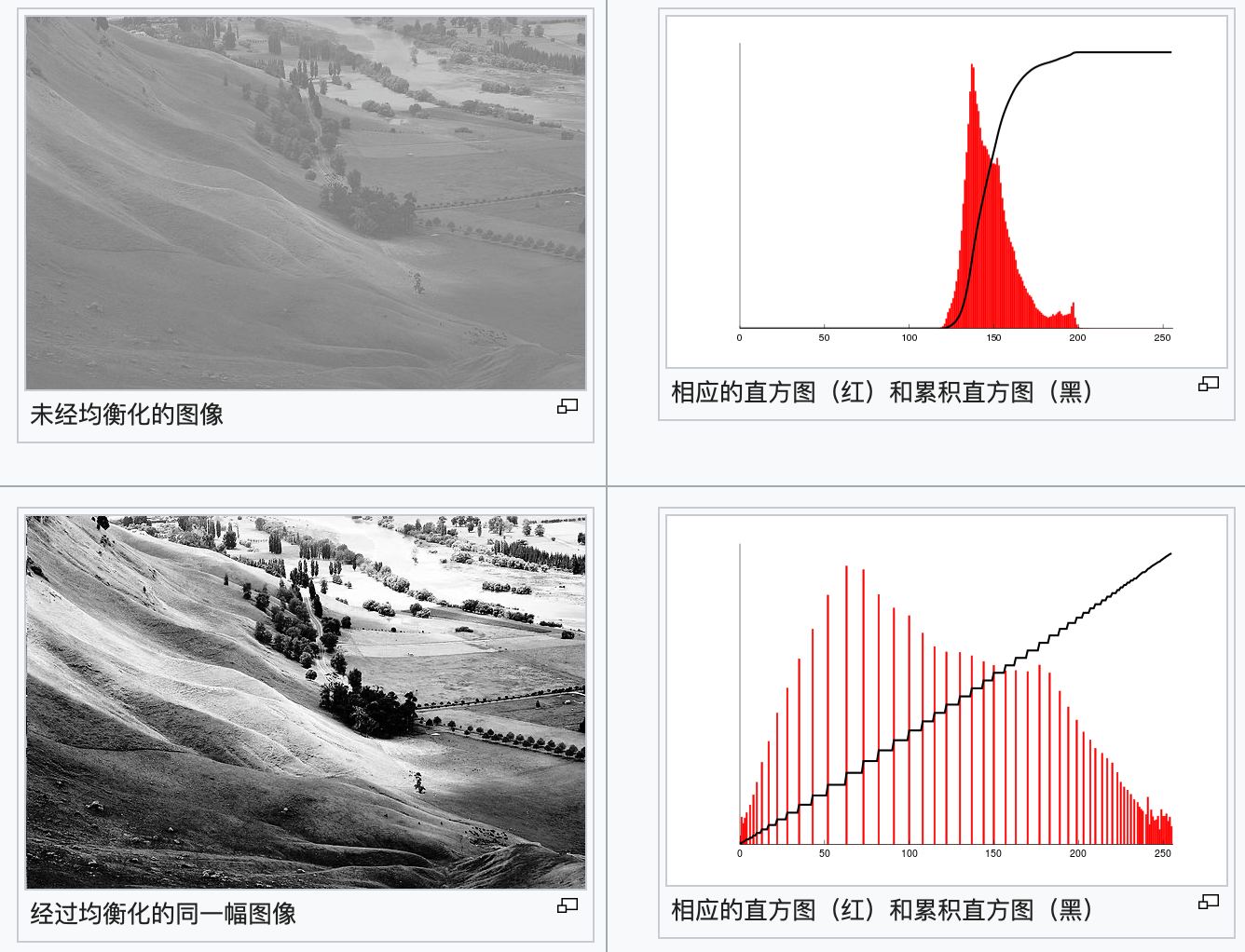
直方图均衡化(Histogram Equalization)是一种增强图像对比度的方法。其主要思想是将一副图像的直方图分布变成近似均匀分布,从而增强图像的对比度。均衡化前后的图像直方图:
举例说明下直方图均衡化的过程,假设现在有一个8位的$8\times 8$灰度图像:
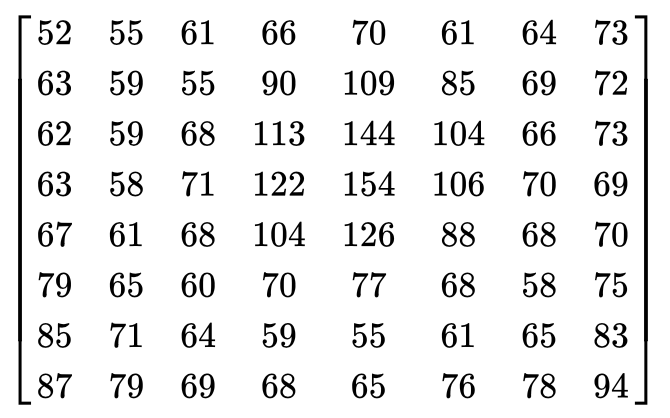
该灰度图像的灰度值出现次数如下表所示,为了简化表格,出现次数为0的值已经被省略:

累积分布函数(cdf)如下所示,与上一表格类似,为了简化,累积分布函数值为0的灰度值已经被省略:
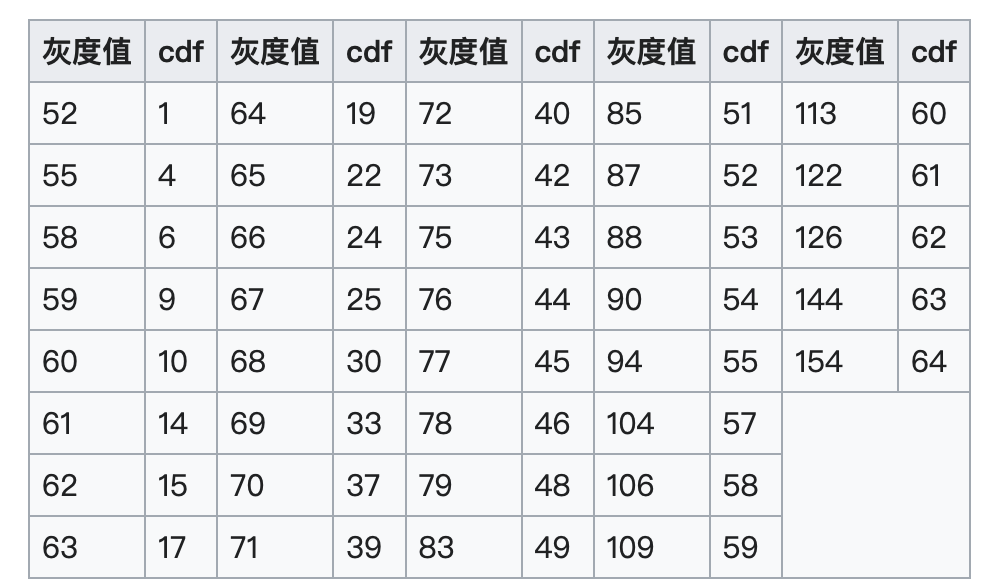
如表格所示,灰度值最小值为52,最大值为154。通常,直方图均衡化算式如下:
\[h(v)=round \left( \frac{cdf(v) - cdf_{min}}{cdf_{max}-cdf_{min}} \times (L-1) \right)\]累积分布函数最小值$cdf_{min}$在本例中为1,最大值$cdf_{max}$在本例中为64,而$L$则是灰度级数(如本例中,图像为8位深度,则灰度级数共有$2^8=256$级数,这也是最常见的灰度级数)。则对于本例的直方图均衡化算式为:
\[h(v)=round \left( \frac{cdf(v)-1}{63} \times 255 \right)\]例如,灰度为78的像素的累积分布函数为46,均衡化后,灰度值变化为:
\[h(78)=round \left( \frac{46-1}{63} \times 255 \right) = round (0.714286 \times 255)=182\]直方图均衡化后,图像的灰度值变化如下表所示:


全尺寸图像效果:
3.API
1
void equalizeHist( InputArray src, OutputArray dst );
⚠️输入图像必须是8位的单通道图像。