【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.半朴素贝叶斯分类器
为了降低贝叶斯公式
\[P(c \mid \mathbf x)=\frac{P(c)P(\mathbf x \mid c)}{P(\mathbf x)} \tag{1}\]中估计后验概率$P(c\mid \mathbf x)$的困难,朴素贝叶斯分类器采用了属性条件独立性假设,但在现实任务中这个假设往往很难成立。于是,人们尝试对属性条件独立性假设进行一定程度的放松,由此产生了一类称为“半朴素贝叶斯分类器”(semi-naive Bayes classifiers)的学习方法。
半朴素贝叶斯分类器的基本想法是适当考虑一部分属性间的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。“独依赖估计”(One-Dependent Estimator,简称ODE)是半朴素贝叶斯分类器最常用的一种策略。顾名思义,所谓“独依赖”就是假设每个属性在类别之外最多仅依赖于一个其他属性,即
\[P(c\mid \mathbf x) \propto P(c) \prod ^d_{i=1} P(x_i \mid c,pa_i) \tag{2}\]$\propto$是“正比于”符号。
其中$pa_i$为属性$x_i$所依赖的属性,称为$x_i$的父属性。此时,对每个属性$x_i$,若其父属性$pa_i$已知,则可采用类似
\[\hat {P} (x_i \mid c)=\frac{\lvert D_{c,x_i} \rvert +1}{\lvert D_c \rvert +N_i} \tag{3}\]的方法来估计概率值$P(x_i \mid c,pa_i)$。于是,问题的关键就转化为如何确定每个属性的父属性,不同的做法产生不同的独依赖分类器。
确定父属性的方法:
- 选择贝叶斯分类器(SBC:Selective Bayesian Classifier)。
- 超父独依赖估计分类器(SPODE:Super Parent ODE)。
- 树增广朴素贝叶斯网络分类器(TAN:Tree Augmented NaiveBayes)。
- 平均独依赖估测器(AODE:Averaged ODE)。
- 加权平均独依赖估测器(WAODE:Weightily Averaged ODE)。
2.一个例子
假设有如下数据集,判断是否为好果:

待预测的样本见下:

计算时使用拉普拉斯修正。
假设属性的依赖关系定义如下:
- 大小的依赖属性为:形状,且属性取值为大时依赖形状为圆形。
- 颜色不存在依赖属性。
- 形状的依赖属性为大小,且属性取值为圆形时依赖大小为大。
先计算先验概率:
\[P(c=好果)=\frac{4+1}{10+2}=\frac{5}{12}\] \[P(c=坏果)=\frac{6+1}{10+2}=\frac{7}{12}\]计算带有依赖属性的类条件概率:
\[P(大小=大 \mid c=好果,形状=圆形)=\frac{2+1}{3+2}=\frac{3}{5}\] \[P(颜色=青色 \mid c=好果)=\frac{0+1}{4+2}=\frac{1}{6}\] \[P(形状=圆形 \mid c=好果,大小=大)=\frac{2+1}{3+2}=\frac{3}{5}\] \[P(大小=大 \mid c=坏果,形状=圆形)=\frac{1+1}{2+2}=\frac{2}{4}\] \[P(颜色=青色 \mid c=坏果)=\frac{5+1}{6+2}=\frac{6}{8}\] \[P(形状=圆形 \mid c=坏果,大小=大)=\frac{1+1}{3+2}=\frac{2}{5}\]因此根据式(2)有:
\[P(c=好果) * P(大小=大 \mid c=好果,形状=圆形) * P(颜色=青色 \mid c=好果) * P(形状=圆形 \mid c=好果,大小=大) = 0.025\] \[P(c=坏果) * P(大小=大 \mid c=坏果,形状=圆形) * P(颜色=青色 \mid c=坏果) * P(形状=圆形 \mid c=坏果,大小=大) = 0.0875\]所以上述待测样本最终被预测为坏果。
3.SPODE
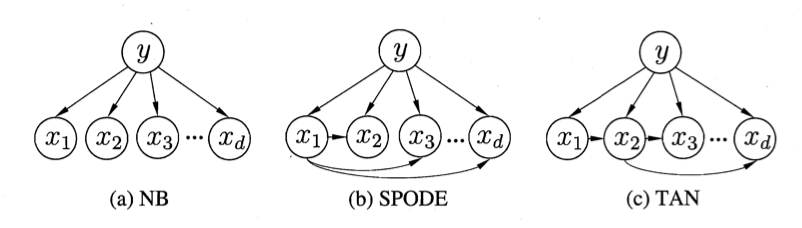
确定父属性最直接的做法是假设所有属性都依赖于同一个属性,称为“超父”(super-parent),然后通过交叉验证等模型选择方法来确定超父属性,由此形成了SPODE(Super-Parent ODE)方法。例如在下图(b)中,$x_1$是超父属性。
4.TAN
TAN(Tree Augmented naive Bayes)是在最大带权生成树(maximum weighted spanning tree)算法的基础上,通过以下步骤将属性间依赖关系约简为如上图(c)所示的树形结构:
最大带权生成树即所有边的权值加起来最大。
1.计算任意两个属性之间的条件互信息(conditional mutual information):
\[I(x_i,x_j \mid y)=\sum_{x_i,x_j;c \in \mathcal{Y}} P(x_i,x_j \mid c) \log \frac{P(x_i,x_j \mid c)}{P(x_i \mid c) P(x_j \mid c)} \tag{4}\]2.以属性为结点构建完全图,任意两个结点之间边的权重设为$I(x_i,x_j \mid y)$。
在图论的数学领域,完全图是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连。
3.构建此完全图的最大带权生成树,挑选根变量,将边置为有向。
4.加入类别节点$y$,增加从$y$到每个属性的有向边。
容易看出,条件互信息$I(x_i,x_j \mid y)$刻画了属性$x_i$和$x_j$在已知类别情况下的相关性,因此,通过最大生成树算法,TAN实际上仅保留了强相关属性之间的依赖性。
5.AODE
AODE(Averaged One-Dependent Estimator)是一种基于集成学习机制、更为强大的独依赖分类器。与SPODE通过模型选择确定超父属性不同,AODE尝试将每个属性作为超父来构建SPODE,然后将那些具有足够训练数据支撑的SPODE集成起来作为最终结果,即:
\[P(c \mid \mathbf x) \propto \sum^d_{\underset {\lvert D_{x_i} \rvert \geqslant m'}{i=1} } P(c,x_i) \prod ^d_{j=1} P(x_j \mid c,x_i) \tag{5}\]$m’$默认设为30。
其中$D_{x_i}$是在第$i$个属性上取值为$x_i$的样本的集合,$m’$为阈值常数,显然,AODE需估计$P(c,x_i)$和$P(x_j \mid c,x_i)$。使用拉普拉斯修正,有:
\[\hat P (c,x_i)=\frac{\lvert D_{c,x_i} \rvert +1}{\lvert D \rvert +N_i} \tag{6}\] \[\hat P (x_j \mid c,x_i) =\frac{\lvert D_{c,x_i,x_j} \rvert +1}{\lvert D_{c,x_i} \rvert + N_j} \tag{7}\]其中$N_i$是第$i$个属性可能的取值数,$D_{c,x_i}$是类别$c$且在第$i$个属性上取值为$x_i$的样本集合,$D_{c,x_i,x_j}$是类别$c$且在第$i$和第$j$个属性上取值分别为$x_i$和$x_j$的样本集合。例如,对西瓜数据集:
6.结语
即然将属性条件独立性假设放松为独依赖假设可能获得泛化性能的提升,那么,能否通过考虑属性间的高阶依赖(即对多个属性依赖)来进一步提升泛化性能呢?也就是说,将式(5)中的属性$pa_i$替换为包含$k$个属性的集合$\mathbf{pa_i}$,从而将ODE拓展为kDE。需注意的是,随着$k$的增加,准确估计概率$P(x_i \mid y, \mathbf{pa_i})$所需的训练样本数量将以指数级增加。因此,若训练数据非常充分,泛化性能有可能提升;但在有限样本条件下,则又陷入估计高阶联合概率的泥沼。