本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
在CV领域中,分割任务的结果通常作为其他任务的基础。所以作者认为分割算法应该满足两个性质:1)能够分割出人类视觉上觉得重要的区域;2)分割速度快,可以实时分割。本分割算法的时间复杂度为$O(n\log n)$,n为图像的像素点个数。
与经典的聚类方法不同,作者用的方法基于图(论)。图的节点为原始图像中的像素点,且相邻的像素点用无向边连接。边的权重为所连接的两个像素点的差异度。并且,与经典方法不同,我们的技术基于图像相邻区域的可变性程度自适应地调整分割标准。
举个例子:
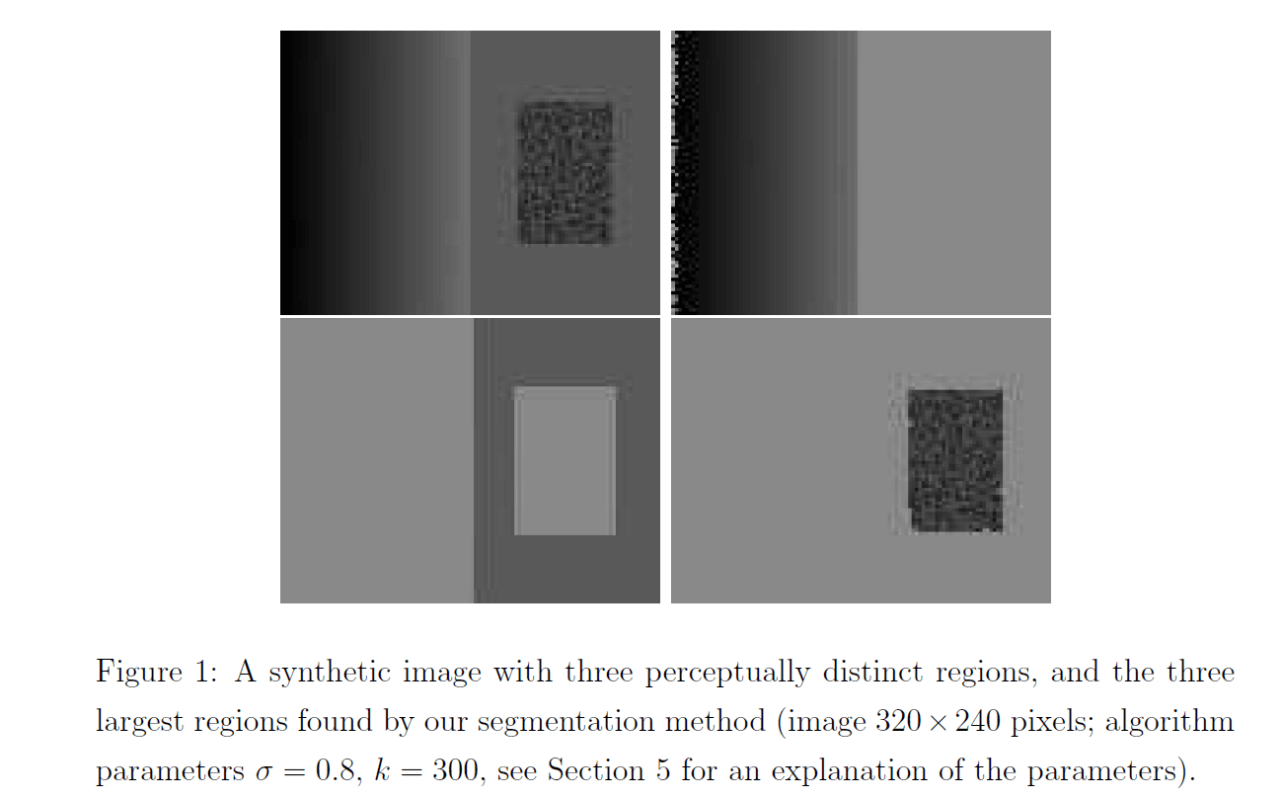
对于Fig1左上角的图像,人类可以很容易的将其视为三个区域:一个矩形像素值渐变的区域(左侧部分);一个矩形像素值恒定的区域(右侧部分);一个像素值变化比较剧烈的区域(右侧小矩形)。这就是我们所说的人类视觉上觉得重要的区域,也是我们希望算法可以分割出来的。这个例子也说明我们不能只依据像素值进行区域的划分。例如左上角图像的左侧区域以及右侧小矩形都有大范围的灰度值变化,但其却应该被视为一个区域,不应被分割。所以作者的方法在判定区域边界时既考虑了边界附近像素值的差异也考虑了区域内部相邻像素点的像素值差异。
Fig1剩余的三幅图像为我们算法分割的结果。
2.Related Work
介绍一些关于图论的基本知识。图可表示为$G=(V,E)$,其中每个节点$v_i \in V$为图像的像素点,$E$为边的集合,连接两个相邻像素点。边的权重基于该边所连接的两个像素点的性质,例如两个像素点的像素值差值。
作者在这一部分提到了使用最小生成树(Minimum Spanning Tree,MST)进行分割。MST中的节点为图像的像素点,边为相邻像素点的连接,边的权值为所连接的两个像素点的像素值的差值(MST常用于点聚类和分割,在点聚类任务中,边的权值为两点间的距离)。使用MST进行分割的核心思想就是切断权值最大的边,这就会出现我们在Fig1中所讨论的问题,边缘的像素值变化小于区域内部,就容易导致将原本是一个的区域划分为多个小区域。
MST是指保证所有节点连通且权值最小的树型结构。MST可以用kruskal算法(见本文第8部分)或prim算法(见本文第9部分)求出。
3.Graph-Based Segmentation
$G=(V,E)$为无向图,节点$v_i \in V$,边$(v_i,v_j) \in E$($v_i,v_j$为相邻节点),边的权重$w((v_i,v_j))$(非负)。
某一分割方式S可将V分为不同子集,即划分为不同的区域C,有$C\in S$,对应的分割结果为$G’=(V,E’)$且有$E’ \subseteq E$(分割后的图在节点上没有变化,依旧是全部的节点,但是某些边会被去掉,这样才能做到分割的效果,所以有$G’=(V,E’)$ 且$E’ \subseteq E$)。有很多不同的方式来衡量分割的质量,我们所用的方式为同一区域内的元素相似度高,而不同区域的元素相似度低。这就意味着同一区域内的边的权值应该较小,而横跨不同区域的边的权值应该较大。
3.1.Pairwise Region Comparison Predicate
单独一个区域C($C \subseteq V$)的内部差异(internal difference)可定义为:
\[Int(C)=\max \limits_{e \in MST(C,E)} w(e) \tag{1}\]两个区域$C_1,C_2$($ C_1, C_2 \subseteq V $)之间的差异可定义为:
\[Dif(C_1,C_2)=\min \limits_{v_i \in C_1,v_j \in C_2,(v_i,v_j)\in E} w((v_i,v_j)) \tag{2}\]如果$C_1,C_2$不相邻,即没有边连接这个区域,则定义$Dif (C_1,C_2)=\infty$。 可以使用下式来决定是否要分割这两个区域(即文中所说的the pairwise comparison predicate):
\[D(C_1,C_2) = \begin{cases} true, & if \ Dif(C_1,C_2) > MInt(C_1,C_2) \\ false, & otherwise \end{cases} \tag{3}\]其中有:
\[MInt(C_1,C_2) = \min (Int(C_1)+\tau (C_1),Int(C_2)+\tau (C_2)) \tag{4}\]阈值函数$\tau$控制两个区域之间的差异必须大于其内部差异的程度。阈值函数$\tau$的定义基于区域C的大小$\mid C \mid$:
\[\tau (C)=k/\mid C \mid \tag{5}\]k是一个超参数。k越大,最终分割出来的区域越少,每个区域的面积就会越大。
区域C的大小可以理解为区域C内像素点的个数。
4.The Algorithm and Its Properties
分割算法的具体实现:
将image转化成graph:$G=(V,E)$,且共有n个节点和m条边。graph是算法的输入,算法的输出是分割结果,即将image分割为多个不同区域:$S=(C_1,…,C_r)$。
节点即为image中的像素点,边即为相邻像素点的连线(每个像素点考虑八邻域),边的权重可以为该边所连接的两个像素点的像素值差值的绝对值。
👉第零步:将边按其权重进行升序排列,得到$\pi=(o_1,…,o_m)$。
👉第一步:将每一个节点视为一个单独的区域,将其作为算法的初始分割$S^0$。
👉第二步:设$q=1,…,m$,循环第三步。
👉第三步:假设第q条边为$o_q=(v_i,v_j)$($v_i,v_j$为该边所连接的两个相邻像素点),节点$v_i$属于区域$C_i^{q-1}$,节点$v_j$属于区域$C_j^{q-1}$,区域$C_i^{q-1}$和区域$C_j^{q-1}$都属于分割$S^{q-1}$。如果$C_i^{q-1} \neq C_j^{q-1}$且$w(o_q) \leqslant M Int (C_i^{q-1},C_j^{q-1})$,则合并区域$C_i^{q-1}$和区域$C_j^{q-1}$,否则不合并(即$S^q=S^{q-1}$)。
👉第四步:遍历完所有的边后,得到最后的分割结果$S^m$。
在第零步中,相同权值的边的排序不会影响到分割结果(原文对此还进行了证明,这里不再详述)。
论文在这一部分还证明了本方法得到的分割结果既没有过分割,也没有欠分割,在此不再赘述。
4.1.Implementation Issues and Running Time
本算法的运行时间主要分为两个部分。第一个部分是第零步的排序,时间复杂度为$O(m\log m)$。另一部分是步骤一至三,其时间复杂度为$O(m \alpha (m))$。
5.Results for Grid Graphs
首先我们先考虑单通道图像(例如灰度图像)。在计算边的权重之前,通常会先进行一次高斯模糊。作者常设高斯模糊的参数$\sigma=0.8$,这个数值既不会引起图像视觉上的更改,还能去除一定的图像噪声。
对于彩色图像,我们将其视为三个单通道图像,针对每个单通道图像都运行一遍算法,所以共运行了三次算法。最终分割结果为三个单通道图像各自分割结果的交集(即两个相邻像素点只有在三个通道图像中都属于同一个区域,这两个相邻像素点在最终分割结果中才算作是在一个区域内)。或者也可以将边的权值设为该边所连接的两个相邻像素点的距离,然后对于彩色图像,只运行一次算法,但是这样得到的结果没有分通道计算得到的结果好。
一些结果见下(分割区域的颜色是随机的):




6.Results for Nearest Neighbor Graphs
该算法也可应用于近邻图领域,本博客不再详述这部分内容。
7.Summary and Conclusions
该算法的运行时间通常为毫秒级。
8.kruskal算法
算法思路:
- 将图中的所有边都去掉。
- 将边按权值从小到大的顺序添加到图中,保证添加的过程中不会形成环。
- 重复上一步直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
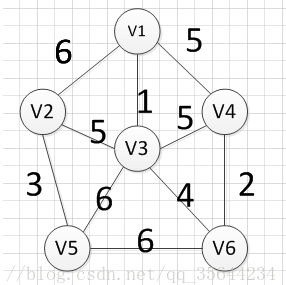
例如针对下图求MST:
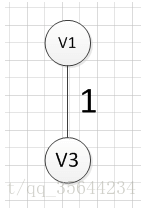
MST的生成步骤见下:
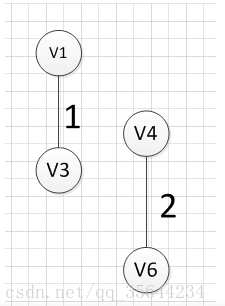
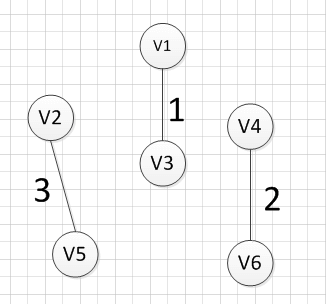
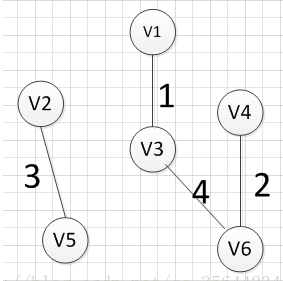
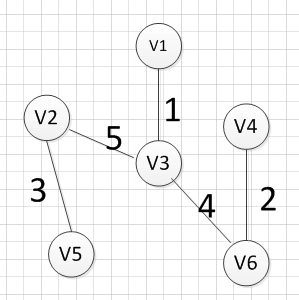
至此,得到MST。
9.prim算法
设有节点集合$U=\{ \}$,从图中任意一个节点$v_a$开始,首先将其放入集合$U$内,即$U=\{ v_a \}$,然后寻找与节点$v_a$所有相关联的边中权值最小的那个,将该边的另一个顶点$v_b$也放入集合$U$,即$U=\{v_a,v_b \}$,然后寻找与节点$v_a$或与节点$v_b$的所有相关联的边中权值最小的那个,同样将该边的另一个顶点放入集合$U$中,如此迭代,直至所有节点都放入$U$中。
例如针对下图求MST:
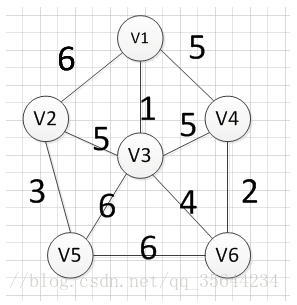
从顶点$v1$开始:
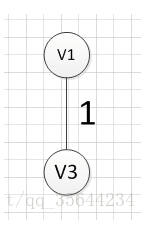
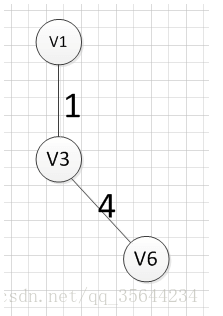
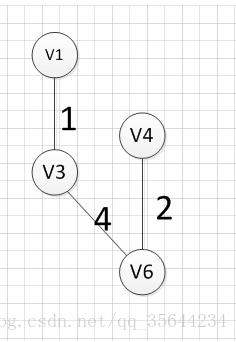

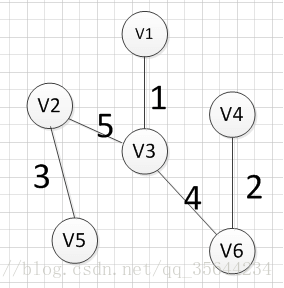
至此,得到MST。
10.原文链接
👽Efficient Graph-Based Image Segmentation