本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
之前写过一篇博客简单的介绍了Batch Normalization:【深度学习基础】第二十三课:Batch Normalization。建议和本文搭配着看。
当神经网络中某一层的输入分布改变时,我们称该层经历了covariate shift。每层固定不变的输入分布有利于高效的训练模型。
把隐藏层输入分布的改变称之为Internal Covariate Shift,将其消除可获得更快的训练速度。
因为网络参数的更新,每一个隐藏层的输入分布在每次迭代时都会不一样,这减慢了训练的速度。
我们提出一种方法,叫Batch Normalization(简称BN),用于降低Internal Covariate Shift,从而实现训练速度的显著提升。同时,该方法也允许我们使用更大的学习率。此外,Batch Normalization还降低了对dropout的需求,并且一定程度上改善了使用sigmoid激活函数出现的梯度消失问题。
2.Towards Reducing Internal Covariate Shift
探索了降低Internal Covariate Shift的一些方式,本部分不再详述。
3.Normalization via Mini-Batch Statistics
假设某一层的输入为d维:$x=(x^{(1)}…x^{(d)})$,我们针对每一维度进行Normalization:
\[\hat{x}^{(k)}=\frac{x^{(k)}-E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}\]归一化至均值为0,方差为1。
但是这样的归一化方式可能会改变该层要表达的内容。比如对于sigmoid激活函数,归一化输入可能会将其限制在函数的线性部分。因此加以改进:
\[y^{(k)}=\gamma^{(k)} \hat{x}^{(k)} + \beta^{(k)}\]如果使用了MBGD,则均值和方差的计算基于一个batch。算法流程见下(称为Batch Normalizing Transform,简称BN Transform):

其中,$\epsilon$为一个常数,$m$为batch size。参数$\gamma,\beta$和网络权值一样,在反向传播过程中会被更新:
\[\frac{\partial \ell}{\partial \hat{x}_i}=\frac{\partial \ell}{\partial y_i} \cdot \gamma\] \[\frac{\partial \ell}{\partial \sigma^2_\mathcal{B}} = \sum^m_{i=1} \frac{\partial \ell}{\partial \hat{x}_i} \cdot (x_i - \mu_{\mathcal{B}})\cdot \frac{-1}{2}(\sigma^2_{\mathcal{B}}+\epsilon)^{-3/2}\] \[\frac{\partial \ell}{\partial \mu_{\mathcal{B}}}=\left( \sum^m_{i=1} \frac{\partial \ell}{\partial \hat{x}_i} \cdot \frac{-1}{\sqrt{\sigma^2_{\mathcal{B}}+\epsilon}} \right)+\frac{\partial \ell}{\partial \sigma^2_{\mathcal{B}}} \cdot \frac{\sum^m_{i=1}-2(x_i-\mu_{\mathcal{B}})}{m}\] \[\frac{\partial \ell}{\partial x_i}=\frac{\partial \ell}{\partial \hat{x}_i} \cdot \frac{1}{\sqrt{\sigma^2_{\mathcal{B}}+\epsilon}}+\frac{\partial \ell}{\partial \sigma^2_{\mathcal{B}}} \cdot \frac{2(x_i-\mu_{\mathcal{B}})}{m} + \frac{\partial \ell}{\partial \mu_{\mathcal{B}}}\cdot \frac{1}{m}\] \[\frac{\partial \ell}{\partial \gamma}=\sum^m_{i=1} \frac{\partial \ell}{\partial y_i} \cdot \hat{x}_i\] \[\frac{\partial \ell}{\partial \beta}=\sum^m_{i=1} \frac{\partial \ell}{\partial y_i}\]3.1.Training and Inference with Batch-Normalized Networks
定义某层的输入为$x$,经过BN后表示为$BN(x)$。
在计算方差时,使用其无偏估计(m为batch size):
\[Var[x]=\frac{m}{m-1} \cdot E_{\mathcal{B}}[\sigma^2_{\mathcal{B}}]\]训练过程见下:

k指的是网络的第k层,一共为K层。
需要注意的是,在训练阶段,我们可以计算每个batch的均值以及方差的移动平均,用于在测试阶段使用。
3.2.Batch-Normalized Convolutional Networks
BN可以应用于网络的任何部分。我们只考虑对激活函数的输入$x$进行BN:
\[z=g(Wu+b)\] \[x=Wu+b\]$g(\cdot)$为非线性激活函数,例如ReLU。如果选择对$u$进行BN($u$其实就是激活函数的输出),其分布形状在训练期间可能会改变,从而影响对covariate shift的消除。相比较而言,$x$的分布更具对称性和非稀疏性。
使用了BN之后,偏置项便可以省略了(因为其会在求平均的时候被消除):
\[z=g(BN(Wu))\]在卷积层中,我们针对每个feature map都训练一组$\gamma,\beta$。
3.3.Batch Normalization enables higher learning rates
在传统的深度网络中,过高的学习率可能会导致梯度消失或梯度爆炸,亦或被卡在局部最小值。BN可以解决这些问题。
3.4.Batch Normalization regularizes the model
作者强调了BN也有正则化作用,所以在使用BN网络的时候,可以不使用或少使用dropout。
4.Experiments
4.1.Activations over time
为了验证BN对internal covariate shift的消除作用,基于MNIST数据集,我们使用了一个简单的网络:输入为$28 \times 28$的二值图像;一共有3个隐藏层且均为全连接;每个隐藏层有100个神经元;激活函数均为sigmoid函数;权值$W$基于高斯分布进行随机初始化;输出层为10个神经元(即10个类别);损失函数使用交叉熵。网络一共训练了50000步,mini-batch size=60。对每个隐藏层都添加了BN。

在Fig1(a)中,纵轴为预测的准确率,横轴为训练步数。可以明显看出,添加了BN之后,网络的准确率更高并且训练速度更快。为了探究造成这个现象的原因,我们研究了最后一个隐藏层中某一神经元的sigmoid函数输入在整个训练过程中的分布变化情况,结果见Fig1(b)和Fig1(c)。三条线分别代表着3个不同的分位数。可以看出,添加BN之后,分布变化较为平稳,这将有助于训练。
4.2.ImageNet classification
我们将BN应用在了GoogLeNet,并在ImageNet2014分类任务数据集上进行训练。详细网络结构见下:
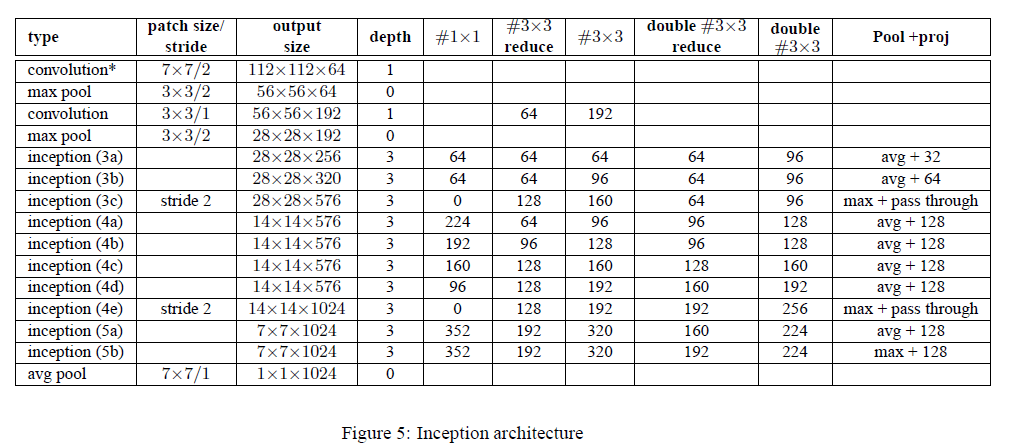
和GoogLeNet主体部分的区别总结如下:
- 将Inception模块中的$5\times 5$卷积层改成了两个连续的$3\times 3$卷积层。所以在Fig(5)中inception模块的深度从2变成了3。
- 在Fig(5)中,第二个卷积层的深度为1。个人觉得这里作者应该是写错了,因为有“#$3\times 3$ reduce”和“#$3\times 3$”,和GoogLeNet是一样的,所以其深度应为2。
- 把部分inception模块中的max pool改为了avg pool。
- 修改了使用的inception模块数量(例如添加了inception3(c))及输出维度。
模型的训练使用momentum梯度下降法,mini-batch size=32。在GoogLeNet中,在测试阶段,我们使用了多个crop的平均结果作为最终预测结果,为了简化,这里我们只使用一个crop。我们将BN应用到了每个非线性激活函数的输入。
4.2.1.Accelerating BN Networks
如果只是单纯的添加BN并不能最大化此方法的效益,因此我们还做了如下改动:
👉Increase learning rate.
我们使用了更大的学习率,并且没有不好的副作用。
👉Remove Dropout.
正如第3.4部分所提到的,BN可以实现和dropout一样的作用。因此在BN-Inception网络中,我们移除了dropout,并且确实也没有出现过拟合的现象。
👉Reduce the L2 weight regularization.
个人理解:L2正则化的$\lambda$值减小了5倍。我们发现这一改动提升了模型准确率。
👉Accelerate the learning rate decay.
因为BN-Inception的训练速度更快,所以我们降低学习率的速度也是GoogLeNet的6倍。
👉Remove Local Response Normalization.
👉Shuffle training examples more thoroughly.
不要让相同的样本总是在一个mini-batch中同时出现。这个改动带来了1%的准确率提升。
👉Reduce the photometric distortions.
减少对原始真实样本的改变(例如常见的一些图像扩展方法:形变、噪声等)。因为训练速度很快,所以我们希望模型在更短的时间内可以聚焦在真实的训练样本上。
4.2.2.Single-Network Classification
我们评估了以下网络,这些网络都在LSVRC2012训练集上进行训练,测试结果基于验证集。
- Inception:见Fig5。初始学习率为0.0015。
- BN-Baseline:在1的基础上,每个非线性激活函数前都使用了BN。
- BN-x5:在2的基础上,添加了第4.2.1部分所提到的修改。其中,初始学习率提升5倍,改为0.0075。
- BN-x30:和3唯一的不同是初始学习率提升了30倍,为0.045。
- BN-x5-Sigmoid:和3唯一的不同是把ReLU激活函数换成了sigmoid激活函数。
测试结果见下图:
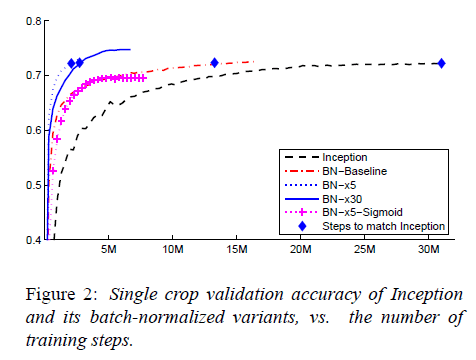
Inception在训练了$31\cdot 10^6$步后达到了72.2%的准确率(Inception所能达到的最高准确率)。BN-Baseline达到72.2%准确率所用的步数不到Inception的一半。BN-x5达到72.2%准确率所用步数仅为Inception的十四分之一。BN-x30相比BN-x5训练速度慢了一些,但是最终的准确率更高,其在$6\cdot 10^6$步时达到了74.8%的准确率。
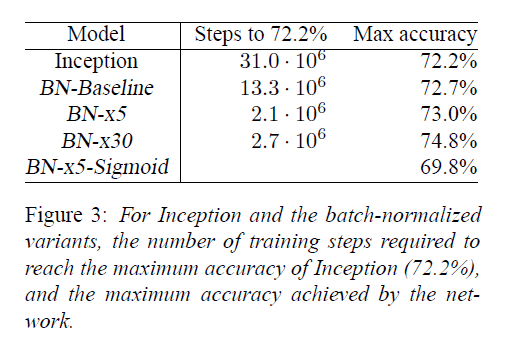
4.2.3.Ensemble Classification

从Fig4可以看出,BN-Inception ensemble取得了比GoogLeNet ensemble更好的结果(基于验证集),甚至在测试集上,BN-Inception ensemble的top-5错误率达到了更低的4.82%。
BN-Inception ensemble所用的6个模型均基于BN-x30,针对每个模型做了以下修改之一:增大卷积层随机初始化的权值;添加dropout(比例为5%或10%,GoogLeNet中使用的是40%);对模型的最后一个隐藏层中的每一个神经元进行BN处理(个人理解:即每个神经元都有一组$\gamma,\beta$,不再是一个feature map共用一个)。
5.Conclusion
BN可以显著的提升深度神经网络的训练速度。并且在此基础上做一些简单的修改,我们可能会获得更好的结果。多个BN模型的集成同样也有助于获得更好的结果。
此外,作者认为BN的潜力还没有被完全开发。在未来的工作中,作者还计划把BN应用于RNN(Recurrent Neural Networks)。
6.原文链接
👽Batch Normalization:Accelerating Deep Network Training by Reducing Internal Covariate Shift