本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
自从AlexNet在ImageNet2012大获成功之后,其就被广泛应用于计算机视觉的诸多领域,例如目标检测、分割、human pose estimation、视频分类以及目标追踪等。
随后,CNN朝着更深更宽(deeper and wider)的方向发展,性能也越来越好,比如后来的VGGNet和GoogLeNet等。
虽然VGGNet的结构简单,但是其计算成本过高。相比之下,GoogLeNet的参数数量只有5M,AlexNet的参数数量为60M,是其12倍,VGGNet的参数数量是AlexNet的3倍多。
Inception网络的计算成本也远低于VGGNet,这使得Inception网络更适合应用于大数据领域。对Inception模块的改进也并非易事,如果只是单纯的扩大其结构,则很有可能导致其计算成本激增。本文提出一些通用的准则和优化策略来改进CNN(并不局限于Inception网络)。
2.General Design Principles
本小节中原则的效用是推测性的,未来需要额外的实验证据来评估其准确性和有效性范围。虽然效用有待进一步验证,但是如果严重偏离这些原则,往往会导致网络质量的恶化。
- 从网络的输入到输出,特征的维度应该是慢慢变小的。我们应当避免特征维度变小的过快,尤其是在网络的前面几层。这样做既可以降低计算量,又不至于损失过多的信息。
- 高维特征更容易被局部处理,更好训练,收敛更快。
- 在低维上进行聚合(concat)既不会损失过多信息(无损压缩或低损压缩),又可以降低计算量。这也是inception模块使用$1\times 1$卷积的原因。
- 平衡网络的宽度和深度。只有按一定比例的增加网络的深度和宽度才能达到网络的最优性能。
3.Factorizing Convolutions with Large Filter Size
GoogLeNet的高性能一部分原因来自于其对降维的大量使用。
3.1.Factorization into smaller convolutions
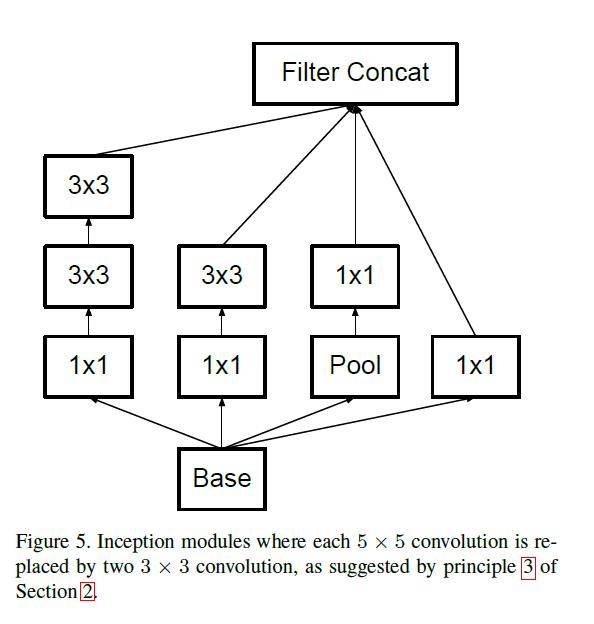
使用较大的卷积核会造成计算成本的显著增加。例如,$5\times 5$卷积核的参数数量是$3\times 3$卷积核参数数量的$25/9=2.78$倍。但是使用大的卷积核可以捕获更多的依赖关系,因此,如果只是单纯的缩小卷积核的尺寸,会造成信息的损失,在一定程度上影响到模型性能。所以我们考虑将一个$5\times 5$的卷积层拆分为两个连续的$3\times 3$卷积层:
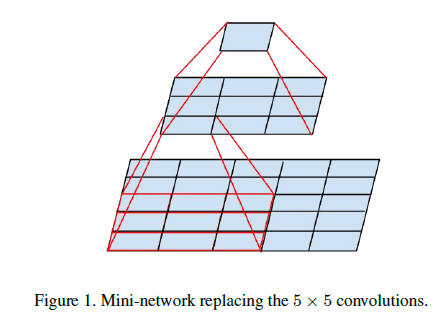
这样既使用了小卷积核来降低计算量(两个$3\times 3$卷积核的参数数量为$9+9=18$,依然小于$5\times 5$卷积核的参数数量),又保证了每个输出神经元的感受野依然是$5\times 5$。
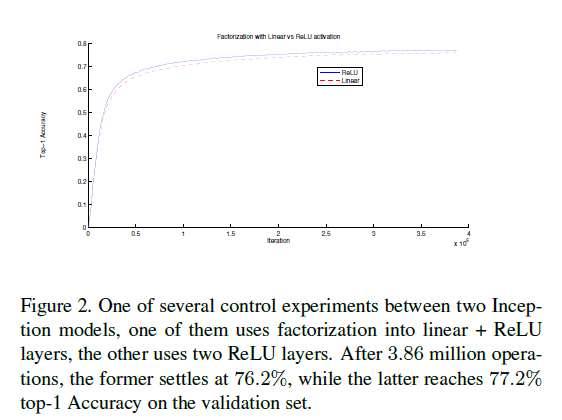
作者还尝试了使用不同的激活函数:一、(分解为两个$3\times 3$卷积层后)第一层使用线性激活函数,第二层使用ReLU激活函数;二、两层都使用ReLU激活函数。从Fig2可以看出,第二种情况的top-1准确率更高。
3.2.Spatial Factorization into Asymmetric Convolutions
基于3.1部分的结果,我们是否可将$3\times 3$卷积核进一步拆分成更小的卷积核呢?答案是可以的,我们在这里尝试使用$n\times 1$这种不对称的卷积核。例如,将$3\times 3$卷积核拆分为$3\times 1$和$1\times 3$两个不对称的卷积核:
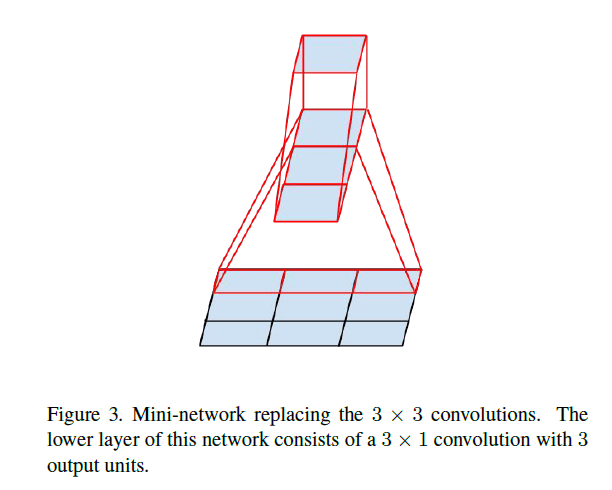
参数数量由9降为6,降低了33%。作为对比,如果将$3\times 3$卷积核拆分为两个$2\times 2$卷积核,仅将参数数量降低了11%(参数数量由9降为8)。
理论上,我们可以用$1\times n$卷积核搭配$n\times 1$卷积核去拆分任意$n\times n$的卷积核,并且n越大,节省的计算成本越显著,例如inception模块可拆分为如Fig6所示:
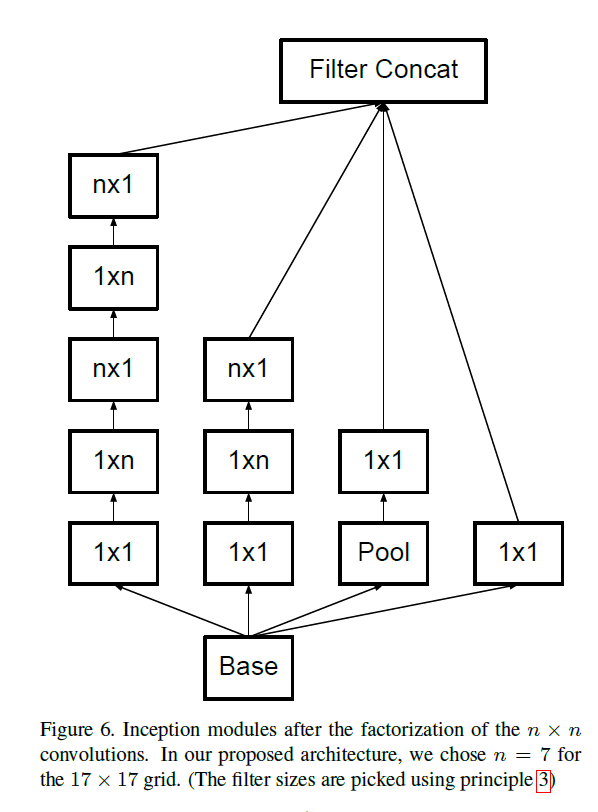
作者还发现,在网络的前几层使用这种拆分策略效果并不好。该拆分策略比较适用于适当大小的feature map(假设feature map的维度为$m\times m$,最好m可以位于12至20之内)。基于这种维度的feature map($12 \leqslant m \leqslant 20$),当n=7时可以获得很好的结果。
Fig6中,m=17,n=7。
4.Utility of Auxiliary Classifiers
在GoogLeNet中还使用了辅助分类器(auxiliary classifiers),目的是为了利用中低层的信息,使训练更快的收敛,解决深层网络的梯度消失问题。但有趣的是,我们发现辅助分类器并没有使训练更快的收敛,但是使用了辅助分类器的网络的最终性能会比不使用辅助分类器的网络的最终性能稍微好那么一点点。
GoogLeNet使用了两个辅助分类器。我们发现移除更浅层的那个辅助分类器对最终结果并没有什么不良影响。作者认为GoogLeNet对辅助分类器的解读并不准确,其并不能很好的提取并利用浅层信息。这些辅助分类器反倒更像是正则化器(regularizer),在辅助分类器中使用BatchNorm或dropout会提升主分类器的性能。
5.Efficient Grid Size Reduction
CNN通常使用pooling来降低feature map的grid size(即维度)。并且在pooling层前,我们通常会进行padding+卷积的操作,以防止feature map的维度降低的太快,从而出现representational bottleneck。举个例子,假设grid size为$d\times d$,有k个卷积核(可理解为feature map的维度为$d\times d \times k$),现在想要得到$\frac{d}{2} \times \frac{d}{2} \times 2k$的维度,有两种方式降维:1)先卷积后pooling(见Fig9右图);2)先pooling后卷积(见Fig9左图)。
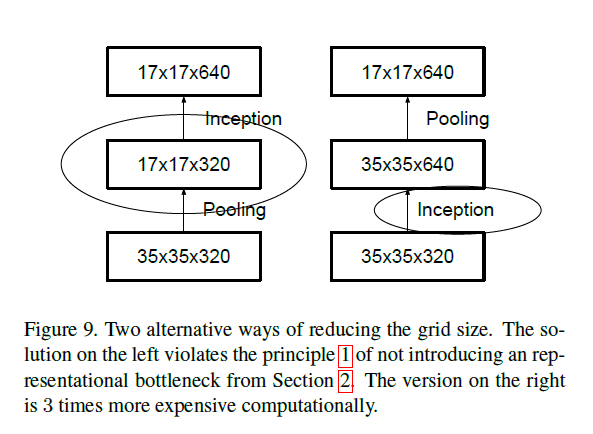
对于方式1,其计算量(因为卷积操作是计算量的主要占比,所以此处只考虑卷积操作的计算量)为$2d^2 m^2 k^2$(假设padding=SAME,卷积核大小为$m\times m$,stride=1,下同);对于方式2,其计算量为$\frac{1}{2} d^2 m^2 k^2$。很明显,方式2的计算量更小,仅为方式1的四分之一,但是方式2违背了原则1(见第2部分)。为了兼顾计算量和原则1,我们提出了以下框架:
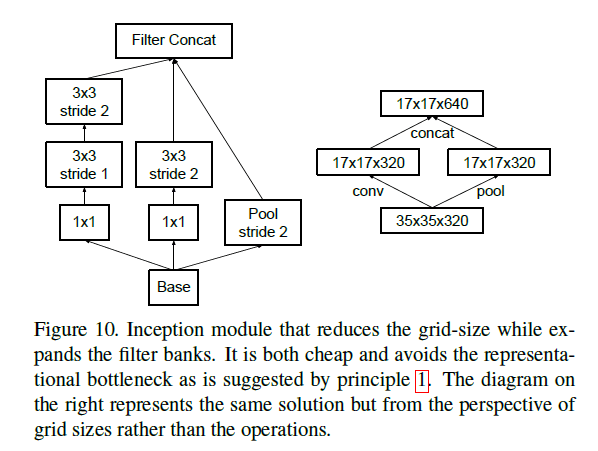
在Fig10右图中,我们创立了两个并行的分支:P(表示pooling层,stride=2)和C(表示卷积层,stride=2)。Fig10左图的inception模块,同样也是兼顾了计算量和原则1的一种实现方式。
个人理解:这部分可以看作是作者对inception模块中pooling和卷积并行的一种解释。
6.Inception-v2
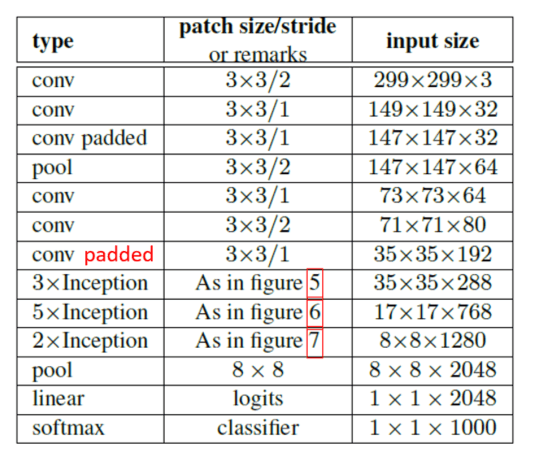
基于ILSVRC2012分类任务的benchmark,我们给出一种新的优化框架见Table1:
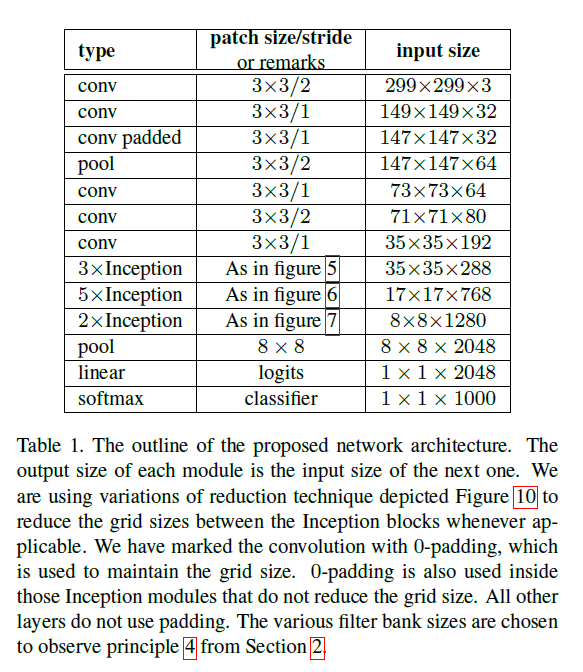
在该框架中,标记padded的地方以及inception模块内部的padding方式均为SAME(且均用0填充)。该框架的构建也兼顾了原则4(见第2部分)。
Table1中,在3$\times $Inception的上一行,这里应该是conv padded,因为这一层的输入为$35 \times 35 \times 192$,卷积核为$3\times 3$,步长为1,如果不做padding,输出应该为$33 \times 33 \times 288$。
我们将$7\times 7$的卷积拆分为三个$3\times 3$的卷积。该框架使用了三种inception模块:
- 见Fig5。因为inception模块内部均使用padding=SAME,所以在经历了3个inception模块后,输出维度应该是$35 \times 35 \times 768$,个人理解这里是用了一个“$3\times 3/2$”的pooling将维度最终降到了$17 \times 17 \times 768$。另一种可能:这3个inception模块的最后一个并不和Fig5完全一样,而是借用了Fig10左图的思想进行改造,以达到降维的目的,例如:
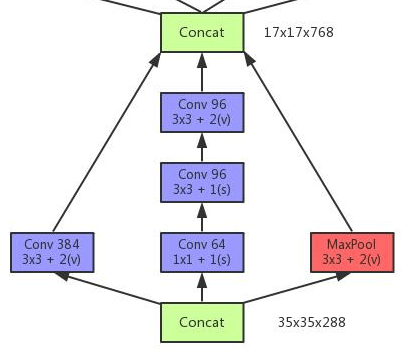
- 见Fig6。其中,$n=7$,padding=SAME。最后也是通过一个“$3\times 3/2$”的pooling将维度降到$8 \times 8 \times 1280$。这里同样存在另一种可能性,例如:
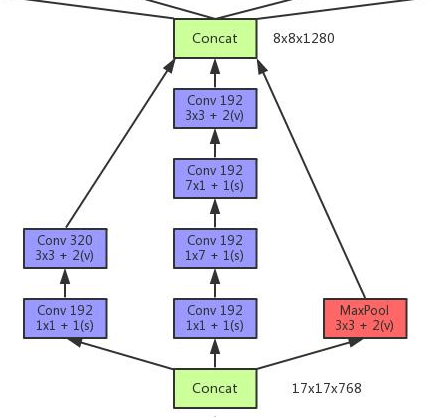
- 见Fig7。

并且,作者发现只要遵守第2部分提到的原则,网络质量就会比较稳定。虽然该框架有42层,并且计算量是GoogLeNet的2.5倍多,但是其相比VGGNet仍然是很高效的。
作者称该框架为“Inception-v2”。
所以Inception-v2指的不是某一inception模块的变体,而是一个网络框架,里面包含多种inception模块及其变体。
7.Model Regularization via Label Smoothing
这里我们提出一种通过标签平滑来正则化网络输出的方法。
对于每个训练样本$x$,网络会输出其属于每个类别$k \in \{ 1…K \}$的概率:$p(k \mid x)=\frac{exp(z_k)}{\sum^K_{i=1}exp(z_i)}$。 样本$x$的真实标签为$q(k\mid x)$,其等于1或者0,且有$\sum_k q(k\mid x)=1$。所以交叉熵损失函数可表示为:$\ell = -\sum^K_{k=1} \log (p(k))q(k)$(其中,$p(k\mid x),q(k\mid x)$简化表示为$p(k),q(k)$)。梯度计算:$\frac{\partial \ell}{\partial z_k}=p(k)-q(k)$(推导过程请见:【深度学习基础】第二十四课:softmax函数的导数),其取值在-1到1之间。
但是上述传统的交叉熵损失函数存在一个问题:损失函数只关注预测正确标签的位置上的概率值。即模型只考虑增大预测正确标签的概率,而不考虑如何减少预测错误标签的概率,这容易导致过拟合,使得模型泛化能力差。
标签平滑正则化(label-smoothing regularization,简称LSR)的实现方法见下式:
\[q'(k \mid x)=(1-\epsilon) \delta_{k,y}+\epsilon u(k)\]通过一个例子来解释上式中各项的含义。假设一共有5个类别,某一样本的ground truth为[0,0,0,1,0](即上式中的$\delta_{k,y}$),经过softmax函数得到的结果为[0.1,0.1,0.1,0.36,0.34]。$\epsilon$为平滑因子,假设有$\epsilon=0.1$,$u(k)$是人为引入的一个固定分布,假设其为[1,1,1,1,1],则经过平滑后的标签$q’(k\mid x)$:
\[\begin{align} q’(k\mid x) &= (1-0.1)\cdot [0,0,0,1,0] + 0.1 \cdot [1,1,1,1,1] \\&= [0,0,0,0.9,0] + [0.1,0.1,0.1,0.1,0.1] \\&= [0.1,0.1,0.1,1.0,0.1] \end{align}\]交叉熵损失可计算为:
\[\begin{align} loss&=-y \log p \\&= -[0.1,0.1,0.1,1.0,0.1] \cdot \log ([0.1,0.1,0.1,0.36,0.34]) \\&= 2.63 \end{align}\]如果不使用LSR,得到的交叉熵为1.47。可以看出,平滑过后的样本交叉熵损失就不仅考虑到了训练样本中正确的标签位置(one-hot标签为1的位置)的损失,也稍微考虑到其他错误标签位置(one-hot标签为0的位置)的损失,导致最后的损失增大,导致模型的学习能力提高,即要下降到原来的损失,就得学习的更好,也就是迫使模型往增大正确分类概率并且同时减小错误分类概率的方向前进。
在原文中,作者设置$u(k)=1/K, \epsilon=0.1$,其中K为类别数。
LSR使模型的top-1和top-5错误率均下降了0.2%左右。
8.Training Methodology
作者使用了TensorFlow框架,训练方法为MBGD,batch size=32,epoch=100。分别尝试了momentum($decay=0.9$)和RMSProp($decay=0.9,\epsilon=1.0$)。学习率的衰减采用指数衰减法,初始学习率为0.045,底数为0.94,每两个epoch衰减一次。此外,作者还使用了梯度裁剪(gradient clipping),阈值设为2.0。
梯度裁剪原文:R. Pascanu, T. Mikolov, and Y. Bengio. On the difficulty of training recurrent neural networks. arXiv preprint arXiv:1211.5063, 2012.。
梯度裁剪能将网络权重有效的控制在一定范围之内,可以有效的解决梯度爆炸问题。
9.Performance on Lower Resolution Input
在目标检测任务之后,我们通常需要将bounding-box框出的目标进行进一步分类(相当于将原始图像的一个小patch作为模型输入进行分类任务)。这种分类问题有个难点就是输入图像尺寸通常较小且分辨率较低。
一般认为,高分辨率的图像会显著提升模型的识别性能。但是高分辨率的图像也会导致计算量的增加(高分辨率相当于输入的维度变大了)。一个折中的想法就是使用低分辨率的图像,尽可能的达到高分辨图像训练出来的模型的性能,并且尽量不修改过多的网络结构。作者实验了3种情况:
- 对于$299 \times 299$的感受野(可简单理解为输入图像的维度),设置步长为2,第一个卷积层后跟一个max-pooling。
- 对于$151 \times 151$的感受野,设置步长为1,第一个卷积层后也跟一个max-pooling。
- 对于$79 \times 79$的感受野,同样设置步长为1,第一个卷积层后不跟pooling。
上述3种情况得到的输出维度是一样的,计算量也差不多。将其均训练至收敛,在ILSVRC2012上的结果见下:
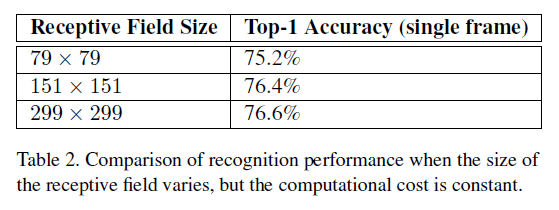
从Table2可以看出,第3种情况的准确率已经相当接近第1种情况了。但是如果针对低分辨率的图像,只是简单的缩小网络的size可能会导致性能的大幅下滑。
10.Experimental Results and Comparisons
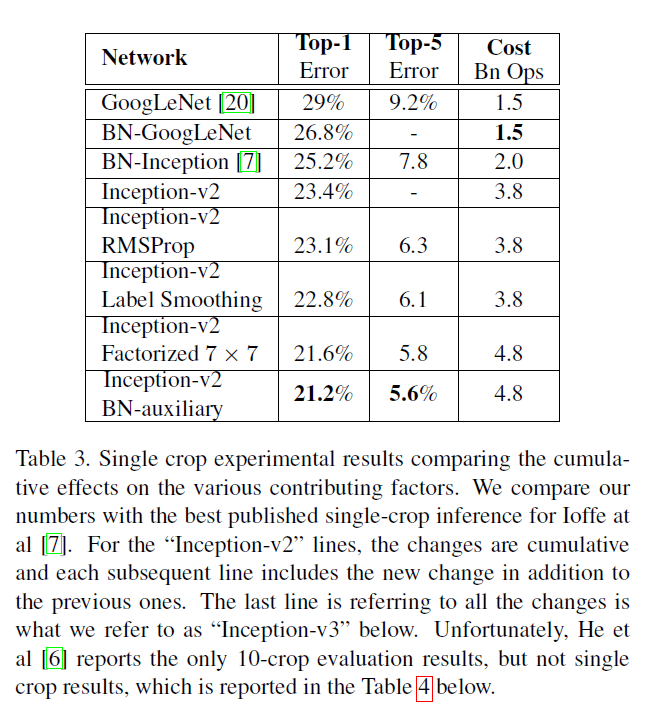
在第6部分介绍的inception-v2的实验结果见Table3。每一行的inception-v2结构都相较前一行累加了一个新的修改。
个人的一些疑惑(但是并不影响理解这篇文章的核心思想):
在第6部分的inception-v2中,$7\times 7$的卷积已经被拆分为3个$3\times 3$卷积了,所以对Table3中的“Inception-v2 Factorized $7\times 7$”有些困惑。这里看起来貌似Table3中的“inception-v2”一行所指的模型并没有将$7\times 7$的卷积拆分。
文章对Table3中的“BN-GoogLeNet”也没有详细的介绍。在Batch Normalization:Accelerating Deep Network Training by Reducing Internal Covariate Shift一文中也只提到了BN-Inception,没有BN-GoogLeNet。个人猜测BN-GoogLeNet应该指的是对原始的GoogLeNet网络(不做任何修改)添加BN(在每一个非线性激活函数前都添加,包括辅助分类器)。
关于Table3中的“Inception-v2 BN-auxiliary”,作者也只是提到对辅助分类器(CONV和FC)进行了BN。不太清楚是否对网络的主体部分也进行了BN操作。此外,针对所有的Inception-v2及其变体,根据作者在第4部分对辅助分类器的解读,很可能会去掉浅层的辅助分类器,只保留深层的那个。
作者将Table3最后一行最优的inception网络称之为inception-v3(即inception-v2+RMSProp+LSR+BN-auxiliary)。Table3的结果是基于single-crop的,multi-crop的测试结果见Table4:
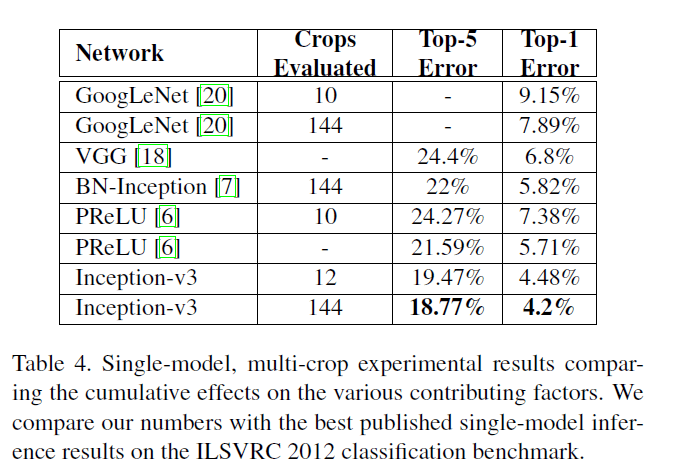
多个模型集成的测试结果见Table5:

评估结果统一基于ILSVRC-2012的验证集。
11.Conclusions
对全文的总结,不再详述。
12.原文链接
👽Rethinking the Inception Architecture for Computer Vision