【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.距离计算
对于【机器学习基础】第三十三课:聚类之性能度量中的函数$dist(\cdot,\cdot)$,若它是一个“距离度量”,则需满足一些基本性质:
- 非负性:$dist(\mathbf{x_i},\mathbf{x_j}) \geqslant 0$
- 同一性:$dist(\mathbf{x_i},\mathbf{x_j}) = 0$当且仅当$\mathbf{x_i}=\mathbf{x_j}$
- 对称性:$dist(\mathbf{x_i},\mathbf{x_j}) =dist(\mathbf{x_j},\mathbf{x_i})$
- 直递性:$dist(\mathbf{x_i},\mathbf{x_j}) \leqslant dist(\mathbf{x_i},\mathbf{x_k}) + dist(\mathbf{x_k},\mathbf{x_j})$
直递性常被直接称为“三角不等式”。
“距离度量”最常用的是“闵可夫斯基距离”。
我们常将属性划分为“连续属性”(continuous attribute)和“离散属性”(categorical attribute),前者在定义域上有无穷多个可能的取值,后者在定义域上是有限个取值。然而,在讨论距离计算时,属性上是否定义了“序”关系更为重要。例如定义域为$\{1,2,3\}$的离散属性与连续属性的性质更接近一些,能直接在属性值上计算距离:“1”与“2”比较接近、与“3”比较远,这样的属性称为“有序属性”(ordinal attribute);而定义域为$\{飞机,火车,轮船\}$这样的离散属性则不能直接在属性值上计算距离,称为“无序属性”(non-ordinal attribute)。显然,闵可夫斯基距离可用于有序属性。
连续属性亦称“数值属性”(numerical attribute),“离散属性”亦称“列名属性”(nominal attribute)。
对无序属性可采用VDM(Value Difference Metric)。令$m_{u,a}$表示在属性$u$上取值为$a$的样本数,$m_{u,a,i}$表示在第$i$个样本簇中在属性$u$上取值为$a$的样本数,$k$为样本簇数,则属性$u$上两个离散值$a$与$b$之间的VDM距离为:
\[VDM_p(a,b) = \sum^k_{i=1} \lvert \frac{m_{u,a,i}}{m_{u,a}} - \frac{m_{u,b,i}}{m_{u,b}} \rvert ^p \tag{1}\]于是,将闵可夫斯基距离和VDM结合即可处理混合属性。假定有$n_c$个有序属性、$n-n_c$个无序属性,不失一般性,令有序属性排列在无序属性之前,则:
\[MinkovDM_p(\mathbf{x_i},\mathbf{x_j}) = \left( \sum^{n_c}_{u=1} \lvert x_{iu} - x_{ju} \rvert^p + \sum^n_{u=n_c + 1} VDM_p (x_{iu},x_{ju}) \right) ^{\frac{1}{p}} \tag{2}\]当样本空间中不同属性的重要性不同时,可使用“加权距离”(weighted distance)。以加权闵可夫斯基距离为例:
\[dist_{wmk}(\mathbf{x_i},\mathbf{x_j}) = (w_1 \cdot \lvert x_{i1}-x_{j1} \rvert^p + \cdots + w_n \cdot \lvert x_{in} - x_{jn} \rvert ^p)^{\frac{1}{p}} \tag{3}\]其中权重$w_i \geqslant 0 \ (i=1,2,…,n)$表征不同属性的重要性,通常$\sum^n_{i=1} w_i = 1$。
需注意的是,通常我们是基于某种形式的距离来定义“相似度度量”,距离越大,相似度越小。然而,用于相似度度量的距离未必一定要满足距离度量的所有基本性质,尤其是直递性。例如:
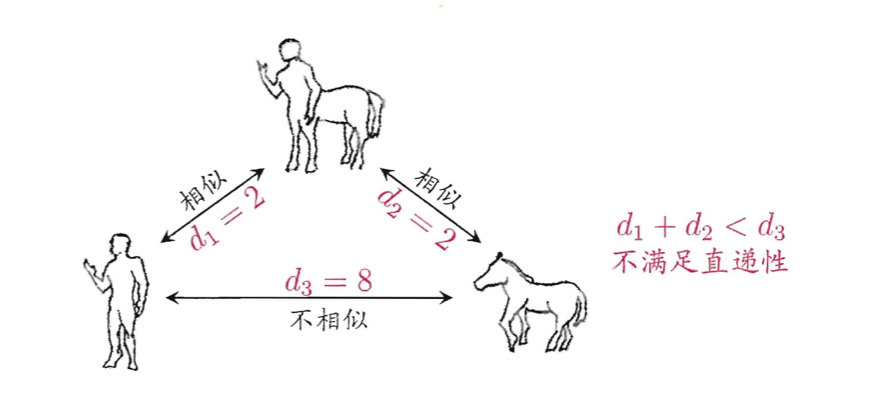
这个例子中,从数学上看,令$d_3=3$即可满足直递性;但从语义上看,$d_3$应远大于$d_1$与$d_2$。
此时该距离不再满足直递性;这样的距离称为“非度量距离”(non-metric distance)。此外,本文介绍的距离计算式都是事先定义好的,但在不少现实任务中,有必要基于数据样本来确定合适的距离计算式,这可通过“距离度量学习”(distance metric learning)来实现。