【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.原型聚类
“原型”是指样本空间中具有代表性的点。
原型聚类亦称“基于原型的聚类”(prototype-based clustering),此类算法假设聚类结构能通过一组原型刻画,在现实聚类任务中极为常用。接下来介绍几种著名的原型聚类算法。
2.k均值算法
给定样本集$D=\{\mathbf{x}_1,\mathbf{x}_2, … , \mathbf{x}_m \}$,“k均值”(k-means)算法针对聚类所得簇划分$\mathcal{C} = \{ C_1, C_2, … ,C_k \}$最小化平方误差:
\[E=\sum^k_{i=1} \sum_{\mathbf{x} \in C_i} \parallel \mathbf{x} - \mathbf{\mu}_i \parallel_2^2 \tag{1}\]其中$\mathbf{\mu}_i = \frac{1}{\lvert C_i \rvert} \sum_{\mathbf{x} \in C_i} \mathbf{x}$是簇$C_i$的均值向量。直观来看,式(1)在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,E值越小则簇内样本相似度越高。
最小化式(1)并不容易,找到它的最优解需考察样本集$D$所有可能的簇划分,这是一个NP难问题。因此,k均值算法采用了贪心策略,通过迭代优化来近似求解式(1)。算法流程如下图所示,其中第1行对均值向量进行初始化,在第4-8行与第9-16行依次对当前簇划分及均值向量迭代更新,若迭代更新后聚类结果保持不变,则在第18行将当前簇划分结果返回。

为避免运行时间过长,通过设置一个最大运行轮数或最小调整幅度阈值,若达到最大轮数或调整幅度小于阈值,则停止运行。
以下面的数据集为例演示k均值算法的学习过程。为方便叙述,我们将编号为$i$的样本称为$\mathbf{x}_i$,这是一个包含“密度”与“含糖率”两个属性值的二维向量:
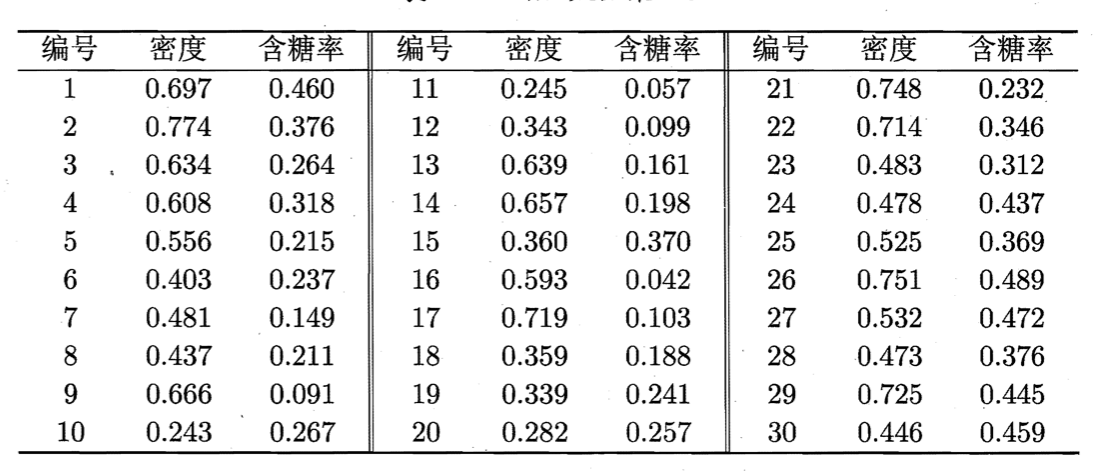
样本9~21的类别是“好瓜=否”,其他样本的类别是“好瓜=是”。由于本文使用无标记样本,因此类别标记信息未在表中给出。
假定聚类簇数$k=3$,算法开始时随机选取三个样本$\mathbf{x}_6,\mathbf{x}_{12},\mathbf{x}_{27}$作为初始均值向量,即:
\[\mathbf{\mu}_1=(0.403;0.237 ), \mathbf{\mu}_2=(0.343;0.099),\mathbf{\mu}_3=(0.532;0.472)\]对数据集中的所有样本考察一遍后,可得当前簇划分为:
\[C_1=\{\mathbf{x}_5,\mathbf{x}_6,\mathbf{x}_7,\mathbf{x}_8,\mathbf{x}_9,\mathbf{x}_{10},\mathbf{x}_{13},\mathbf{x}_{14},\mathbf{x}_{15},\mathbf{x}_{17},\mathbf{x}_{18},\mathbf{x}_{19},\mathbf{x}_{20},\mathbf{x}_{23} \}\] \[C_2=\{\mathbf{x}_{11},\mathbf{x}_{12},\mathbf{x}_{16} \}\] \[C_3 = \{\mathbf{x}_1,\mathbf{x}_2,\mathbf{x}_3,\mathbf{x}_4,\mathbf{x}_{21},\mathbf{x}_{22},\mathbf{x}_{24},\mathbf{x}_{25},\mathbf{x}_{26},\mathbf{x}_{27},\mathbf{x}_{28},\mathbf{x}_{29},\mathbf{x}_{30} \}\]于是,可从$C_1$、$C_2$、$C_3$分别求出新的均值向量:
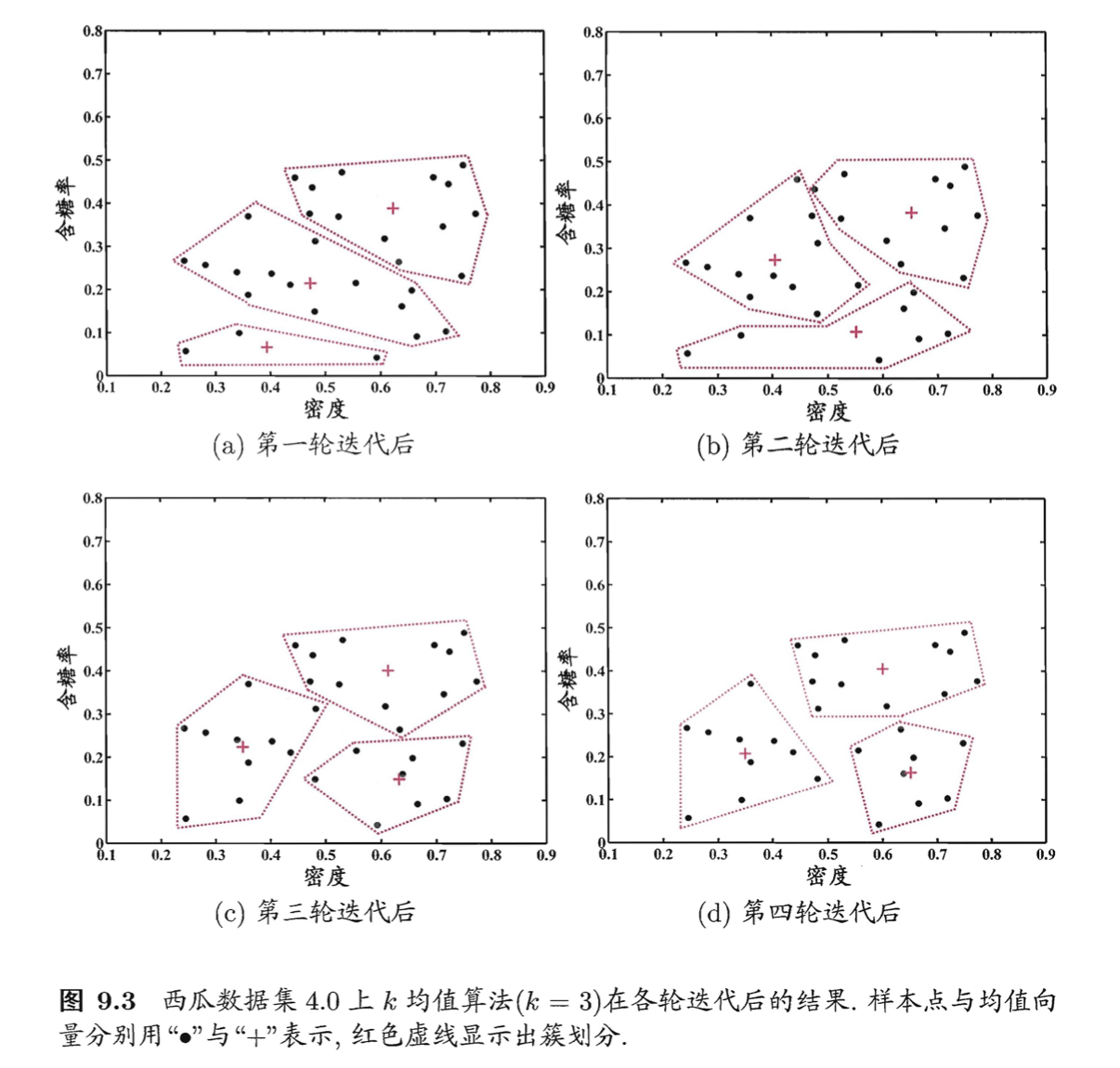
\[\mathbf{\mu}'_1=(0.473;0.214),\mathbf{\mu}'_2=(0.394;0.066),\mathbf{\mu}'_3=(0.623;0.388)\]更新当前均值向量后,不断重复上述过程,如下图所示,第五轮迭代产生的结果与第四轮迭代相同,于是算法停止,得到最终的簇划分:
3.学习向量量化
与k均值算法类似,“学习向量量化”(Learning Vector Quantization,简称LVQ)也是试图找到一组原型向量来刻画聚类结构,但与一般聚类算法不同的是,LVQ假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。
个人理解:LVQ属于是有监督的聚类方法。可用于将类别拆分为子类。
给定样本集$D=\{ (\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_m,y_m) \}$,每个样本$\mathbf{x}_j$是由$n$个属性描述的特征向量$(x_{j1};x_{j2};…;x_{jn}),y_j \in \mathcal{Y}$是样本$\mathbf{x}_j$的类别标记。LVQ的目标是学得一组$n$维原型向量$\{\mathbf{p}_1,\mathbf{p}_2,…,\mathbf{p}_q \}$,每个原型向量代表一个聚类簇,簇标记$t_i \in \mathcal{Y}$。

LVQ算法描述如上图所示,算法第1行先对原型向量进行初始化,例如对第$q$个簇可从类别标记为$t_q$的样本中随机选取一个作为原型向量。算法第2~12行对原型向量进行迭代优化。在每一轮迭代中,算法随机选取一个有标记训练样本,找出与其距离最近的原型向量,并根据两者的类别标记是否一致来对原型向量进行相应的更新。在第12行中,若算法的停止条件已满足(例如已达到最大迭代轮数,或原型向量更新很小甚至不再更新),则将当前原型向量作为最终结果返回。
显然,LVQ的关键是第6-10行,即如何更新原型向量。直观上看,对样本$\mathbf{x}_j$,若最近的原型向量$\mathbf{p}_{i^*}$与$\mathbf{x}_j$的类别标记相同,则令$\mathbf{p}_{i^*}$向$\mathbf{x}_j$的方向靠拢,如第7行所示,此时新原型向量为:
\[\mathbf{p}' = \mathbf{p}_{i^*}+\eta \cdot (\mathbf{x}_j - \mathbf{p}_{i^*}) \tag{2}\]$\mathbf{p}’$与$\mathbf{x}_j$之间的距离为:
\[\begin{align} \parallel \mathbf{p}' - \mathbf{x}_j \parallel_2 &= \parallel \mathbf{p}_{i^*}+\eta \cdot (\mathbf{x}_j - \mathbf{p}_{i^*}) - \mathbf{x}_j \parallel_2 \\&= (1-\eta) \cdot \parallel \mathbf{p}_{i^*} - \mathbf{x}_j \parallel _2 \end{align} \tag{3}\]令学习率$\eta \in (0,1)$,则原型向量$\mathbf{p}_{i^*}$在更新为$\mathbf{p}’$之后将更接近$\mathbf{x}_j$。
类似的,若$\mathbf{p}_{i^*}$与$\mathbf{x}_j$的类别标记不同,则更新后的原型向量与$\mathbf{x}_j$之间的距离将增大为$(1+\eta) \cdot \parallel \mathbf{p}_{i^*} - \mathbf{x}_j \parallel _2 $,从而更远离$\mathbf{x}_j$。
在学得一组原型向量$\{\mathbf{p}_1,\mathbf{p}_2,…,\mathbf{p}_q \}$后,即可实现对样本空间$\chi$的簇划分。对任意样本$\mathbf{x}$,它将被划入与其距离最近的原型向量所代表的簇中;换言之,每个原型向量$\mathbf{p}_i$定义了与之相关的一个区域$R_i$,该区域中每个样本与$\mathbf{p}_i$的距离不大于它与其他原型向量$\mathbf{p}_{i’}(i’ \neq i)$的距离,即:
\[R_i = \{ \mathbf{x} \in \chi \mid \parallel \mathbf{x}-\mathbf{p}_i \parallel_2 \leqslant \parallel \mathbf{x} - \mathbf{p}_{i'} \parallel_2, i' \neq i \} \tag{4}\]由此形成了对样本空间$\chi$的簇划分$\{R_1,R_2,…,R_q \}$,该划分通常称为“Voronoi剖分”(Voronoi tessellation)。
若将$R_i$中样本全用原型向量$\mathbf{p}_i$表示,则可实现数据的“有损压缩”(lossy compression),这称为“向量量化”(vector quantization);LVQ由此而得名。
个人理解:所以LVQ也可用于数据的有损压缩。
我们依旧以第2部分的数据集为例来演示LVQ的学习过程。令9-21号样本的类别标记为$c_2$,其他样本的类别标记为$c_1$。假定$q=5$,即学习目标是找到5个原型向量$\mathbf{p}_1,\mathbf{p}_2,\mathbf{p}_3,\mathbf{p}_4,\mathbf{p}_5$,并假定其对应的类别标记分别为$c_1,c_2,c_2,c_1,c_1$。
即希望为“好瓜=是”找到3个簇,“好瓜=否”找到2个簇。
算法开始时,根据样本的类别标记和簇的预设类别标记对原型向量进行随机初始化,假定初始化为样本$\mathbf{x}_5,\mathbf{x}_{12},\mathbf{x}_{18},\mathbf{x}_{23},\mathbf{x}_{29}$。在第一轮迭代中,假定随机选取的样本为$\mathbf{x}_1$,该样本与当前原型向量$\mathbf{p}_1,\mathbf{p}_2,\mathbf{p}_3,\mathbf{p}_4,\mathbf{p}_5$的距离分别为$0.283,0.506,0.434,0.260,0.032$。由于$\mathbf{p}_5$与$\mathbf{x}_1$距离最近且两者具有相同的类别标记$c_2$,假定学习率$\eta=0.1$,则LVQ更新$\mathbf{p}_5$得到新原型向量:
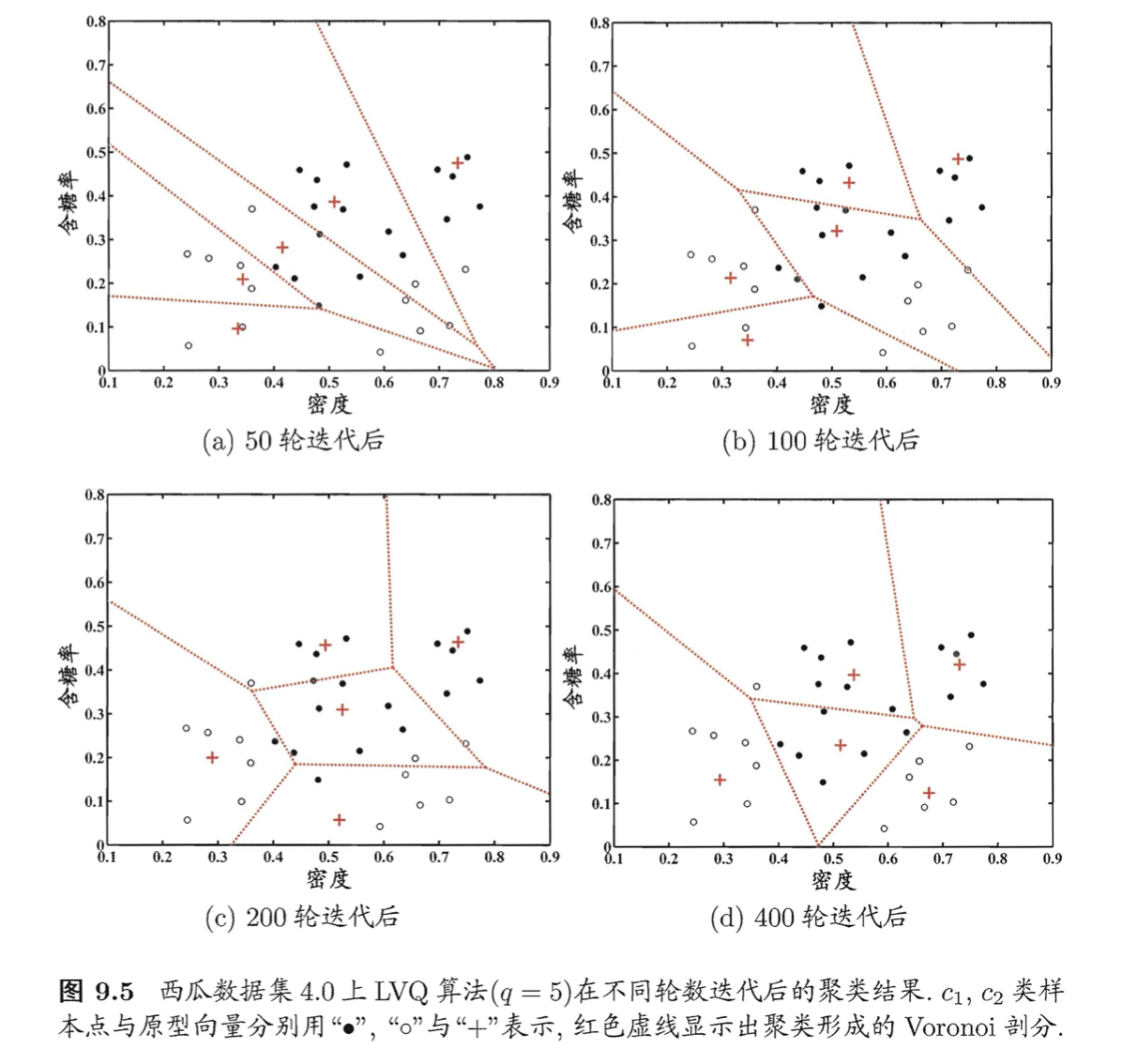
\[\begin{align} \mathbf{p}' &= \mathbf{p}_5 + \eta \cdot (\mathbf{x}_1 - \mathbf{p}_5) \\&= (0.725;0.445) + 0.1 \cdot ((0.697;0.460)-(0.725;0.445)) \\&= (0.722;0.442) \end{align}\]将$\mathbf{p}_5$更新为$\mathbf{p}’$后,不断重复上述过程,不同轮数之后的聚类结果见下图:
4.高斯混合聚类
与k均值、LVQ用原型向量来刻画聚类结构不同,高斯混合聚类采用概率模型来表达聚类原型。
我们先简单回顾一下(多元)高斯分布的定义。对$n$维样本空间$\chi$中的随机向量$\mathbf{x}$,若$\mathbf{x}$服从高斯分布,其概率密度函数为:
\[p(\mathbf{x})=\frac{1}{(2\pi)^{\frac{n}{2}} \lvert \Sigma \rvert ^{\frac{1}{2}}} e^{-\frac{1}{2} (\mathbf{x} - \mathbf{\mu})^T \Sigma^{-1} (\mathbf{x} - \mathbf{\mu})} \tag{5}\]记为$\mathbf{x} \sim \mathcal{N}(\mathbf{\mu},\Sigma)$。
$\Sigma$:对称正定矩阵。
$\lvert \Sigma \rvert$:$\Sigma$的行列式。
$\Sigma^{-1}$:$\Sigma$的逆矩阵。
其中$\mathbf{\mu}$是$n$维均值向量,$\Sigma$是$n\times n$的协方差矩阵。由式(5)可看出,高斯分布完全由均值向量$\mathbf{\mu}$和协方差矩阵$\Sigma$这两个参数确定。为了明确显示高斯分布与相应参数的依赖关系,将概率密度函数记为$p(\mathbf{x} \mid \mathbf{\mu},\Sigma)$。
我们可定义高斯混合分布:
\[p_{\mathcal{M}}(\mathbf{x})=\sum^k_{i=1}\alpha_i \cdot p(\mathbf{x} \mid \mathbf{\mu}_i,\Sigma_i) \tag{6}\]$p_{\mathcal{M}}(\cdot)$也是概率密度函数,$\int p_{\mathcal{M}}(\mathbf{x})d\mathbf{x}=1$。
该分布共由$k$个混合成分组成,每个混合成分对应一个高斯分布。其中$\mathbf{\mu}_i$与$\Sigma_i$是第$i$个高斯混合成分的参数,而$\alpha_i>0$为相应的“混合系数”,$\sum^k_{i=1} \alpha_i=1$。
假设训练集$D=\{ \mathbf{x}_1,\mathbf{x}_2,…,\mathbf{x}_m \}$,令随机变量$z_j \in \{1,2,…,k \}$表示样本$\mathbf{x}_j$的高斯混合成分,其取值未知。显然,$z_j$的先验概率$P(z_j=i)$对应于$\alpha_i(i=1,2,…,k)$。根据贝叶斯定理,$z_j$的后验分布对应于:
\[\begin{align} p_{\mathcal{M}}(z_j =i \mid \mathbf{x}_j) &= \frac{P(z_j=i) \cdot p_{\mathcal{M}}(\mathbf{x}_j \mid z_j = i)}{p_{\mathcal{M}}(\mathbf{x}_j)} \\&= \frac{\alpha_i \cdot p(\mathbf{x}_j \mid \mathbf{\mu}_i,\Sigma_i) }{\sum^k_{l=1} \alpha_l \cdot p( \mathbf{x}_j \mid \mathbf{\mu}_l,\Sigma_l ) } \end{align} \tag{7}\]换言之,$p_{\mathcal{M}}(z_j=i \mid \mathbf{x}_j)$给出了样本$\mathbf{x}_j$由第$i$个高斯混合成分生成的后验概率。为方便叙述,将其简记为$\gamma_{ji}(i=1,2,…,k)$。
当高斯混合分布(6)已知时,高斯混合聚类将把样本集$D$划分为$k$个簇$\mathcal{C}=\{C_1,C_2,…,C_k \}$,每个样本$\mathbf{x}_j$的簇标记$\lambda_j$如下确定:
\[\lambda_j = \mathop{\arg \max} \limits_{i \in \{1,2,...,k \}} \gamma_{ji} \tag{8}\]因此,从原型聚类的角度来看,高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画,簇划分则由原型对应后验概率确定。
那么,对于式(6),模型参数$\{(\alpha_i,\mathbf{\mu}_i,\Sigma_i) \mid 1 \leqslant i \leqslant k \}$如何求解呢?显然,给定样本集$D$,可采用极大似然估计,即最大化(对数)似然:
\[\begin{align} LL(D) &= \ln \left( \prod^m_{j=1} p_{\mathcal{M}}(\mathbf{x}_j) \right) \\&= \sum^m_{j=1} \ln \left( \sum^k_{i=1} \alpha_i \cdot p(\mathbf{x}_j \mid \mathbf{\mu}_i,\Sigma_i ) \right) \end{align} \tag{9}\]常采用EM算法进行迭代优化求解。下面我们做一个简单的推导。
若参数$\{(\alpha_i,\mathbf{\mu}_i,\Sigma_i) \mid 1 \leqslant i \leqslant k \}$能使式(9)最大化,则由$\frac{\partial LL(D)}{\partial \mathbf{\mu}_i}=0$有:
\[\mathbf{\mu}_i = \frac{\sum^m_{j=1} \gamma_{ji} \mathbf{x}_j}{\sum^m_{j=1} \gamma_{ji}} \tag{10}\]公式推导请见:南瓜书公式(9.34)的推导。
类似的,由$\frac{\partial LL(D)}{\partial \Sigma_i}=0$可得:
\[\Sigma_i = \frac{ \sum^m_{j=1} \gamma_{ji} (\mathbf{x}_j - \mathbf{\mu} _i) (\mathbf{x}_j - \mathbf{\mu} _i)^T }{\sum^m_{j=1} \gamma_{ji}} \tag{11}\]公式推导请见:南瓜书公式(9.35)的推导。
对于混合系数$\alpha_i$,除了要最大化$LL(D)$,还需满足$\alpha_i \geqslant 0, \sum^k_{i=1} \alpha_i = 1$。考虑$LL(D)$的拉格朗日形式:
\[LL(D)+\lambda\left( \sum^k_{i=1} \alpha_i - 1 \right) \tag{12}\]其中$\lambda$为拉格朗日乘子($\lambda=-m$)。由式(12)对$\alpha_i$的导数为0,有:
\[\alpha_i = \frac{1}{m} \sum^m_{j=1} \gamma_{ji} \tag{13}\]公式推导请见:南瓜书公式(9.38)的推导。

式(9.30)为式(7)。
式(9.31)为式(8)。
EM算法停止条件可以是已达到最大迭代轮数,或似然函数$LL(D)$增长很少甚至不再增长。
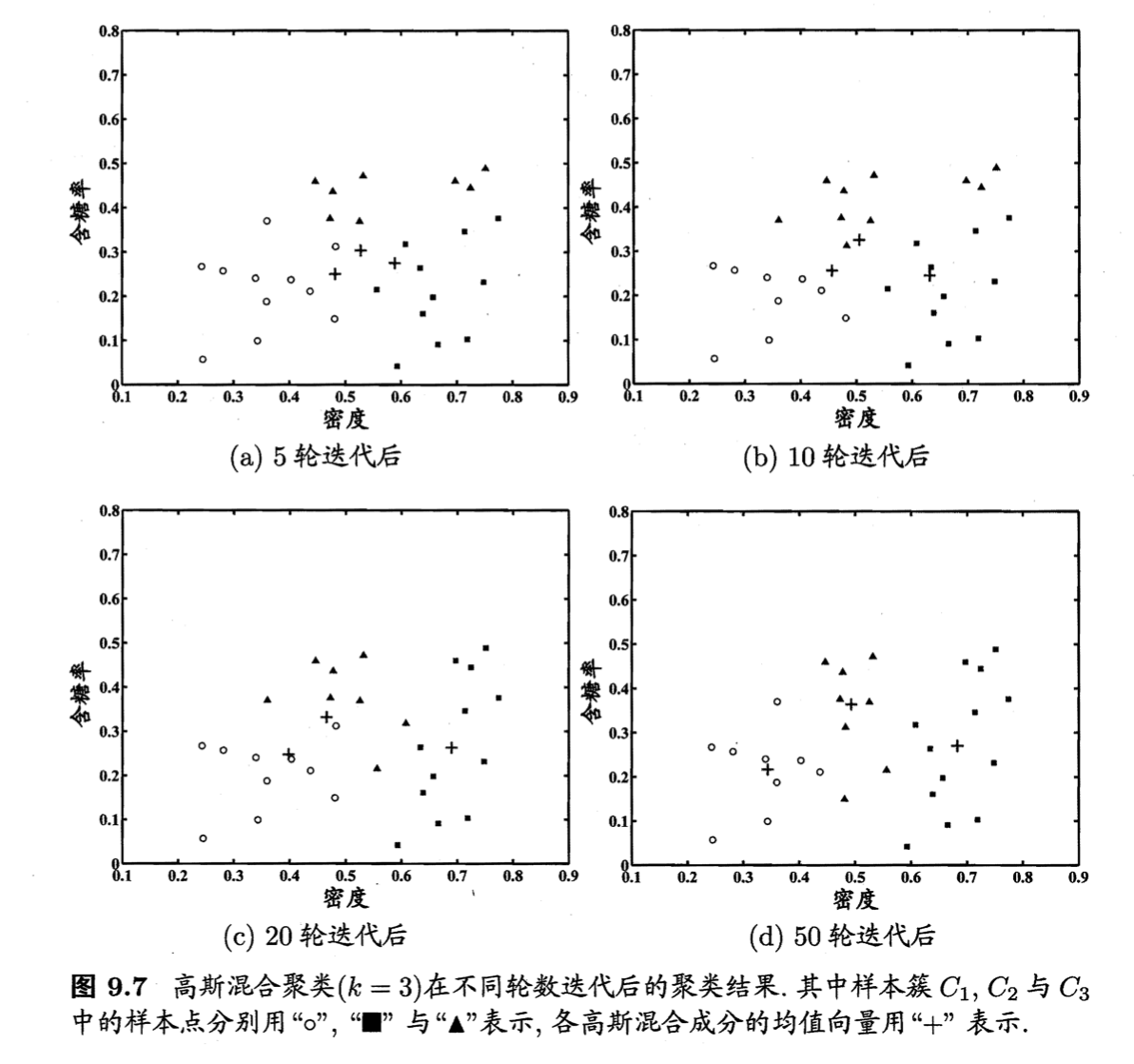
高斯混合聚类算法描述见上图。以第2部分的数据集为例,令高斯混合成分的个数$k=3$。算法开始时,假定将高斯混合分布的模型参数初始化为:
\[\alpha_1 = \alpha_2 = \alpha_3 = \frac{1}{3}\] \[\mathbf{\mu}_1 = \mathbf{x}_6, \mathbf{\mu}_2 = \mathbf{x}_{22}, \mathbf{\mu}_3 = \mathbf{x}_{27}\] \[\Sigma_1=\Sigma_2=\Sigma_3=\begin{pmatrix} 0.1 & 0.0 \\ 0.0 & 0.1 \\ \end{pmatrix}\]在第一轮迭代中,先计算样本由各混合成分生成的后验概率。以$\mathbf{x}_1$为例,由式(7)算出后验概率$\gamma_{11}=0.219,\gamma_{12}=0.404,\gamma_{13}=0.377$。所有样本的后验概率算完后,得到如下新的模型参数:
\[\alpha_1'=0.361,\alpha_2'=0.323,\alpha_3'=0.316\] \[\mathbf{\mu}_1'=(0.491;0.251), \mathbf{\mu}_2'=(0.571;0.281),\mathbf{\mu}_3'=(0.534;0.295)\] \[\Sigma_1'=\begin{pmatrix} 0.025 & 0.004 \\ 0.004 & 0.016 \\ \end{pmatrix}, \Sigma_2'=\begin{pmatrix} 0.023 & 0.004 \\ 0.004 & 0.017 \\ \end{pmatrix}, \Sigma_3' = \begin{pmatrix} 0.024 & 0.005 \\ 0.005 & 0.016 \\ \end{pmatrix}\]模型参数更新后,不断重复上述过程,不同轮数之后的聚类结果见下: