本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.ABSTRACT
本博文只介绍原文的部分章节,原文链接在本文末尾。
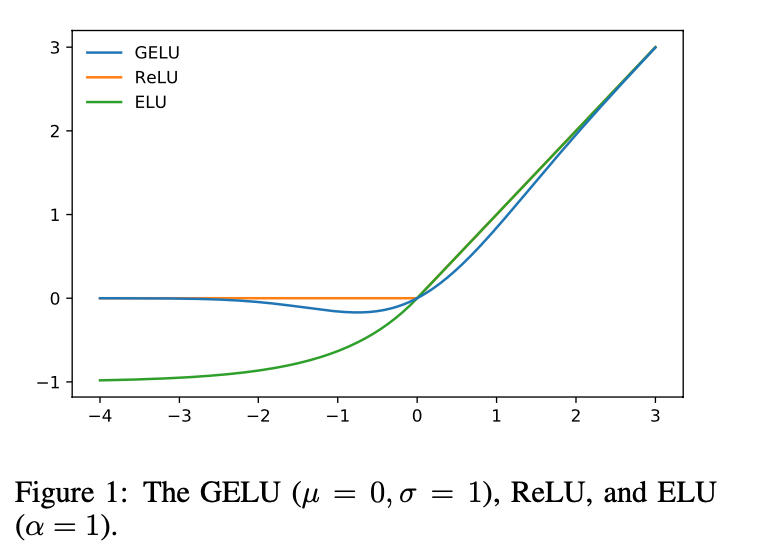
我们提出Gaussian Error Linear Unit(GELU),一种高性能的神经网络激活函数。GELU可表示为$x\Phi (x)$,其中$\Phi (x)$为标准高斯累积分布函数(即概率分布函数)。我们将GELU和ReLU、ELU进行了对比,结果发现我们的方法在CV、NLP、speech task等方面都优于ReLU和ELU。
2.GELU FORMULATION
zoneout是用于RNN的一种正则化方法,原文:David Krueger, Tegan Maharaj, Jnos Krama ́r, Mohammad Pezeshki, Nicolas Ballas, Nan Rosemary Ke1, Anirudh Goyal, Yoshua Bengio, Hugo Larochelle, Aaron Courville, and Chris Pal. Zoneout: Regularizing RNNs by randomly preserving hidden activations. In Neural Information Processing Systems, 2016.。
GELU的定义为:
\[\text{GELU} (x) = x P(X \leqslant x) = x \Phi (x) = x \frac{1}{2} \left[ 1+\text{erf} (x/ \sqrt{2}) \right]\]误差函数(error function,简称erf)定义为:
$\text{erf} (x)=\frac{1}{\sqrt{\pi}} \int^x_{-x} e^{-t^2} dt=\frac{2}{\sqrt{\pi}} \int^x_0 e^{-t^2} dt$
GELU可近似计算为:
\[0.5x(1+ \tanh [ \sqrt{2/\pi} (x+0.044715x^3) ])\]或:
\[x\sigma (1.702x)\]近似计算的好处就是牺牲一定的精度换取更快的计算速度。
我们可以使用不同的CDF(即上式中的$\sigma(\cdot)$函数)。例如,我们可以将CDF $\sigma(x)$定义为Logistic Distribution,此时我们将其称为Sigmoid Linear Unit(SiLU):$x\sigma (x)$。此外,我们也可以将CDF定义为正态分布$\mathcal{N} (\mu,\sigma^2)$,此时$\mu,\sigma$为可学习的超参数,在我们的实验中使用$\mu=0,\sigma=1$。
3.GELU EXPERIMENTS
- MNIST classification(灰度图像,10个类别,60k训练集,10k测试集)。
- MNIST autoencoding。
- Tweet part-of-speech tagging(训练集1000个样本,验证集327个样本,测试集500个样本)。
- TIMIT frame recognition(训练集3696个样本,验证集1152个样本,测试集192个样本)。
- CIFAR-10/100 classification(彩色图像,10/100个类别,50k训练集,10k测试集)。
3.1.MNIST CLASSIFICATION
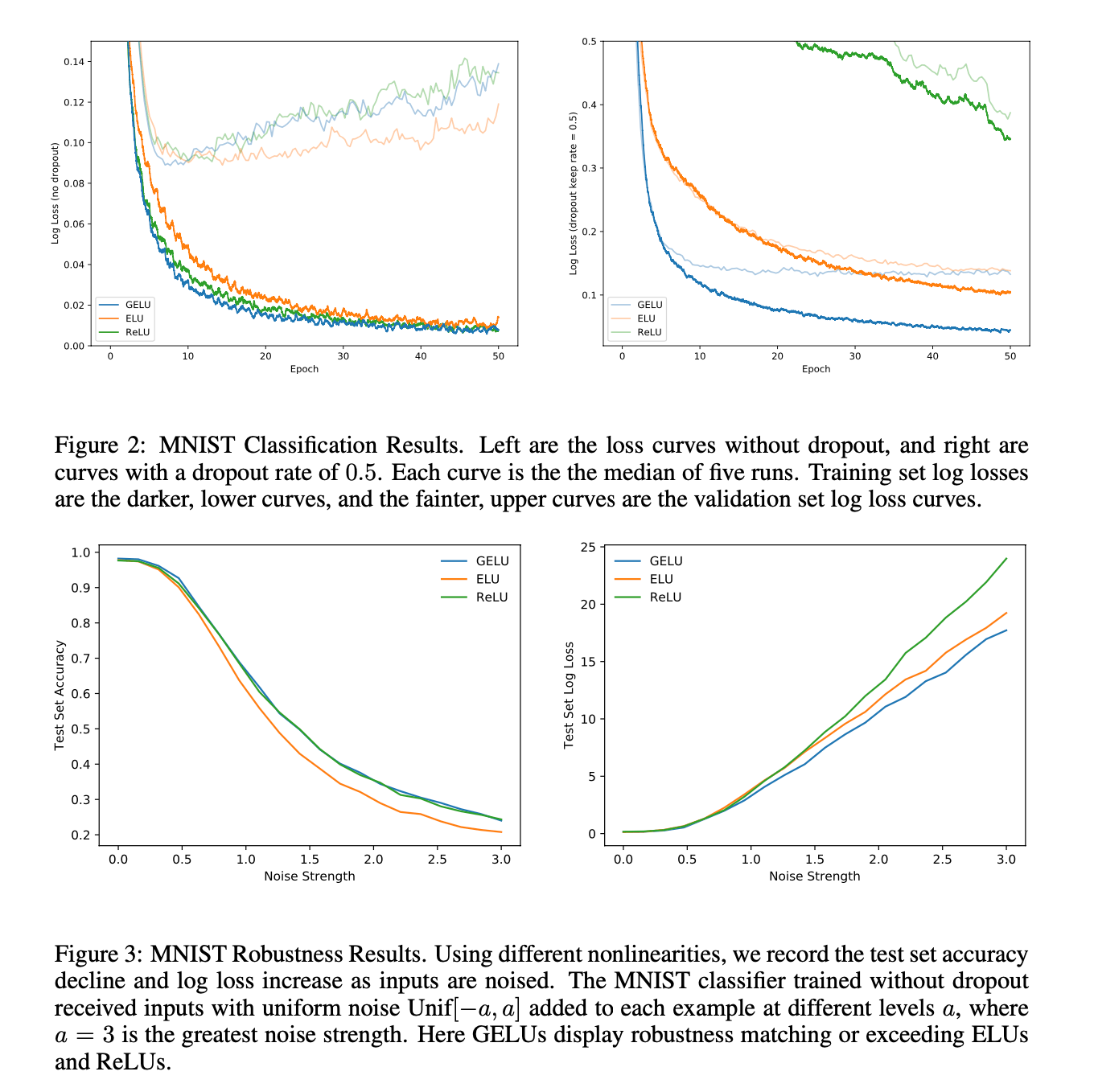
使用一个8层的全连接神经网络,每层128个神经元,训练50个epoch,mini-batch size=128,使用Adam优化算法。根据5k的验证集对学习率进行调整:$\{ 10^{-3},10^{-4},10^{-5} \}$,最终结果取5次(每一次对应一种权重初始化方式)运行结果的平均。Fig3显示了GELU对噪声的鲁棒性。Fig2展示了几种激活函数在使用或不使用dropout时的log loss的变化。
3.2.MNIST AUTOENCODER
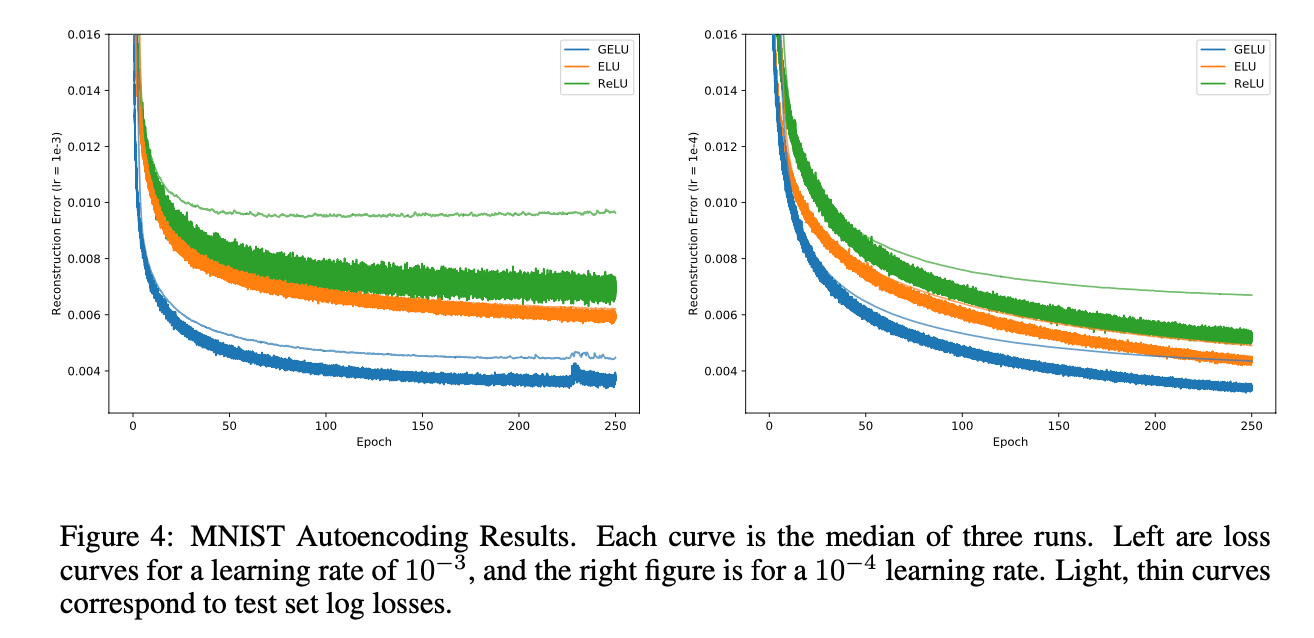
设置网络每层的神经元数为1000,500,250,30,250,500,1000。mini-batch size=64,使用Adam优化算法。loss使用均方误差。学习率从$10^{-3}$变化至$10^{-4}$。我们也尝试了学习率设为0.01,但是ELUs不收敛,GELUs和ReLUs收敛效果很差。对比结果见Fig4:
3.3.TWITTER POS TAGGING
NLP中的许多数据集都相对较小,所以用于NLP的激活函数也得能在小数据集上有不错的性能。在此任务上三种激活函数的test set error分别为:GELU(12.57%)、ReLU(12.67%)、ELU(12.91%)。
任务描述以及模型细节不再赘述,有需要的可以自行查看博文末尾的全文链接。
3.4.TIMIT FRAME CLASSIFICATION
对比结果见Fig5:
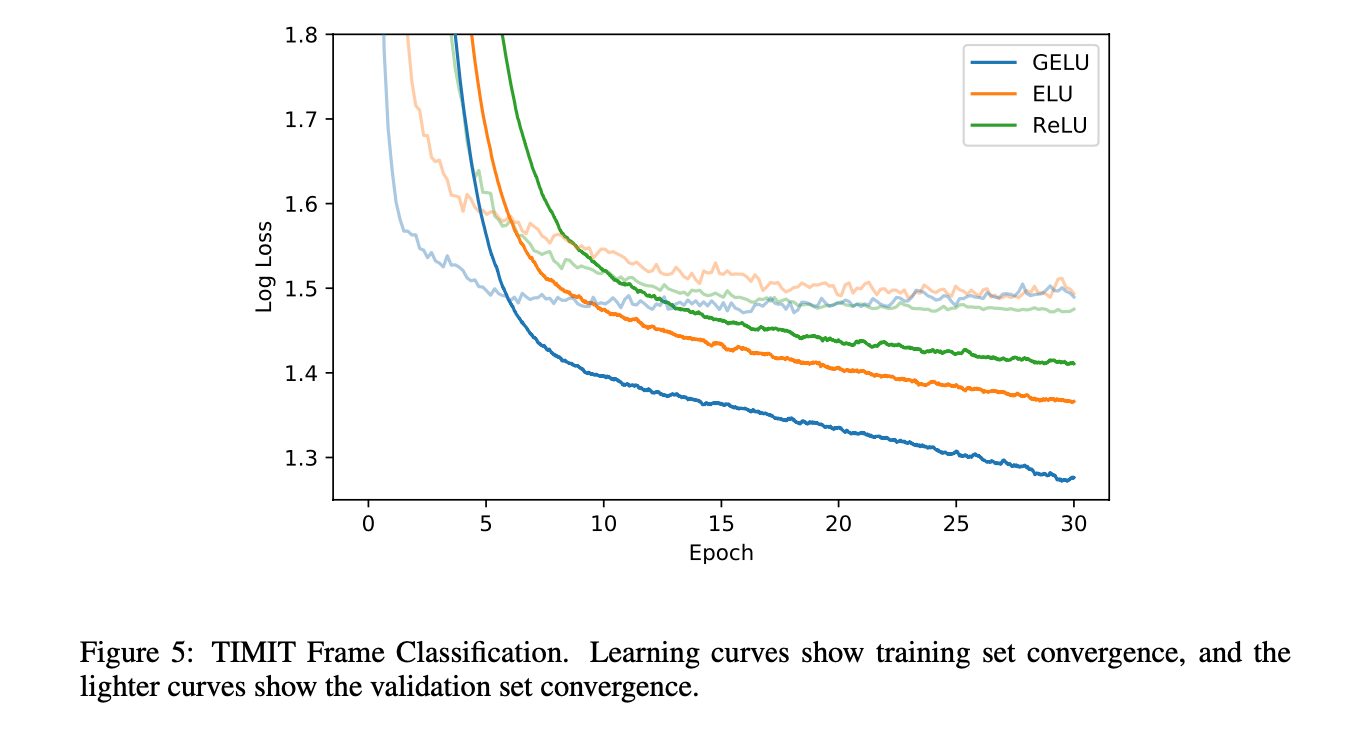
任务描述以及模型细节不再赘述,有需要的可以自行查看博文末尾的全文链接。
3.5.CIFAR-10/100 CLASSIFICATION
本小节我们将证明对于复杂的体系结构,GELU依然优于其他非线性激活函数。我们使用CIFAR-10/100数据集,模型使用浅的CNN。
在CIFAR-10数据集上,我们所用的CNN只有9层,使用了BatchNorm。模型结构见下:
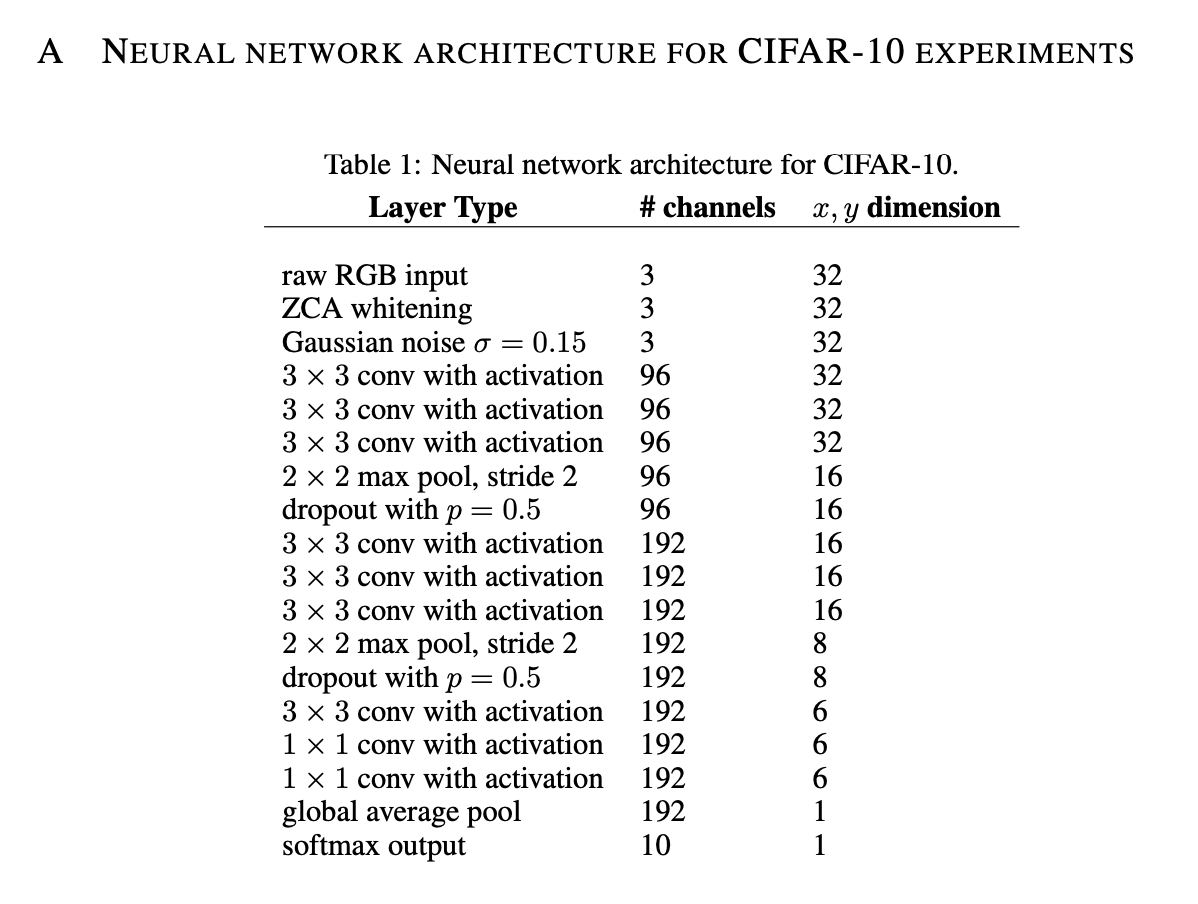
训练阶段没有使用data augmentation。学习率调整策略同第3.1部分。使用Adam优化算法,运行了200个epoch。结果见Fig6。最终,GELU的错误率为7.89%,ReLU的错误率为8.16%,ELU的错误率为8.41%。
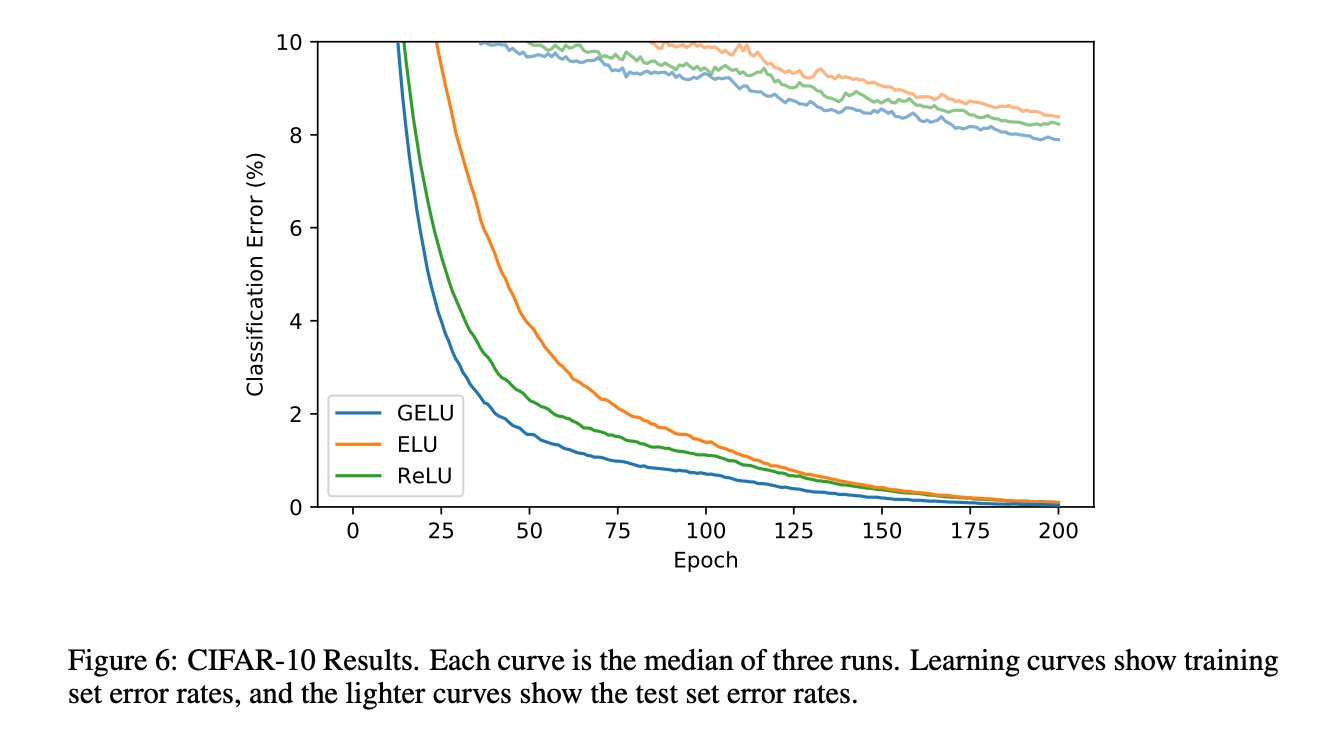
对于CIFAR-100数据集,我们使用一个40层的残差网络。模型结构及训练细节不再赘述,结果见Fig7。
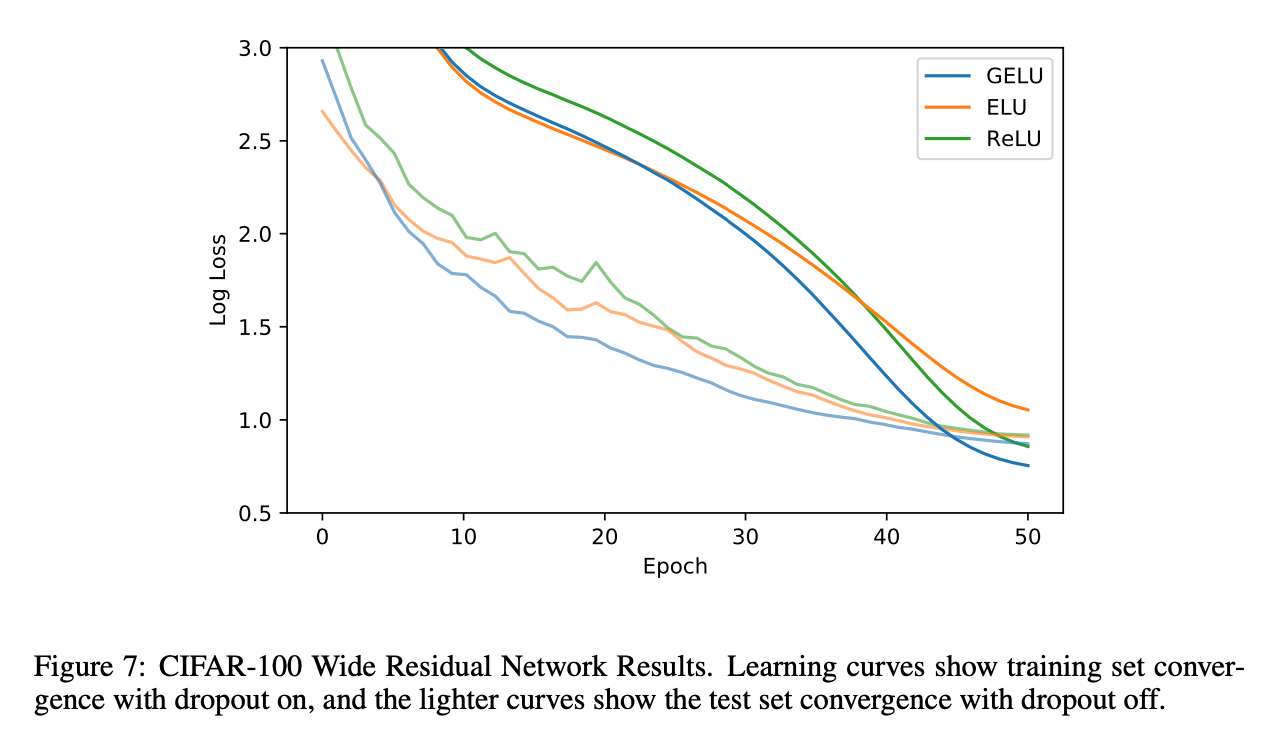
4.DISCUSSION
在之前的实验中,虽然GELU比ReLU和ELU都要优秀,但是其与ReLU和ELU在某些方面还是有一定相似性的。比如,当$\sigma \to 0 ,\mu=0$时,GELU就变成了ReLU。GELU和ReLU是一种渐进的关系。GELU可以看作是ReLU的平滑版本。
GELU是非凸、非单调函数,在正值部分是非线性的。而ReLU和ELU是单调凸函数,在正值部分是线性的。
对于使用GELU,我们有两个实用的tips:1)搭配带有momentum的优化算法;2)使用尽可能接近高斯分布的概率分布函数。比如,sigmoid function $\sigma(x)=1/(1+e^{-x})$就是正态分布的概率分布函数的近似。我们发现SiLU(即$x\sigma (x),\ \sigma(x)=1/(1+e^{-x})$)的表现不如GELU,但是仍优于ReLU和ELU,所以SiLU也是个不错的选择。