【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.层次聚类
层次聚类(hierarchical clustering)试图在不同层次对数据集进行划分,从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略,也可采用“自顶向下”的分拆策略。
AGNES(AGglomerative NESting)是一种采用自底向上聚合策略的层次聚类算法。它先将数据集中的每个样本看作一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直至达到预设的聚类簇个数。例如,给定聚类簇$C_i$与$C_j$,可通过下面的式子来计算距离:
\[最小距离:d_{min}(C_i,C_j)=\min \limits_{\mathbf{x} \in C_i, \mathbf{z}\in C_j} \text{dist}(\mathbf{x},\mathbf{z}) \tag{1}\] \[最大距离:d_{max}(C_i,C_j)=\max \limits_{\mathbf{x} \in C_i, \mathbf{z}\in C_j} \text{dist}(\mathbf{x},\mathbf{z}) \tag{2}\] \[平均距离:d_{avg}(C_i,C_j)=\frac{1}{\lvert C_i \rvert \lvert C_j \rvert} \sum_{\mathbf{x} \in C_i} \sum_{\mathbf{z}\in C_j} \text{dist}(\mathbf{x},\mathbf{z}) \tag{3}\]更多计算方式请见:链接。
显然,最小距离由两个簇的最近样本决定,最大距离由两个簇的最远样本决定,而平均距离则由两个簇的所有样本共同决定。当聚类簇距离由$d_{min}$、$d_{max}$或$d_{avg}$计算时,AGNES算法被相应地称为“单链接”(single-linkage)、“全链接”(complete-linkage)或“均链接”(average-linkage)算法。
AGNES算法描述如下图所示:

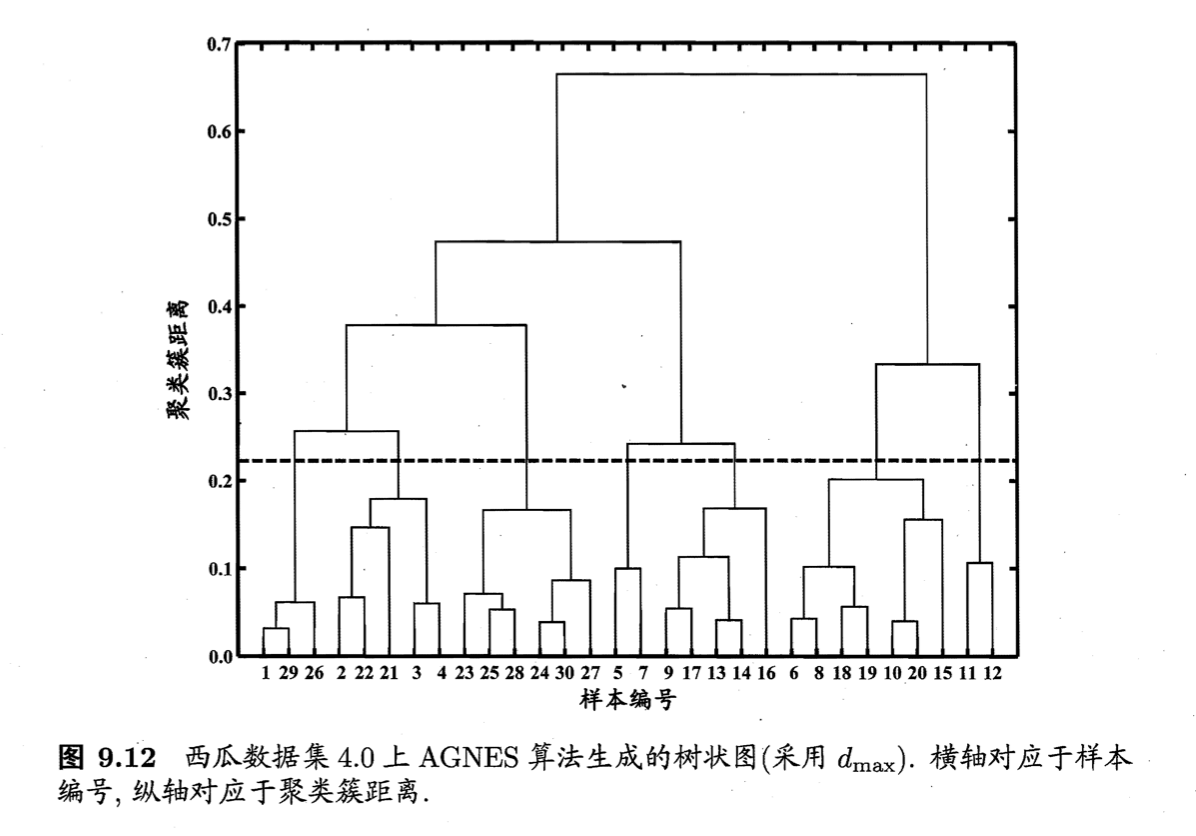
依旧以西瓜数据集为例,令AGNES算法一直执行到所有样本出现在同一个簇中,即$k=1$,则可得到下图所示的“树状图”(dendrogram),其中每层链接一组聚类簇。
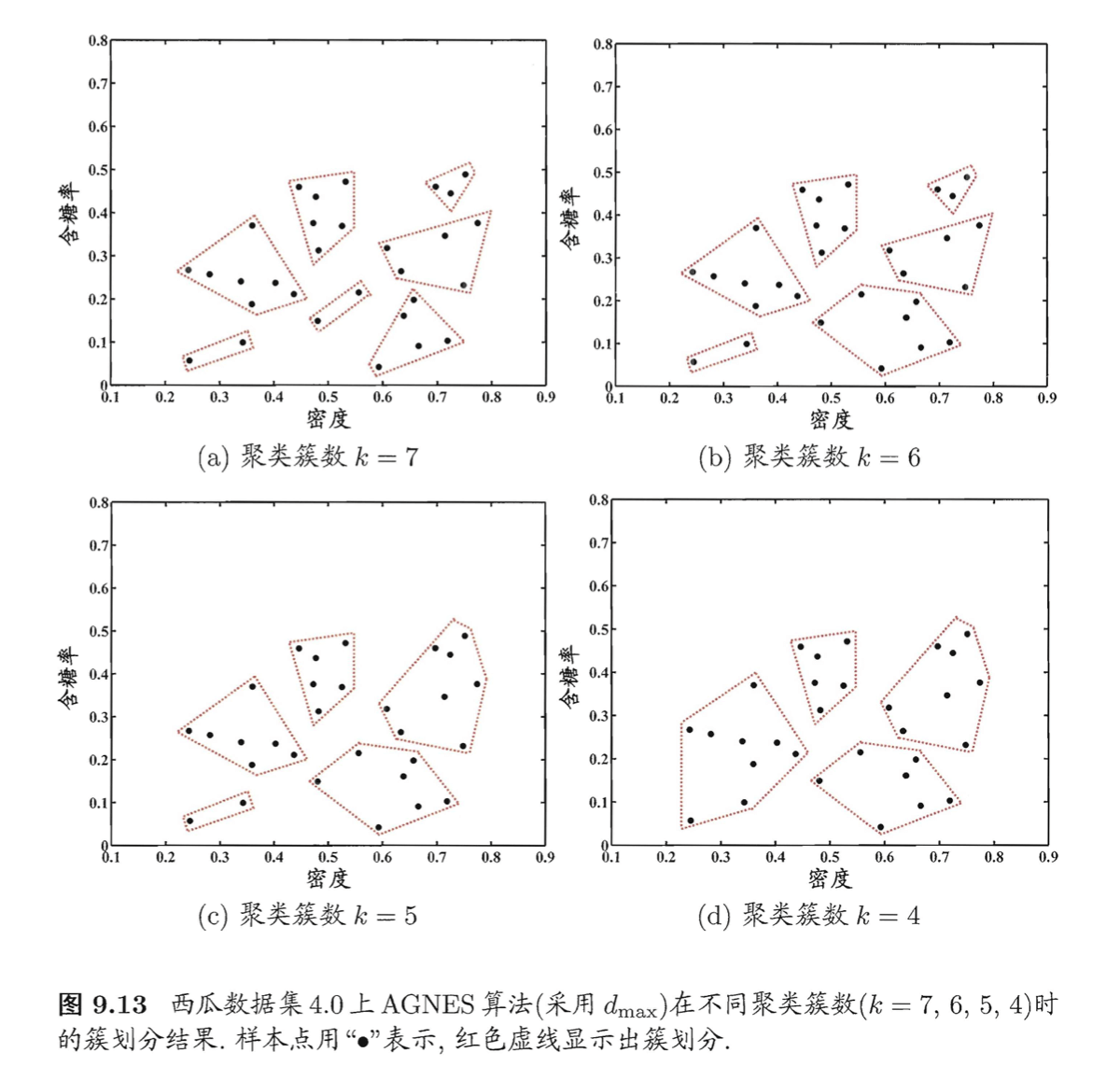
将分割层逐步提升,则可得到聚类簇逐渐减少的聚类结果: