本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.使用Python实现层次聚类
层次聚类的介绍请见:【机器学习基础】第三十七课:聚类之层次聚类。层次聚类有“Agglomerative”(bottom-up)和“Divisive”(top-down)两种方式:
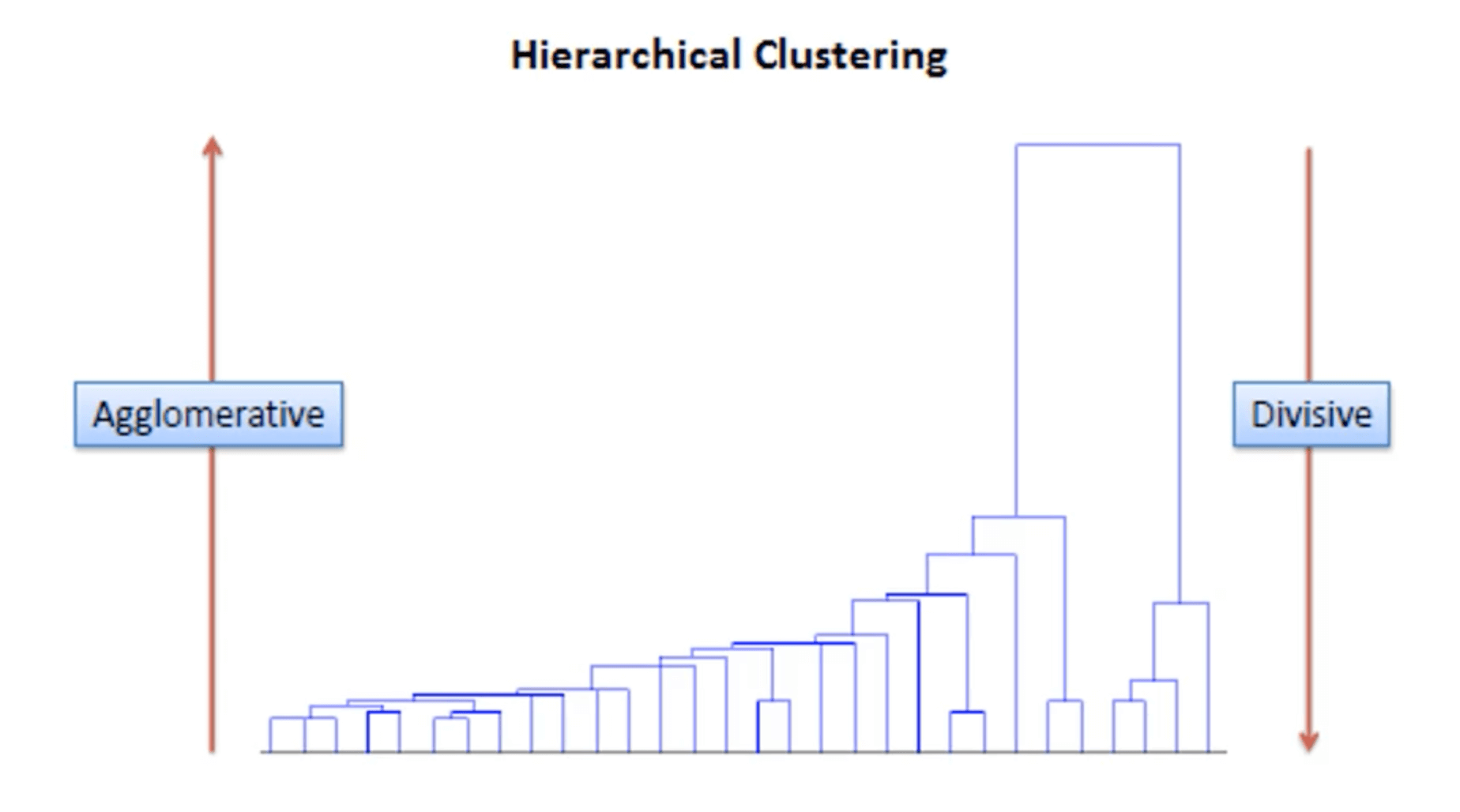
👉使用scipy绘制树状图:
1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.datasets import load_iris
iris = load_iris()
import scipy.cluster.hierarchy as sch
import matplotlib.pyplot as plt
dendrogram = sch.dendrogram(sch.linkage(iris.data, method='ward'))
plt.title('Dendrogram')
plt.xlabel('Iris')
plt.ylabel('Euclidean distances')
plt.show()
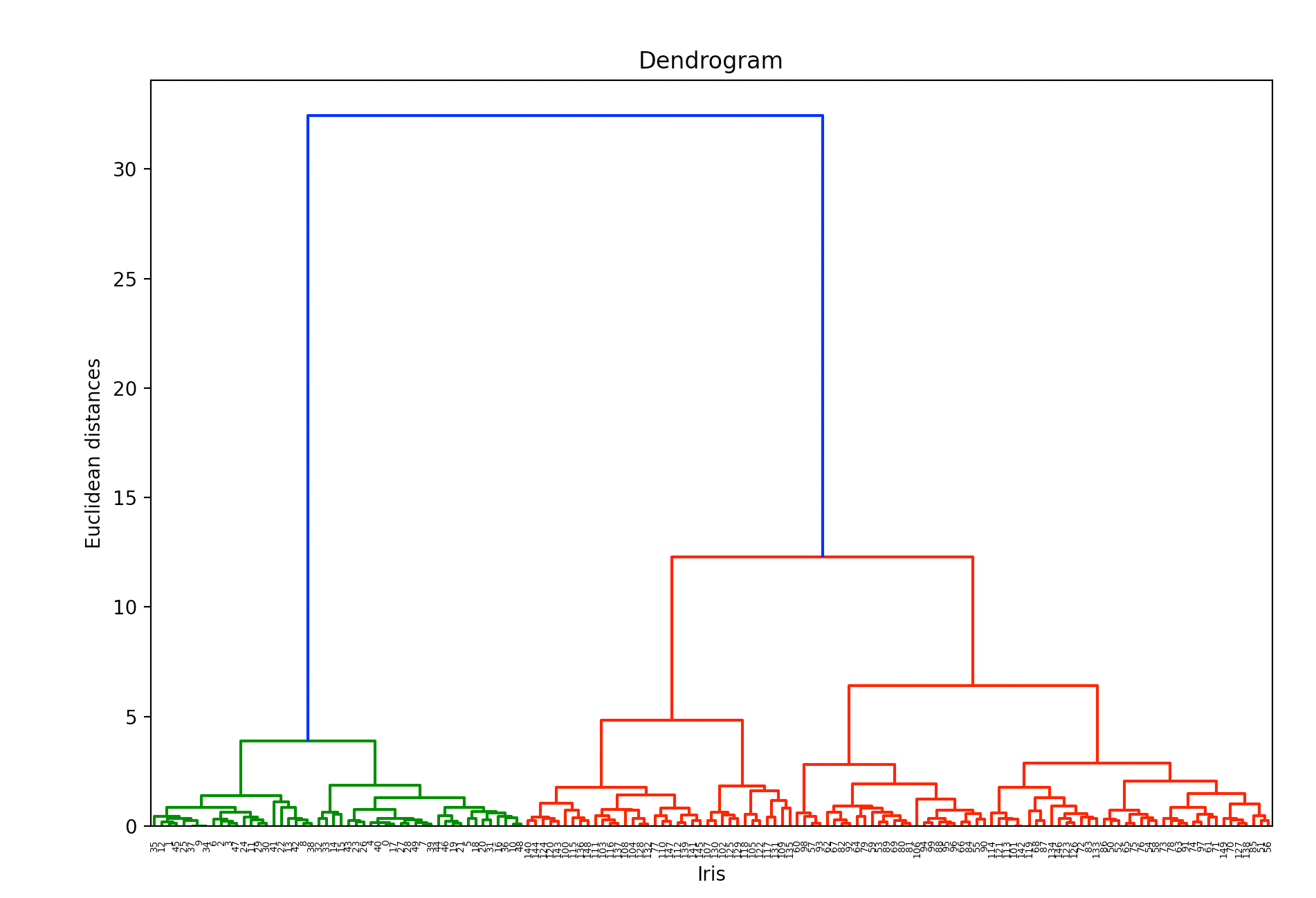
sch.linkage的讲解见本文第2部分。sch.dendrogram用于绘制树状图。
👉使用sklearn进行层次聚类(Agglomerative方式):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.cluster import AgglomerativeClustering
hc = AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='ward')
y_hc = hc.fit_predict(iris.data)
plt.scatter(iris.data[y_hc == 0, 2], iris.data[y_hc == 0, 3], s=100, c='red', label='Cluster1')
plt.scatter(iris.data[y_hc == 1, 2], iris.data[y_hc == 1, 3], s=100, c='blue', label='Cluster2')
plt.scatter(iris.data[y_hc == 2, 2], iris.data[y_hc == 2, 3], s=100, c='green', label='Cluster3')
plt.title('Clusters of Iris')
plt.xlabel('Petal.Length')
plt.ylabel('Petal.Width')
plt.legend()
plt.show()
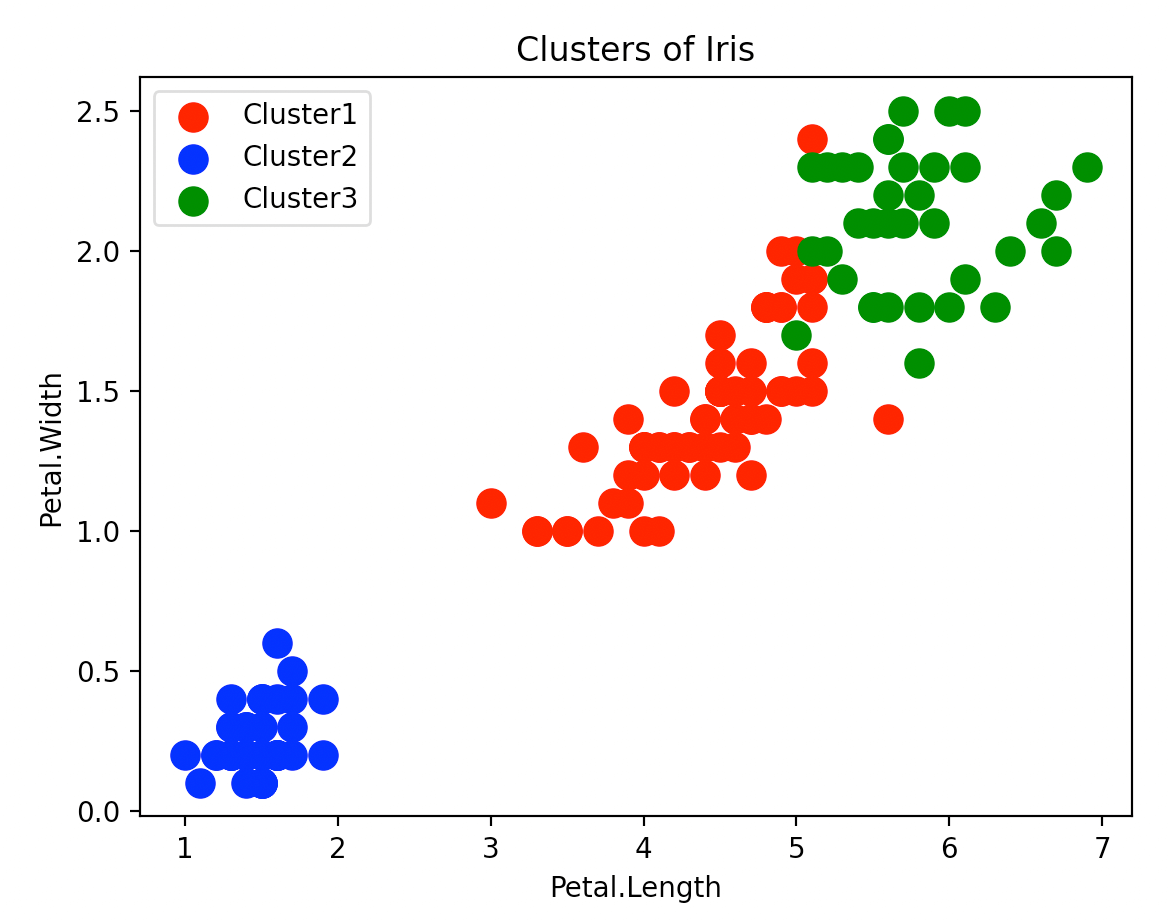
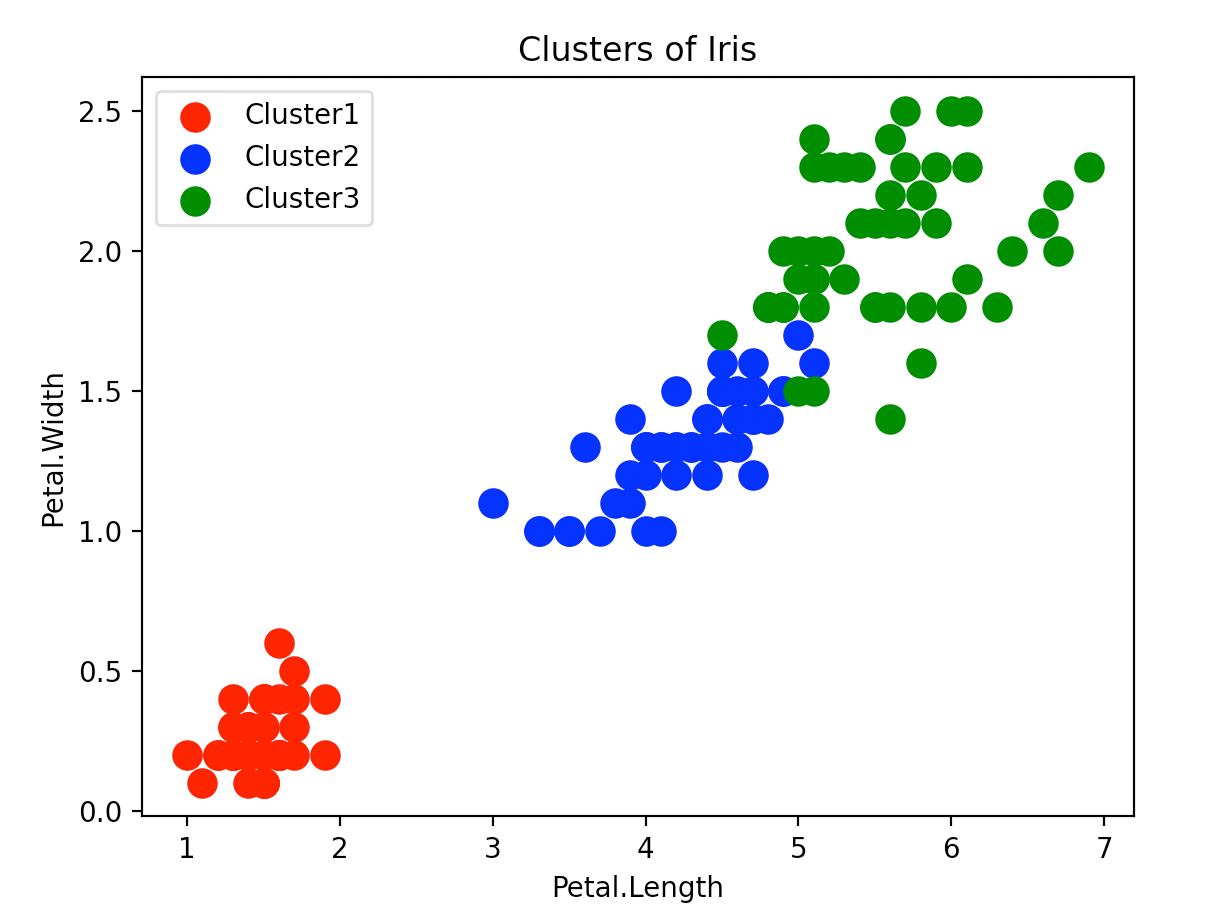
与真实结果进行比较:
1
2
3
plt.scatter(iris.data[iris.target == 0, 2], iris.data[iris.target == 0, 3], s=100, c='red', label='Cluster1')
plt.scatter(iris.data[iris.target == 1, 2], iris.data[iris.target == 1, 3], s=100, c='blue', label='Cluster2')
plt.scatter(iris.data[iris.target == 2, 2], iris.data[iris.target == 2, 3], s=100, c='green', label='Cluster3')
2.linkage
1
def linkage(y, method='single', metric='euclidean', optimal_ordering=False)
参数详解:
y:可以是一维或二维矩阵。method:详见本博文第3部分。metric:初始距离矩阵$D_1$的计算方式(见第3部分)。optimal_ordering:如果为True,linkage matrix会重新排序,以使树状图的连续叶子结点之间的距离最小。
举个例子:
1
2
3
4
5
6
7
8
9
from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
from matplotlib import pyplot as plt
X = [[i] for i in [2, 8, 0, 4, 1]]
Z = linkage(X, method='single', metric='euclidean')
print(Z)
f = fcluster(Z,4,'distance')
fig = plt.figure(figsize=(5, 3))
dn = dendrogram(Z)
plt.show()

注意这里绘制的树状图和第3部分引用wiki百科例子中的树状图稍有不同。
linkage返回的Z是一个矩阵:
1
2
3
4
[[0. 4. 1. 2.]
[2. 5. 1. 3.]
[3. 6. 2. 4.]
[1. 7. 4. 5.]]
Z中第1列和第2列为每一步聚合的两个簇,第3列为这两个簇的距离,第4列为聚合之后的新簇包含的元素个数。
接下来我们来仔细看下Z中的每一行是怎么来的。构建距离矩阵$D_1$($C0,C1,C2,C3,C4$对应X中的元素$[2,8,0,4,1]$,其中$C0$表示第0个簇,即Z中前两列中的0,$D_1$的计算采用欧式距离):
| C0 | C1 | C2 | C3 | C4 | |
|---|---|---|---|---|---|
| C0 | 0 | 6 | 2 | 2 | 1 |
| C1 | 6 | 0 | 8 | 4 | 7 |
| C2 | 2 | 8 | 0 | 4 | 1 |
| C3 | 2 | 4 | 4 | 0 | 3 |
| C4 | 1 | 7 | 1 | 3 | 0 |
$C0$和$C4$的距离最近($d(C0,C4)=1$),将其聚成一类,记为$C5=(C0,C4)$。计算$C5$到其他剩余簇的距离(这里采用single方法):
\[D_2(C5,C1)=\min(D_1(C0,C1),D_1(C4,C1))=\min(6,7)=6\] \[D_2(C5,C2)=\min(D_1(C0,C2),D_1(C4,C2))=\min(2,1)=1\] \[D_2(C5,C3)=\min(D_1(C0,C3),D_1(C4,C3))=\min(2,3)=2\]该函数绘制的树状图中,$C0$和$C4$聚成的节点到$C0$或$C4$的距离是1,而在wiki百科的例子中,$C0$和$C4$聚成的节点到$C0$或$C4$的距离是$1/2=0.5$。
更新距离矩阵$D_2$:
| C5 | C1 | C2 | C3 | |
|---|---|---|---|---|
| C5 | 0 | 6 | 1 | 2 |
| C1 | 6 | 0 | 8 | 4 |
| C2 | 1 | 8 | 0 | 4 |
| C3 | 2 | 4 | 4 | 0 |
$C5$和$C2$距离最近($d(C5,C2)=1$),将其聚成$C6=(C5,C2)$。计算$C6$到剩余其他簇的距离:
\[D_3(C6,C1)=\min (D_2(C5,C1),D_2(C2,C1))=\min(6,8)=6\] \[D_3(C6,C3)=\min (D_2(C5,C3),D_2(C2,C3))=\min(2,4)=2\]更新距离矩阵$D_3$:
| C6 | C1 | C3 | |
|---|---|---|---|
| C6 | 0 | 6 | 2 |
| C1 | 6 | 0 | 4 |
| C3 | 2 | 4 | 0 |
$C6$和$C3$距离最近($d(C6,C3)=2$),将其聚成$C7=(C6,C3)$。最后聚合剩余的两个簇$C7$和$C1$:
\[D_4(C7,C1)=\min (D_3(C6,C1),D_3(C3,C1))=\min(6,4)=4\]距离矩阵$D_4$:
| C7 | C1 | |
|---|---|---|
| C7 | 0 | 4 |
| C1 | 4 | 0 |
3.method
该函数提供了多种聚类中常用的计算簇之间距离的方式。接下来一个一个介绍。
3.1.single
详见【机器学习基础】第三十七课:聚类之层次聚类中的“single-linkage”。也被称为the Nearest Point Algorithm。举个例子,假设我们有5个样本:$a,b,c,d,e$,其之间的距离矩阵$D_1$见下:

距离最近的两个样本是$D_1(a,b)=17$。此时,我们便可以合并样本$a$和$b$,树状图中的节点$u$就表示$a$和$b$已经连接了,然后设$\delta(a,u)=\delta(b,u)=D_1 (a,b)/2=8.5$,以确保$a,b$到$u$的距离是相等的(其实$a,b$到$u$的距离就是到簇质心的距离):
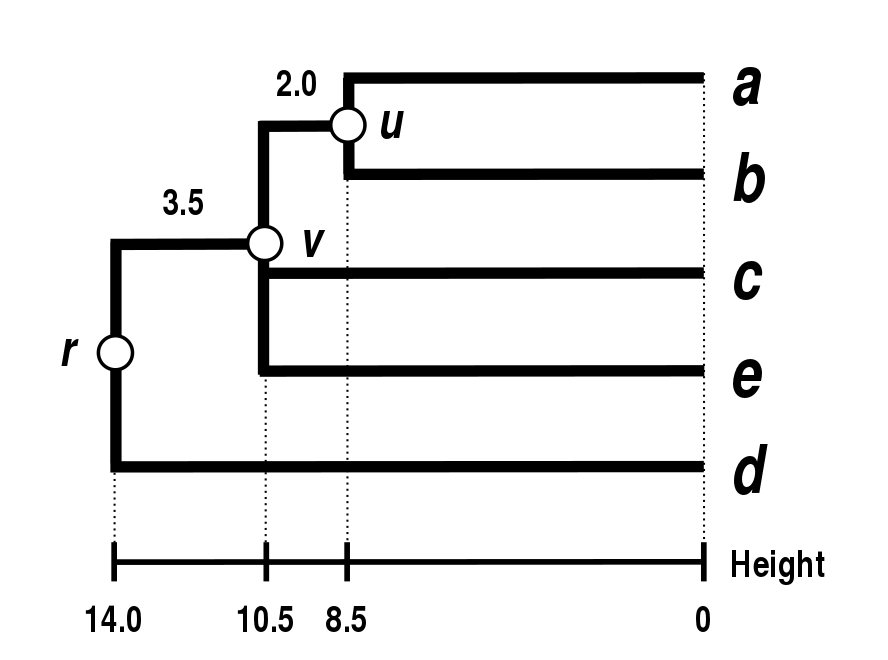
然后分别计算簇$(a,b)$到$c,d,e$的距离:
\[D_2((a,b),c)=\min(D_1(a,c),D_1(b,c))=\min (21,30)=21\] \[D_2((a,b),d)=\min(D_1(a,d),D_1(b,d))=\min (31,34)=31\] \[D_2((a,b),e)=\min(D_1(a,e),D_1(b,e))=\min (23,21)=21\]更新距离矩阵$D_2$:
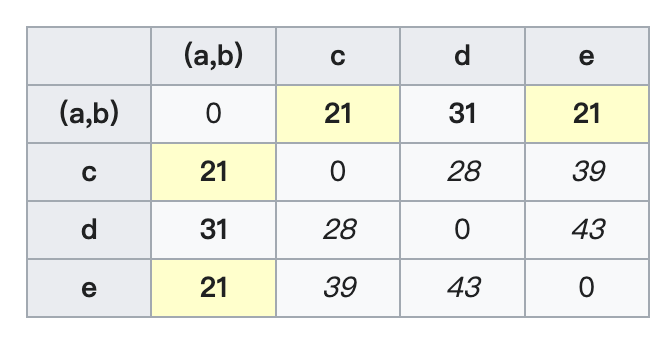
最近的距离有两个:$D_2((a,b),c)$和$D_2((a,b),e)$。因此,我们合并$(a,b),c,e$。节点$v$的总长度为$\delta(a,v)=\delta(b,v)=\delta(c,v)=\delta(e,v)=21/2=10.5$。因此可算得:$\delta(u,v)=\delta(c,v)-\delta(a,u)=\delta(c,v)-\delta(b,u)=10.5-8.5=2$。然后计算簇$((a,b),c,e)$和剩余簇$d$的距离:
\[D_3(((a,b),c,e),d)=\min(D_2((a,b),d),D_2(c,d),D_2(e,d))=\min(31,28,43)=28\]更新距离矩阵$D_3$:
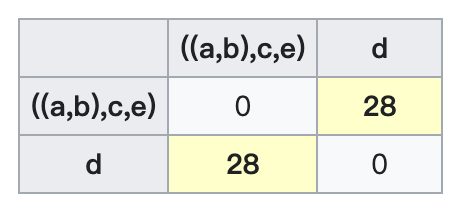
和上面一样的策略,计算节点$r$的总长度:$\delta(((a,b),c,e),r)=\delta(d,r)=28/2=14$。同理可算得:$\delta(v,r)=\delta(a,r)-\delta(a,v)=\delta(b,r)-\delta(b,v)=\delta(c,r)-\delta(c,v)=\delta(e,r)-\sigma(e,v)=14-10.5=3.5$。至此,整个聚类过程和树状图的绘制全部结束。
3.2.complete
详见【机器学习基础】第三十七课:聚类之层次聚类中的“complete-linkage”。也被称为the Farthest Point Algorithm或Voor Hees Algorithm。依旧以以下距离矩阵$D_1$为例:

依然是$a,b$距离最近($D_1(a,b)=17$),现将这两个样本聚为一个簇。节点$u$:
\[\delta(a,u)=\delta(b,u)=17/2=8.5\]计算簇$(a,b)$到其他簇的距离:
\[D_2((a,b),c)=\max(D_1(a,c),D_1(b,c))=\max(21,30)=30\] \[D_2((a,b),d)=\max(D_1(a,d),D_1(b,d))=\max(31,34)=34\] \[D_2((a,b),e)=\max(D_1(a,e),D_1(b,e))=\max(23,21)=23\]更新距离矩阵$D_2$:
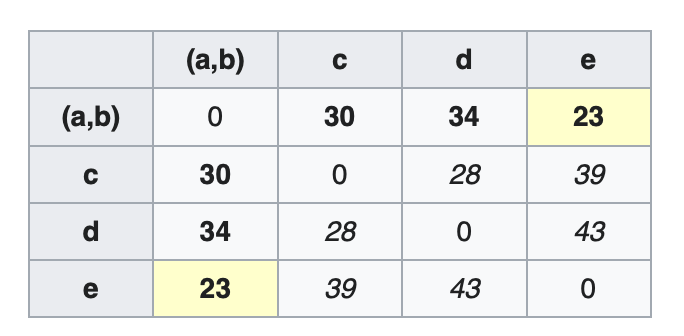
将距离最近的$(a,b)$和$e$聚在一起($D_2((a,b),e)=23$)。节点$v$:
\[\delta(a,v)=\delta(b,v)=\delta(e,v)=23/2=11.5\] \[\delta(u,v)=\delta(e,v)-\delta(a,u)=\delta(e,v)-\delta(b,u)=11.5-8.5=3\]计算簇$((a,b),e)$到其他簇的距离:
\[D_3(((a,b),e),c)=\max(D_2((a,b),c),D_2(e,c))=\max(30,39)=39\] \[D_3(((a,b),e),d)=\max(D_2((a,b),d),D_2(e,d))=\max(34,43)=43\]更新距离矩阵$D_3$:
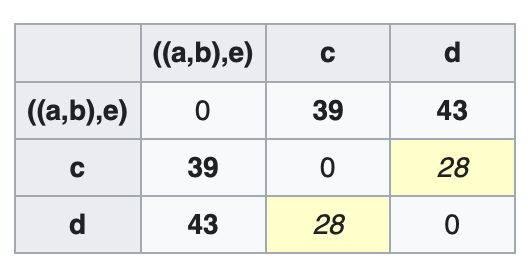
$c,d$的距离最近($D_3(c,d)=28$),将其聚成一类。节点$w$:
\[\delta(c,w)=\delta(d,w)=28/2=14\]计算最后两个簇$((a,b),e)$和$(c,d)$之间的距离:
\[D_4((c,d),((a,b),e))=\max(D_3(c,((a,b),e)),D_3(d,((a,b),e)))=\max(39,43)=43\]更新距离矩阵$D_4$:
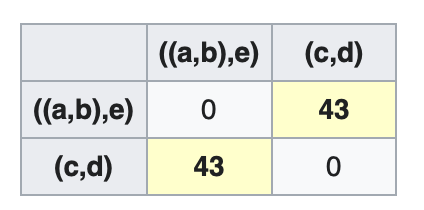
节点$r$:
\[\delta(((a,b),e),r)=\delta((c,d),r)=43/2=21.5\] \[\delta(v,r)=\delta(((a,b),e),r)-\delta(e,v)=21.5-11.5=10\] \[\delta(w,r)=\delta((c,d),r)-\delta(c,w)=21.5-14=7.5\]最终的树状图见下:
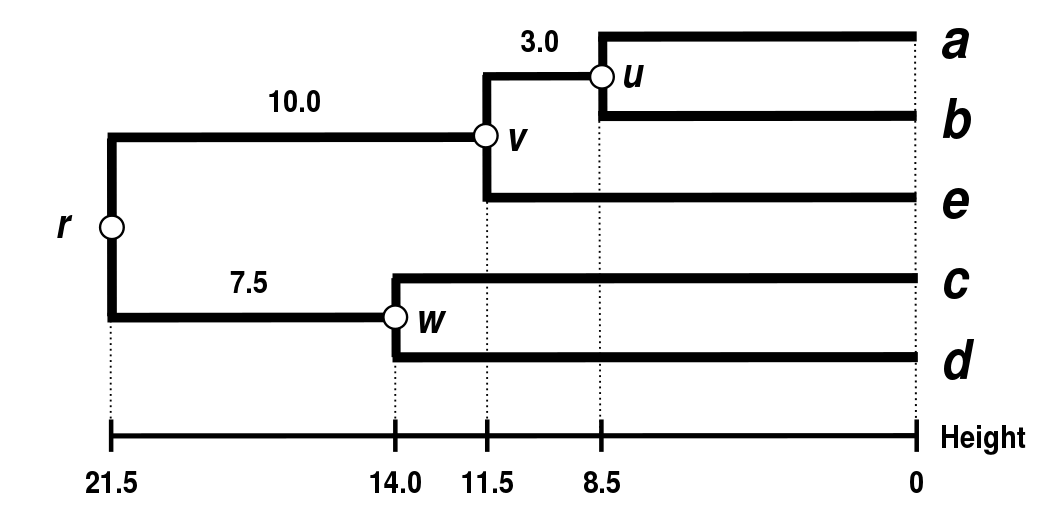
3.3.average
详见【机器学习基础】第三十七课:聚类之层次聚类中的“average-linkage”。也被称为the UPGMA (unweighted pair group method with arithmetic mean) algorithm。以以下距离矩阵$D_1$为例:

$a,b$距离最近$D_1(a,b)=17$,先聚成一类。节点$u$:
\[\delta(a,u)=\delta(b,u)=17/2=8.5\]计算簇$(a,b)$到其他簇的距离:
\[D_2((a,b),c)=\frac{D_1(a,c) \times 1 + D_1(b,c) \times 1}{1+1}=\frac{21+30}{2}=25.5\] \[D_2((a,b),d)=\frac{D_1(a,d)+D_1(b,d)}{2}=\frac{31+34}{2}=32.5\] \[D_2((a,b),e)=\frac{D_1(a,e)+D_1(b,e)}{2}=\frac{23+21}{2}=22\]更新距离矩阵$D_2$:
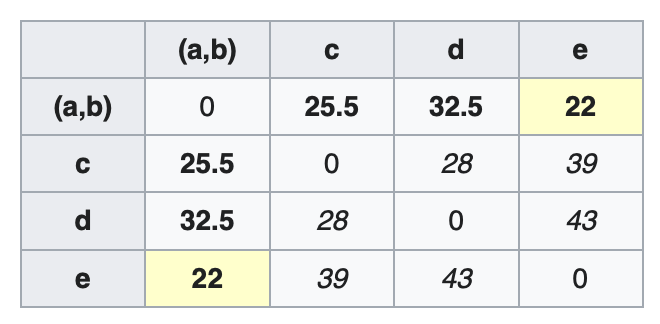
$(a,b)$和$e$的距离最近($D_2((a,b),e)=22$),聚成一类。节点$v$:
\[\delta(a,v)=\delta(b,v)=\delta(e,v)=22/2=11\] \[\delta(u,v)=\delta(e,v)-\delta(a,u)=\delta(e,v)-\delta(b,u)=11-8.5=2.5\]计算簇$((a,b),e)$到其他簇的距离(⚠️注意此时的系数):
\[D_3(((a,b),e),c)=\frac{D_2((a,b),c)\times 2+D_2(e,c)\times 1}{2+1}=\frac{25.5\times 2+39\times 1}{3}=30\] \[D_3(((a,b),e),d)=\frac{D_2((a,b),d)\times 2 + D_2(e,d)\times 1}{2+1}=\frac{32.5\times 2+43\times 1}{3}=36\]此时的系数是$2:1$,是因为$D_2((a,b),c)$和$D_2(e,c)$相比,$(a,b)$有两个元素而$e$只有一个元素。每个元素的权值都是1,所以该方法称为是unweighted的。
更新距离矩阵$D_3$:

此时,$c,d$的距离最近($D_3(c,d)=28$),将其聚成一类。节点$w$:
\[\delta(c,w)=\delta(d,w)=28/2=14\]计算最后两个簇$(c,d)$和$((a,b),e)$之间的距离:
\[D_4((c,d),((a,b),e))=\frac{D_3(c,((a,b),e))\times 1 + D_3 (d,((a,b),e))\times 1}{1+1}=\frac{30\times 1+36\times 1}{2}=33\]此时的系数是$1:1$,是因为$D_3(c,((a,b),e))$和$D_3 (d,((a,b),e))$中的元素数量是相等的。
更新距离矩阵$D_4$:

最后一步便是把簇$((a,b),e)$和簇$(c,d)$聚在一起。节点$r$:
\[\delta(((a,b),e),r)=\delta((c,d),r)=33/2=16.5\] \[\delta(v,r)=\delta(((a,b),e),r)-\delta(e,v)=16.5-11=5.5\] \[\delta(w,r)=\delta((c,d),r)-\delta(c,w)=16.5-14=2.5\]最终得到的树状图:
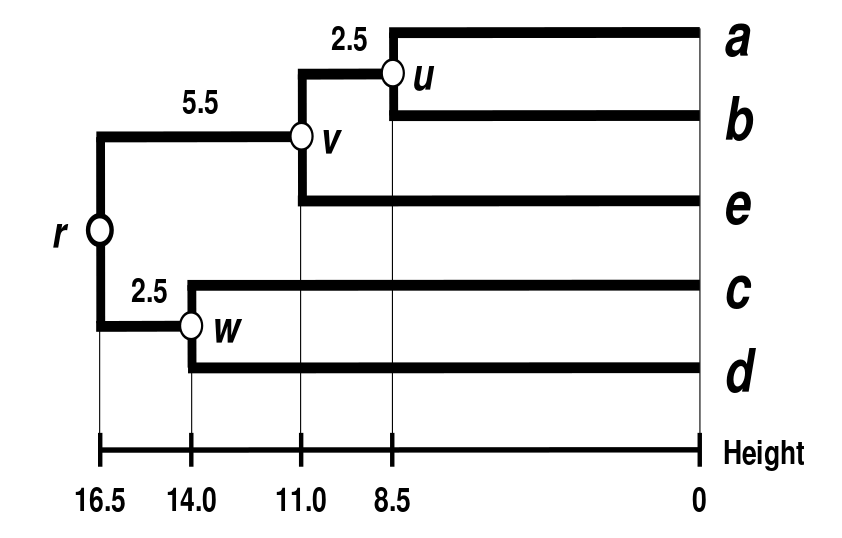
3.4.weighted
在每一步中,距离最近的两个簇$i$和$j$会合并为一个higher-level的簇$i \cup j$,然后这个higher-level的簇到另一个簇$k$的距离计算为:
\[d_{(i \cup j),k}=\frac{d_{i,k}+d_{j,k}}{2}\]该方式也称为WPGMA (Weighted Pair Group Method with Arithmetic Mean)。以距离矩阵$D_1$为例:

$a,b$距离最近($D_1(a,b)=17$),最先聚成一类。节点$u$:
\[\delta(a,u)=\delta(b,u)=17/2=8.5\]计算簇$(a,b)$到其他簇的距离:
\[D_2((a,b),c)=\frac{D_1(a,c) + D_1(b,c)}{2}=\frac{21+30}{2}=25.5\] \[D_2((a,b),d)=\frac{D_1(a,d)+D_1(b,d)}{2}=\frac{31+34}{2}=32.5\] \[D_2((a,b),e)=\frac{D_1(a,e)+D_1(b,e)}{2}=\frac{23+21}{2}=22\]更新距离矩阵$D_2$:

$(a,b)$和$e$的距离最近($D_2((a,b),e)=22$),聚成一类。节点$v$:
\[\delta(a,v)=\delta(b,v)=\delta(e,v)=22/2=11\] \[\delta(u,v)=\delta(e,v)-\delta(a,u)=\delta(e,v)-\delta(b,u)=11-8.5=2.5\]计算簇$((a,b),e)$到其他簇的距离(⚠️注意此时的系数):
\[D_3(((a,b),e),c)=\frac{D_2((a,b),c)+D_2(e,c)}{2}=\frac{25.5+39}{2}=32.25\] \[D_3(((a,b),e),d)=\frac{D_2((a,b),d)+ D_2(e,d)}{2}=\frac{32.5+43}{2}=37.75\]这一步显示出了UPGMA和WPGMA的不同之处。WPGMA对于含不同数量元素的簇都一视同仁,这就相当于是对单个元素进行了加权。
更新距离矩阵$D_3$:
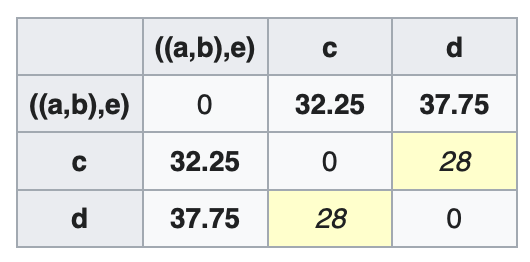
$c,d$的距离最近($D_3(c,d)=28$),聚成一类。节点$w$:
\[\delta(c,w)=\delta(d,w)=28/2=14\]计算最后两个簇$(c,d)$和$((a,b),e)$之间的距离:
\[D_4((c,d),((a,b),e))=\frac{D_3(c,((a,b),e))+D_3(d,((a,b),e))}{2}=\frac{32.25+37.75}{2}=35\]更新距离矩阵$D_4$:
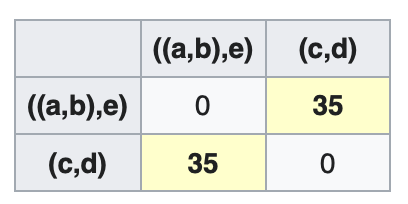
节点$r$:
\[\delta(((a,b),e),r)=\delta((c,d),r)=35/2=17.5\] \[\delta(v,r)=\delta(((a,b),e),r)-\delta(e,v)=17.5-11=6.5\] \[\delta(w,r)=\delta((c,d),r)-\delta(c,w)=17.5-14=3.5\]最终得到的树状图:
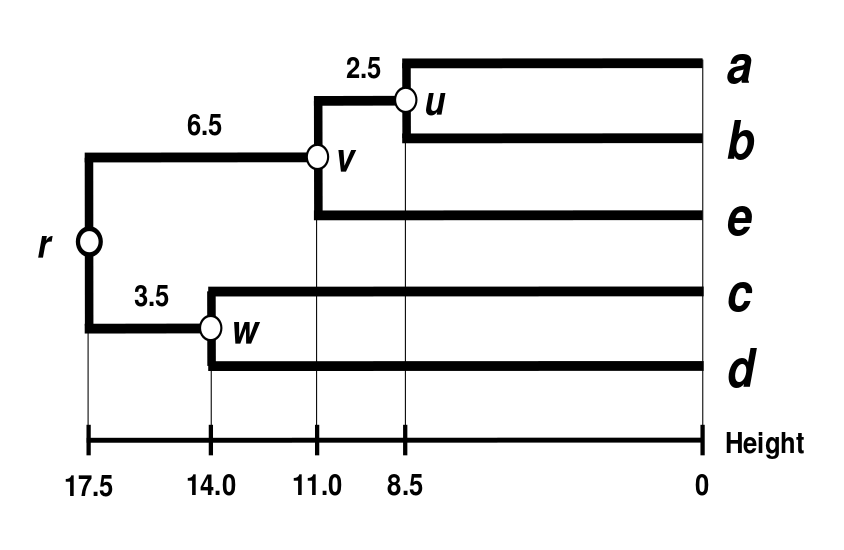
3.5.centroid
两个簇之间的距离定义为两个簇质心之间的距离。该方法称为UPGMC(Unweighted Pair Group Method with Centroid)。
3.6.median
同样是将两个簇之间的距离定义为两个簇质心之间的距离。该方法称为WPGMC(Weighted Pair Group Method with Centroid)。WPGMC和UPGMC的区别可类比WPGMA和UPGMA。
3.7.ward
使用Ward variance minimization算法(Ward’s minimum variance method)。该方法的目标是最小化簇内方差之和(minimizes the total within-cluster variance)。在每一步,该方法都会尝试聚合两个簇,且使聚合之后的总簇内方差增长最小。初始状态下,单个样本之间的距离定义为欧式距离的平方:
\[d_{ij}=d(\{ X_i \},\{X_j \}) = \parallel X_i - X_j \parallel ^2\]即之前部分提到的距离矩阵$D_1$的计算。
Ward’s minimum variance method可定义为Lance–Williams algorithm的递归实现。假设接下来需要聚合的两个簇为$C_i$和$C_j$。用$d_{ij},d_{ik},d_{jk}$分别表示簇$C_i,C_j,C_k$之间的距离。用$d_{(ij)k}$表示簇$C_i \cup C_j$和簇$C_k$之间的距离。Lance–Williams algorithm通常定义:
\[d_{(ij)k}=\alpha_i d_{ik}+\alpha_j d_{jk} + \beta d_{ij} + \gamma \lvert d_{ik}-d_{jk} \rvert\]Ward’s minimum variance method将参数$\alpha_i,\alpha_j,\beta,\gamma$定义为:
\[\alpha_i=\frac{n_i + n_k}{n_i + n_j + n_k}, \alpha_j = \frac{n_j + n_k}{n_i + n_j + n_k},\beta=\frac{-n_k}{n_i+n_j+n_k},\gamma=0\]即:
\[d(C_i \cup C_j,C_k)=\frac{n_i + n_k}{n_i + n_j + n_k} d(C_i,C_k)+\frac{n_j + n_k}{n_i + n_j + n_k} d(C_j,C_k)-\frac{n_k}{n_i+n_j+n_k} d(C_i,C_j)\]$n$为簇的size。