本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.图像特征
图像特征:可以表达图像中对象的主要信息,并且以此为依据可以从其他未知图像中检测出相似或者相同对象。
常见的图像特征:边缘、角点、纹理。
2.Harris角点检测
首先解释下角点的概念。如果我们在图像上滑动一个小窗口:
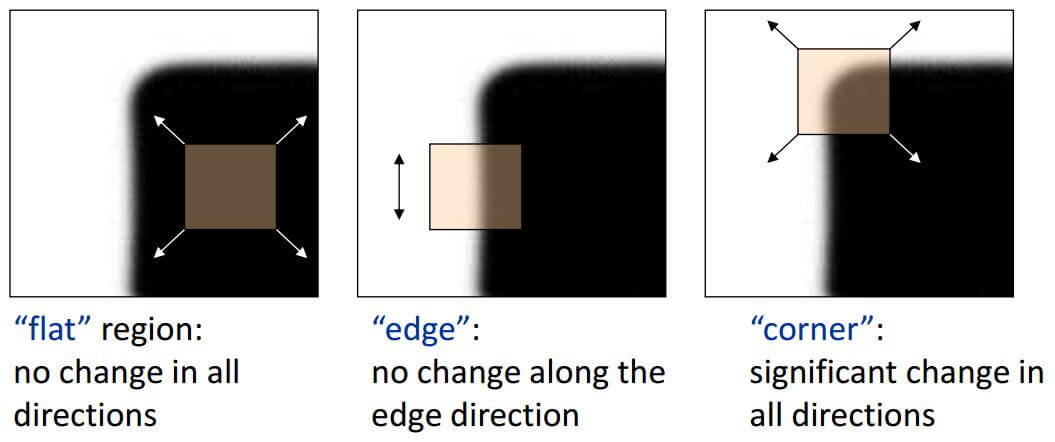
- 如果在任何方向上滑动窗口,窗口内的灰度都没什么变化,则这是一个均匀区域。
- 如果窗口内的灰度只在一个方向上滑动时才会有变化,则这可能是一个边缘。
- 如果在任何方向上滑动窗口,窗口内的灰度都会发生变化,则这是一个角点。
角点检测的主要应用有:图像对齐、图像拼接、目标识别、3D重建、运动跟踪等。
检测角点的算法有很多,本文主要介绍最为基础的Harris角点检测。
首先我们来定义灰度的变化。假设滑动窗口的中心位于图像的$(x,y)$位置,该位置的灰度值为$I(x,y)$。将窗口向$x$方向和$y$方向分别位移$u$个单位和$v$个单位,此时窗口中心的坐标为$(x+u,y+v)$,这个位置的灰度值为$I(x+u,y+v)$。则因窗口滑动而导致的窗口中心点的灰度变化为:
\[I(x+u,y+v)-I(x,y) \tag{1}\]假设我们考虑窗口内的所有点,给每个点赋予权值$w$,则窗口滑动得到的总的灰度变化为:
\[E(u,v)=\sum_{(x,y)} w(x,y) \times [ I(x+u,y+v)-I(x,y) ]^2 \tag{2}\]权重矩阵通常我们可以采用二维高斯分布。我们使用二元函数的一阶泰勒展开进行如下近似化简:
\[I(x+u,y+v) \approx I(x,y) + I_x(x,y)u + I_y (x,y) v \tag{3}\]其中$I_x$和$I_y$是$I$的偏微分,在图像中就是在$x$和$y$方向的梯度图(可以使用Sobel算子得到):
\[I_x = \frac{\partial I(x,y)}{\partial x}, I_y=\frac{\partial I(x,y)}{\partial y} \tag{4}\]把式(3)代入式(2):
\[\begin{align} E(u,v) &= \sum_{(x,y)} w(x,y) \times [ I(x+u,y+v)-I(x,y) ]^2 \\& \approx \sum_{(x,y)} w(x,y) \times [I(x,y) + I_x u + I_y v - I(x,y) ]^2 \\&= \sum_{(x,y)} w(x,y) \times (I_x u + I_y v) ^2 \\&= \sum_{(x,y)} w(x,y) \times (u^2 I^2_x + v^2 I^2_y + 2uvI_xI_y) \end{align} \tag{5}\]把$u,v$提出来:
\[E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix} \tag{6}\]其中,
\[M=\sum_{(x,y)} w(x,y) \begin{bmatrix} I^2_x & I_x I_y \\ I_x I_y & I^2_y \end{bmatrix} = \begin{bmatrix} \sum_{(x,y)} w(x,y) I^2_x & \sum_{(x,y)} w(x,y) I_x I_y \\ \sum_{(x,y)} w(x,y) I_x I_y & \sum_{(x,y)} w(x,y) I^2_y \end{bmatrix} \tag{7}\]对矩阵$M$进行实对称矩阵的正交相似对角化(见本文第2.1部分):
\[\begin{align} E(u,v) &\approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix} \\&= \begin{bmatrix} u & v \end{bmatrix} P \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} P^T \begin{bmatrix} u \\ v \end{bmatrix} \\&= \begin{bmatrix} u' & v' \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} \begin{bmatrix} u' \\ v' \end{bmatrix} \\&= \lambda_1 (u')^2 + \lambda_2 (v')^2 \\&= \frac{(u')^2}{\frac{1}{\lambda_1}} + \frac{(v')^2}{\frac{1}{\lambda_2}} \end{align}\tag{8}\]其中,$\lambda_1,\lambda_2$为矩阵$M$的特征值。根据【数学基础】第十五课:矩阵的相似变换和相合变换一文和本文第2.2部分,我们知道相似矩阵的几何意义就是同一个线性变换在不同的基下的表达形式。所以式(8)相当于是换了一组基,此时我们得到了一个标准的椭圆方程(椭圆相关内容见本文第2.3部分):
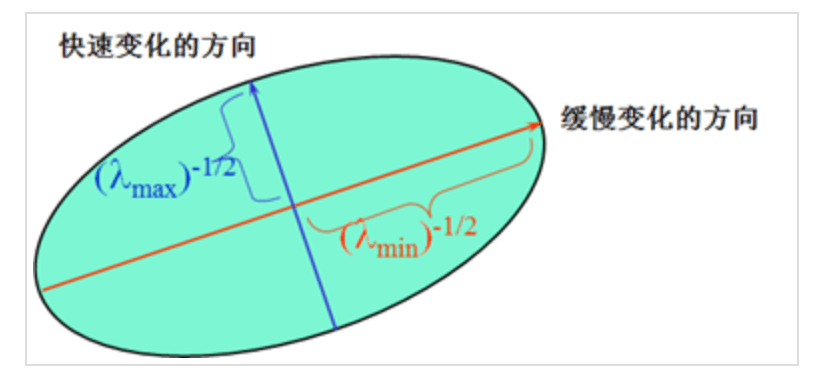
上图中,$\lambda_{max}=\max(\lambda_1,\lambda_2),\lambda_{min}=\min(\lambda_1,\lambda_2)$。
如果$\lambda_1,\lambda_2$只有一个很大,则意味着(在新基下)只沿着一个方向,$E(u,v)$会发生较大变化,所以这很有可能是个边缘,而不是角点。只有$\lambda_1,\lambda_2$都很大,即无论沿着哪个方向,$E(u,v)$都会发生较大变化,这才非常有可能是一个角点:
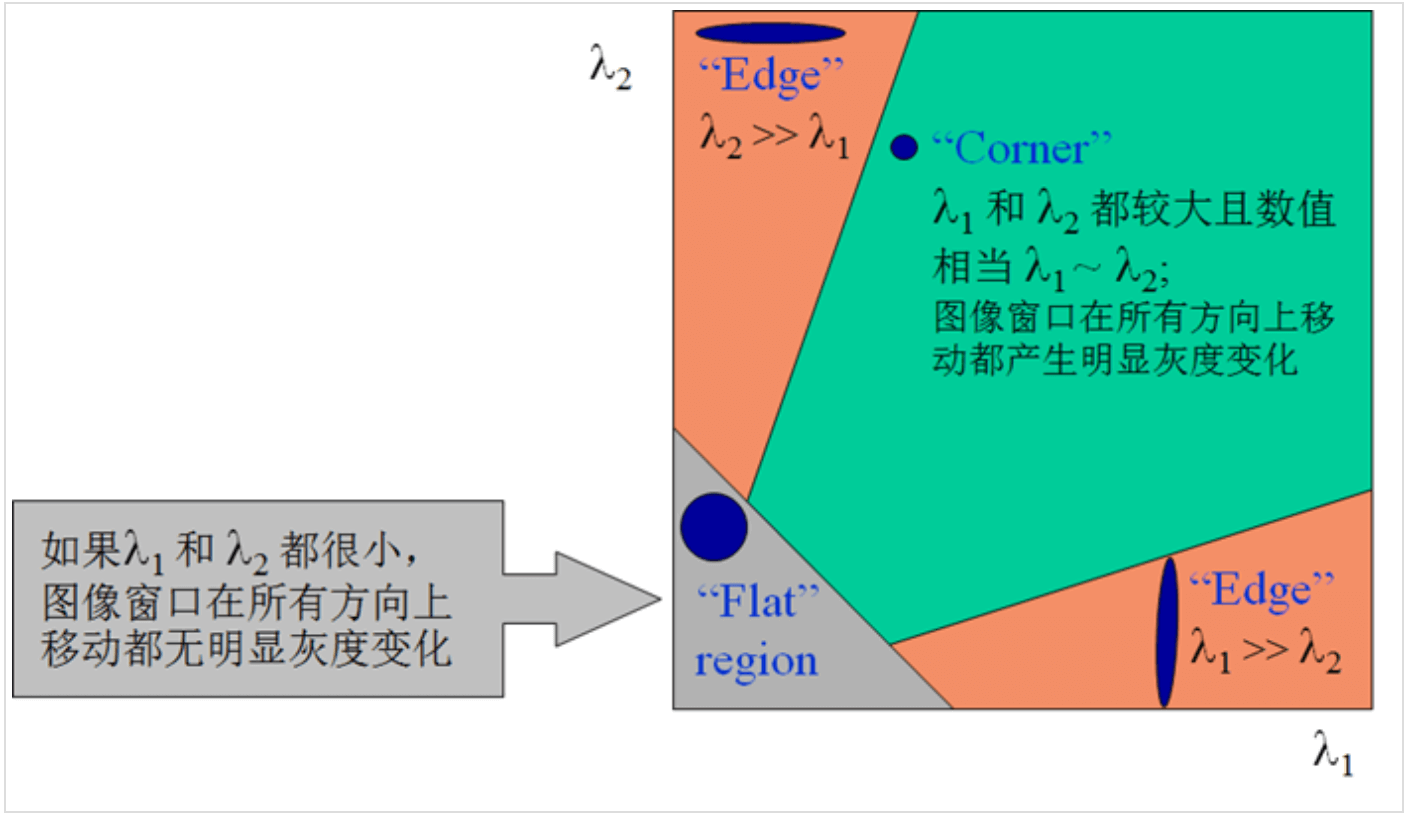
而在实际计算时,我们并不真的计算矩阵$M$的特征值,而是构建一个响应函数$R$:
\[R=\text{det}(M)-k * (\text{trace}(M))^2\]其中,$\text{det}(M)=\lambda_1 \lambda_2$为矩阵$M$的行列式,$\text{trace}(M)=\lambda_1+\lambda_2$是矩阵$M$的迹。
特征值和矩阵行列式、迹之间的关系:【数学基础】第十五课:矩阵的相似变换和相合变换。
$k$是一个经验常数,范围通常在$(0.04,0.06)$之间。Harris角点检测的结果是带有这些分数$R$的灰度图像,设定一个阈值,分数大于这个阈值的像素就对应角点。
⚠️Harris检测器具有旋转不变性,但不具有尺度不变性,也就是说尺度变化可能会导致角点变为边缘,例如:
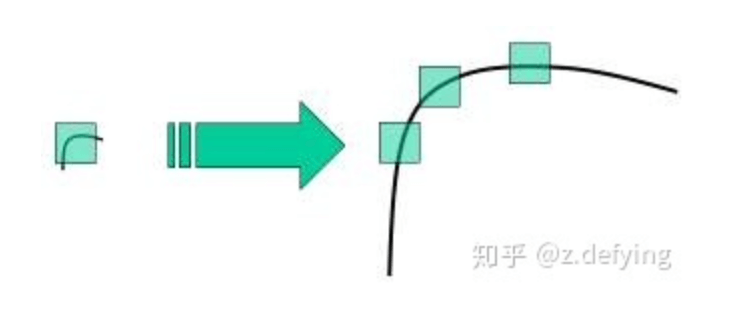
尺度不变性可使用SIFT特征。
2.1.实对称矩阵的对角化
👉实对称矩阵:如果有$n$阶矩阵$A$,其矩阵的元素都为实数,且矩阵$A$的转置等于其本身,则称$A$为实对称矩阵。
实对称矩阵有以下主要性质:
- 实对称矩阵$A$的不同特征值对应的特征向量是正交的。
- 实对称矩阵$A$的特征值都是实数。
- $n$阶实对称矩阵$A$必可相似对角化,且相似对角阵上的元素即为矩阵本身特征值。
- 若$A$具有$k$重特征值$\lambda_0$,则必有$k$个线性无关的特征向量。
- 实对称矩阵$A$一定可以正交相似对角化。
👉对角化,相似对角化,正交相似对角化(查阅了一些资料,对这三个概念的理解如下,如有误,欢迎大家指正):
查阅的资料中对于对角化的解释有两种。第一种:对角化指的就是相似对角化。第二种:矩阵$A$的对角化指的是存在可逆矩阵$P,Q$,使得$PAQ$为对角矩阵。
矩阵的相似对角化就是,对于方阵$A$,存在相似变换矩阵$P$,使得$P^{-1}AP=\Lambda$,$\Lambda$为对角矩阵。
正交相似对角化:对于$n$阶实对称矩阵,一定会有正交矩阵$Q$,使得:
\[Q^{-1}AQ=Q^TAQ=\Lambda\]$\Lambda$为对角矩阵。
2.2.相似矩阵的几何意义
本人之前写过的相关博客:【数学基础】第十五课:矩阵的相似变换和相合变换。
设$A,B$都是$n$阶方阵,若有可逆矩阵$P$,使得:
\[B=P^{-1}AP\]则称$P$为相似变换矩阵,称$B$是$A$的相似矩阵,记作:
\[A \simeq B\]我们知道,线性映射是将一个向量映射到另一个向量,比如这里将$\mathbf{x}$映射成$\mathbf{y}$:

将$\mathbf{x}$在自然基下的坐标向量用$[\mathbf{x}]_{\epsilon}$表示,$\mathbf{y}$在自然基下的坐标向量用$[\mathbf{y}]_{\epsilon}$表示。矩阵$A$就是将坐标向量$[\mathbf{x}]_{\epsilon}$映射到坐标向量$[\mathbf{y}]_{\epsilon}$:
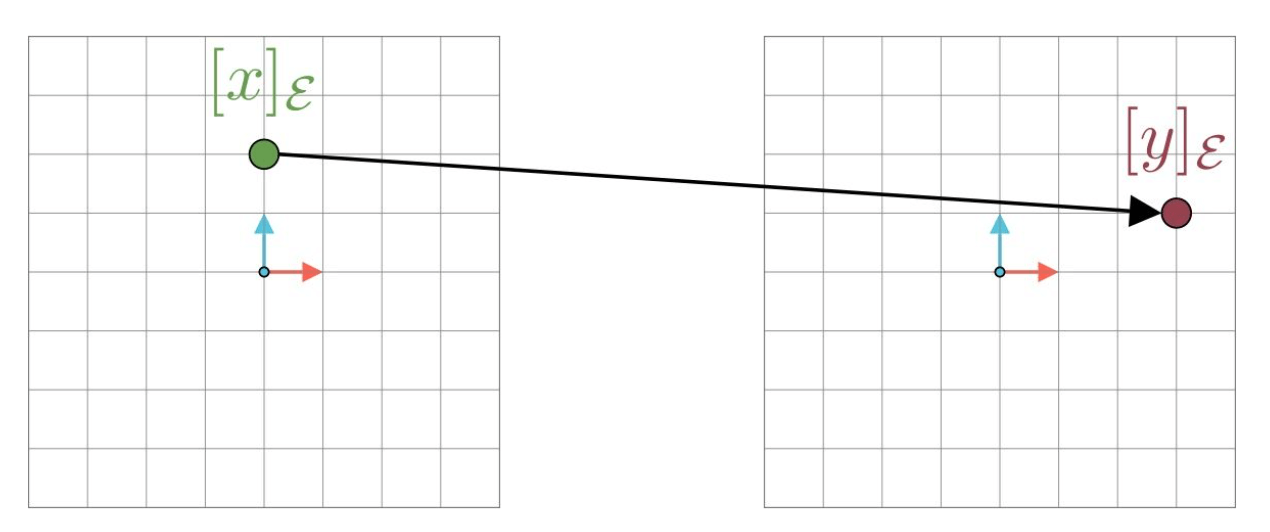
这里坐标向量$[\mathbf{x}]_{\epsilon}=\begin{pmatrix} 0 \\ 2 \end{pmatrix}$,坐标向量$[\mathbf{y}]_{\epsilon}=\begin{pmatrix} 3 \\ 1 \end{pmatrix}$,矩阵$A$就是把$\begin{pmatrix} 0 \\ 2 \end{pmatrix}$转换为$\begin{pmatrix} 3 \\ 1 \end{pmatrix}$:
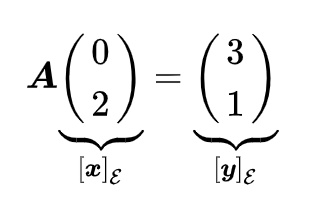
还是将$\mathbf{x}$映射成$\mathbf{y}$,现在将这个映射表示在非自然基下:

将$\mathbf{x}$在非自然基下的坐标向量用$[\mathbf{x}]_{\mathcal{P}}$表示,$\mathbf{y}$在非自然基下的坐标向量用$[\mathbf{y}]_{\mathcal{P}}$表示。矩阵$B$就是将坐标向量$[\mathbf{x}]_{\mathcal{P}}$映射到坐标向量$[\mathbf{y}]_{\mathcal{P}}$:
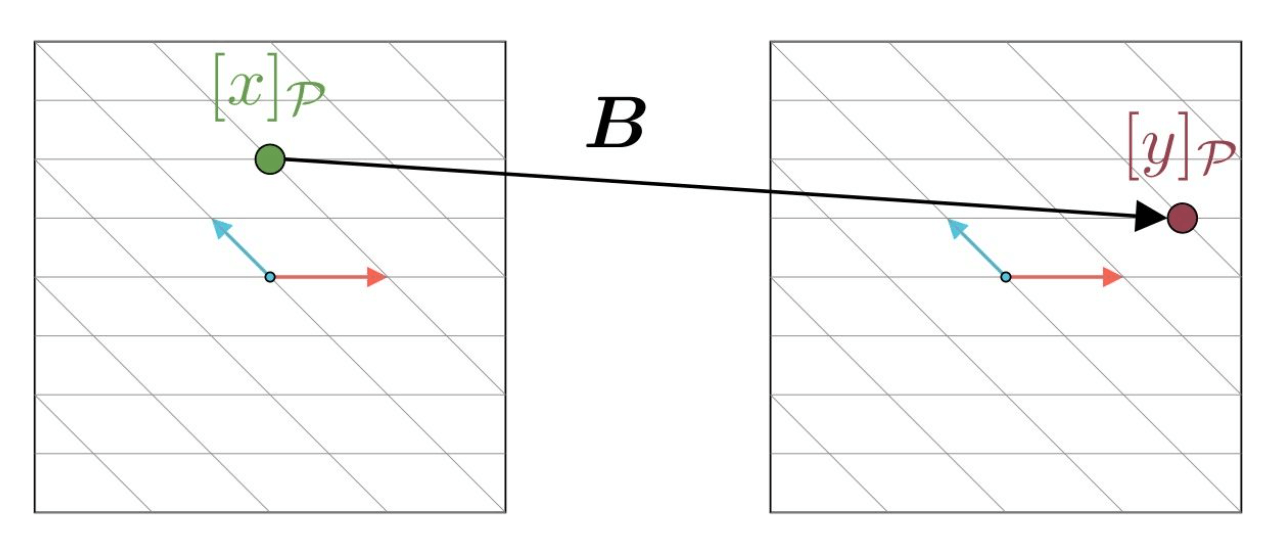
这里坐标向量$[\mathbf{x}]_{\mathcal{P}} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}, [\mathbf{y}]_{\mathcal{P}} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}$。矩阵$B$就是把$\begin{pmatrix} 1 \\ 2 \end{pmatrix}$转换为$\begin{pmatrix} 2 \\ 1 \end{pmatrix}$:

也就是说矩阵$A$,矩阵$B$,都是将$\mathbf{x}$映射到向量$\mathbf{y}$,而它们只是不同基下的不同代数表达。
假如我们可以通过某矩阵$P$,将坐标向量$[\mathbf{x}]_{\mathcal{P}}$变换为坐标向量$[\mathbf{x}]_{\epsilon}$;矩阵$P^{-1}$,将坐标向量$[\mathbf{y}]_{\epsilon}$变换为坐标向量$[\mathbf{y}]_{\mathcal{P}}$:
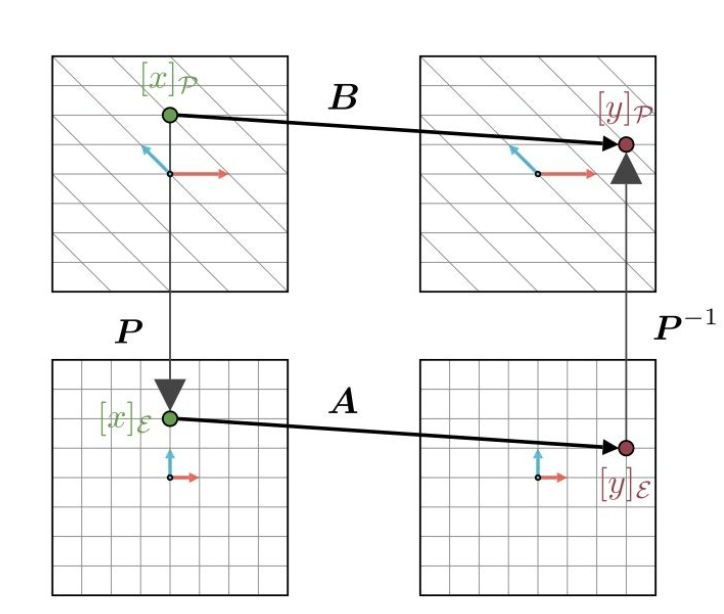
这个时候$B$和$P^{-1}AP$都是将$[\mathbf{x}]_{\mathcal{P}}$映射为$[\mathbf{y}]_{\mathcal{P}}$,因此它们是相等的,即:
\[B=P^{-1}AP\]2.3.椭圆
椭圆的第一定义:平面内与两定点$F_1,F_2$的距离的和等于常数$2a$($2a > \lvert F_1F_2 \rvert$)的动点$P$的轨迹叫做椭圆。即:
\[\lvert PF_1 \rvert + \lvert PF_2 \rvert = 2a\]其中两定点$F_1,F_2$叫做椭圆的焦点,两焦点的距离$\lvert F_1F_2 \rvert=2c<2a$叫做椭圆的焦距。$P$为椭圆的动点。
椭圆截与两焦点连线重合的直线所得的弦为长轴,长度为$2a$ 。椭圆截垂直平分两焦点连线的直线所得弦为短轴,长度为$2b$。

椭圆的标准方程(这里的“标准”指的是中心在原点,对称轴为坐标轴)有两种:
- 焦点在$X$轴时,标准方程为:$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1(a>b>0)$。
- 焦点在$Y$轴时,标准方程为:$\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1(a>b>0)$。
3.cv::cornerHarris
1
2
3
4
5
6
7
8
void cornerHarris(
InputArray src,
OutputArray dst,
int blockSize,
int ksize,
double k,
int borderType = BORDER_DEFAULT
);
参数详解:
InputArray src:输入图像,为单通道8-bit或floating-point图像。OutputArray dst:输出图像,和输入图像大小一样,类型为CV_32FC1。图像存储的是响应值$R$。int blockSize:滑动窗口的大小。int ksize:用于计算梯度的sobel算子的尺寸。double k:响应函数$R$中的$k$值。int borderType:边界填充方式,详见:【OpenCV基础】第十五课:边缘处理。