本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
人体姿态估计(Human Pose Estimation)是计算机视觉领域的一个基础问题,用于检测人体关节点的空间位置(比如坐标)。人体姿态估计是一个非常重要且有一定难度的任务,因为会有不同风格的衣服、各种形式的遮挡以及不受限制的背景,并且我们还需要确定很细粒度的关节点坐标。CNN作为很强的图像处理模型,在这一领域表现优异。目前现有的工作通常聚焦于设计针对人体姿态预测的CNN框架。
和图像分类任务中用于表示目标类别标签的one-hot向量一样,人体姿态估计模型(基于CNN)也需要一个用于表示人体关节点坐标的label representation,以方便训练和推理。常用的标准的label representation是coordinate heatmap,生成以每个关节点为中心的二维高斯分布。这些是从coordinate encoding过程得到的,即从coordinate到heatmap。heatmap为ground-truth位置提供空间支持(spatial support),其不但考虑了上下文,并且还考虑了目标位置的模糊性(个人理解:即heatmap不是单纯的只标记一个点,而是一片最有可能的区域)。这可以有效降低模型的过拟合风险。目前SOTA的pose model都使用了heatmap。
对于heatmap label representation,一个弊端就是其计算成本是输入图像分辨率的二次函数,这使得CNN模型无法处理高分辨率的原始图像(个人理解:高分辨率的原始图像会导致计算成本过高)。为了降低计算成本,通常的做法是通过图像预处理将人单独裁剪出来(并且需要resize到一样的固定尺寸)作为模型的输入(见Fig1)。为了获得原始分辨率下的关节点坐标,我们还需要将heatmap预测的坐标还原到原始的坐标空间。最终的预测位置通常在heatmap中具有最大的激活值。我们把从heatmap中提取关节点坐标的过程称为coordinate decoding。但是需要注意的是,在预处理模型输入的时候(从高分辨率到低分辨率)可能会引入量化误差(quantisation error)。为了缓解这个问题,在现有的coordinate decoding过程中,通常会将预测位置从最大激活值向第二大激活值做一个位移(后文称这种方法为Standard Shifting)。
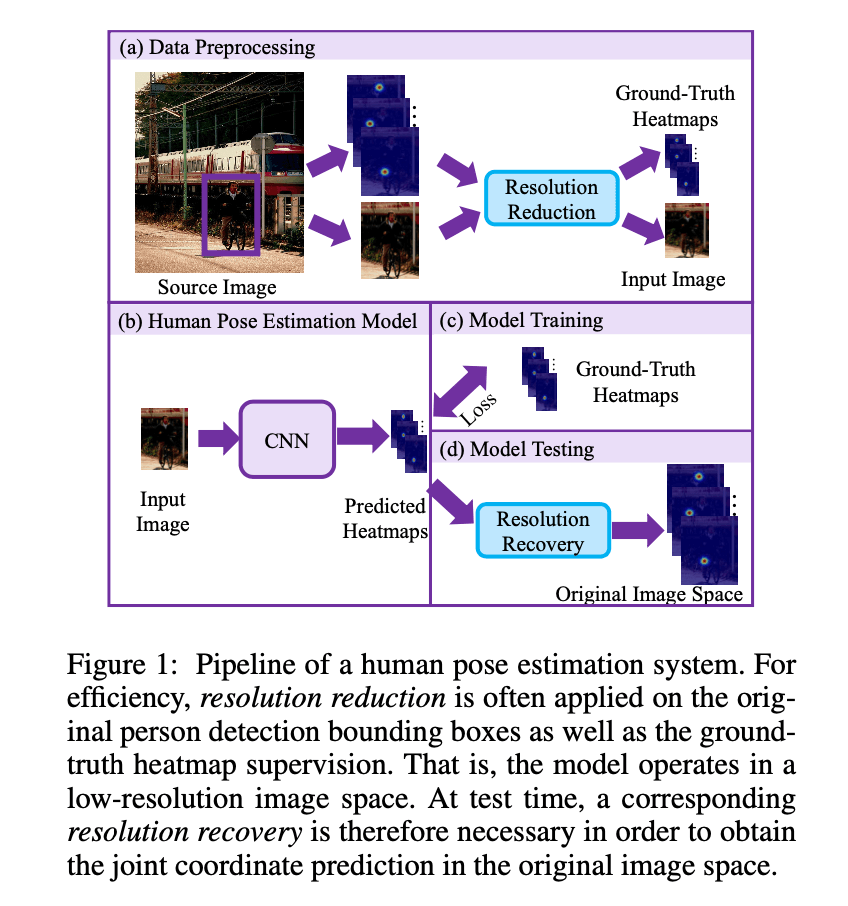
Fig1展示了人体姿态估计系统的pipeline。为了提高效率,通常会对裁剪的人物图像以及对应的ground-truth heatmap进行下采样,即降低分辨率。因此,模型直接处理低分辨率图像。在推理阶段,关节点坐标会被恢复至原始图像分辨率(resolution recovery)。
尽管coordinate的encoding和decoding是模型中不可或缺的一部分,但其却很少受到重视。与目前大多研究都聚焦于设计更有效的CNN结构不同,我们揭示了coordinate representation在模型中的重要性远超预期。例如,SOTA的模型HRNet-W32在使用了Standard Shifting之后,其在COCO验证集上的AP提升了5.7%(见表1)。这种程度的性能提升已经远优于其他的一些先进优化方法。但是据我们所知,这一点从未在其他文献中得到过重视和仔细研究。
因此与现有的人体姿态估计研究不同,我们致力于研究关节点坐标的encoding和decoding。此外,我们还发现heatmap的分辨率是模型使用更小的输入分辨率以进行更快推理的一个主要障碍。使用HRNet-W32模型,当输入分辨率从$256 \times 192$降低到$128 \times 96$时,其在COCO验证集上的性能从74.4%降低到66.9%,尽管计算量从$7.1 \times 10^9$ FLOPs降至$1.8 \times 10^9$ FLOPs。
我们对coordinate representation进行了深入研究,发现了coordinate decoding过程中的一个关键限制。虽然Standard Shifting已经取得了不错的效果,我们提出的基于分布感知的表示方式(distribution-aware representation)可以更精确的定位关节点位置(sub-pixel accuracy)。具体来说,就是用泰勒展开来近似heatmap的分布信息。此外,我们发现标准方法生成ground-truth heatmap时存在量化误差,从而会影响到模型的训练和预测性能。为了解决这个问题,我们提出以sub-pixel位置为中心,通过高斯核(Gaussian kernel)生成无偏(unbiased)的heatmap。
本研究的贡献在于:1)揭示了在人体姿态估计中coordinate representation的重要性,这是之前未被重视的;2)提出新方法:Distribution-Aware coordinate Representation of Keypoint(简称DARK)。DARK主要包含两部分:1)基于coordinate decoding的泰勒展开;2)coordinate encoding阶段的无偏heatmap。此外,DARK可以很容易的嵌入到现有的人体姿态估计算法中。我们将DARK应用于目前SOTA的两个人体姿态估计模型,使其在COCO和MPII上都得到了显著的性能提升。DARK使得我们在使用低分辨率作为模型输入时,性能不会损失太多,同时极大提升了推理效率。
2.Related Work
在人体姿态估计中,有两种常见的coordinate representation设计:direct coordinate和heatmap。两者都用作模型训练的回归目标。
👉Coordinate regression
这种设计直接将坐标作为模型的输出目标。但目前只有极少数的方法采用这种设计。一个可能的原因是,这种设计缺乏空间和上下文信息,使得人体姿态模型的训练极为困难。
👉Heatmap regression
heatmap的设计巧妙的解决了上述限制。其首次提出是在论文“Tompson,J.J.; Jain,A.; LeCun,Y.; and Bregler, C. 2014. Joint training of a convolutional network and a graphical model for human pose estimation. In Advances in Neural Information Processing Systems.”中,并迅速成为最常用的坐标表示方法。目前主流的研究都聚焦于设计网络结构以更有效的训练heatmap。
与之前的研究不同,我们的工作聚焦于heatmap的表示,这点通常被其他研究所忽视。我们不仅揭示了使用heatmap时因降低分辨率而造成的巨大影响,同时也提出了一种新的坐标表示方法,极大的提升了现有模型的性能。重要的是,我们的方法可以无缝集成到已有的其他方法中,而不需要更改之前的模型设计。
3.Methodology
我们认为在人体姿态估计中,坐标表示(coordinate representation)包括encoding和decoding两部分。人体姿态估计的目标是从输入图像中预测出关节点的坐标。在模型的训练和推理阶段,通常都使用heatmap作为坐标表示。在训练阶段,我们将关节点坐标的ground-truth转换成heatmap作为模型的训练目标(即encoding)。在推理阶段,我们通常需要将预测的heatmap转换成原始图像分辨率下的坐标(即decoding)。
接下来我们首先介绍解码过程(decoding process),主要聚焦于现有标准方法的局限性以及新方法的改善。接下来,我们会进一步的讨论并解决编码阶段(encoding process)存在的限制。最后,我们展示了我们的方法和现有人体姿态估计模型的集成。
3.1.Coordinate Decoding
我们认为一直被忽视的解码过程是提升人体姿态估计模型的重要因素之一(见表1)。解码过程指的是将预测的heatmap转换成原始图像分辨率下的关节点坐标。如果heatmap的大小和原始图像的分辨率一样,那么我们直接找到最大激活值的位置即可作为关节点的坐标,这很简单。但实际情况通常不是如此。相反,我们通常需要将heatmap上采样至原始图像分辨率。这就涉及亚像素定位(sub-pixel localisation)的问题。在介绍我们的方法之前,我们先回顾下现有人体姿态估计模型中所用的标准的坐标解码方法。
3.1.1.The standard coordinate decoding method
出自论文:Newell,A.;Yang,K.;and Deng,J. 2016. Stacked hourglass networks for human pose estimation. In European Conference on Computer Vision.。
给定已经训练好的模型预测得到的heatmap $\mathbf{h}$,我们找到$\mathbf{h}$中最大激活值的坐标$\mathbf{m}$和第二大激活值的坐标$\mathbf{s}$。则关节点坐标可被预测为:
\[\mathbf{p} = \mathbf{m} + 0.25 \frac{\mathbf{s}-\mathbf{m}}{\parallel \mathbf{s}-\mathbf{m} \parallel _2} \tag{1}\]即在heatmap分辨率下,预测结果从最大激活值处向第二大激活值的位置移动了(shifting)0.25个像素(即sub-pixel)。将坐标还原到原始图像分辨率下:
\[\hat{\mathbf{p}} = \lambda \mathbf{p} \tag{2}\]$\lambda$为下采样比例(resolution reduction ratio)。
👉Remarks
公式(1)中的sub-pixel shifting是为了补偿图像分辨率下采样而导致的量化效应(quantisation effect)。也就是说,预测得到的heatmap中最大激活值的位置并不对应原始图像分辨率下的精确的关节点坐标,而只是一个粗略的位置。这种shifting带来了显著的性能提升(见表1)。这也在一定程度上解释了为什么这种方法会被视为一种标准操作。但是据我们所知,还没有具体的工作深入研究这种shifting操作对人体姿态估计模型的性能影响。因此,它的真正意义从未在文献中得到真正的承认和报道。这种标准方法缺少直观性和可解释性,并且没有进一步的被改进。而我们则填补了这一空白。
3.1.2.The proposed coordinate decoding method
我们提出的方法会探索heatmap的分布结构,以推断出潜在的最大激活值。这与标准方法有很大的不同,因为标准方法的offset是人为设定的,几乎没有什么设计原理。
为了获得sub-pixel级别的精确位置,我们假设预测得到的heatmap和ground-truth heatmap都服从二维高斯分布。因此,我们将预测得到的heatmap表示为:
\[\mathcal{G} (\mathbf{x}; \mathbf{\mu}, \Sigma) = \frac{1}{(2\pi) \lvert \Sigma \rvert^{\frac{1}{2}}} exp \left( -\frac{1}{2} (\mathbf{x}-\mathbf{\mu})^T \Sigma^{-1} (\mathbf{x} - \mathbf{\mu}) \right) \tag{3}\]$\mathbf{x}$为预测的heatmap中的像素坐标,均值$\mathbf{\mu}$可理解为被预测的目标关节点的坐标。协方差矩阵$\Sigma$为对角矩阵:
\[\Sigma = \begin{bmatrix} \sigma^2 & 0 \\ 0 & \sigma^2 \\ \end{bmatrix} \tag{4}\]$\sigma$为标准差,两个方向(即x方向和y方向)的标准差是一样的。
取对数,既方便计算,也不会改变最大激活值的位置:
\[\mathcal{P} (\mathbf{x}; \mathbf{\mu}, \Sigma) = \ln (\mathcal{G}) = -\ln (2\pi) - \frac{1}{2} \ln (\lvert \Sigma \rvert) - \frac{1}{2} (\mathbf{x} - \mathbf{\mu})^T \Sigma^{-1} (\mathbf{x} - \mathbf{\mu}) \tag{5}\]我们的目的是得到$\mathbf{\mu}$。$\mathbf{\mu}$作为高斯分布的极值点,其一阶导数为0:
\[\mathcal{D}'(\mathbf{x}) \big| _{\mathbf{x}=\mathbf{\mu}} = \frac{\partial \mathcal{P}^T}{\partial \mathbf{x}} \big| _{\mathbf{x}=\mathbf{\mu}} = -\Sigma ^{-1} (\mathbf{x} - \mathbf{\mu}) \big| _{\mathbf{x}=\mathbf{\mu}} = 0 \tag{6}\]使用二阶泰勒展开来近似$\mathbf{m}$附近的函数值:
\[\mathcal{P} (\mathbf{\mu}) = \mathcal{P}(\mathbf{m}) + \mathcal{D}' (\mathbf{m}) (\mathbf{\mu}-\mathbf{m})+\frac{1}{2} (\mathbf{\mu}-\mathbf{m})^T \mathcal{D}''(\mathbf{m}) (\mathbf{\mu}-\mathbf{m}) \tag{7}\]其中,$\mathcal{D}’‘$为$\mathcal{P}$在点$\mathbf{m}$处的二阶导数(即Hessian矩阵),正式定义为:
\[\mathcal{D}'' (\mathbf{m}) = \mathcal{D}'' (\mathbf{x}) \big| _{\mathbf{x} = \mathbf{m}} = -\Sigma^{-1} \tag{8}\]结合式(6),(7),(8)可得:
\[\mathbf{\mu} = \mathbf{m} - (\mathcal{D}''(\mathbf{m}))^{-1} \mathcal{D}' (\mathbf{x}) \tag{9}\]其中$\mathcal{D}’‘$和$\mathcal{D}’$可以很容易从heatmap中计算得到。一旦得到了$\mathbf{\mu}$,我们就可以应用式(2)将坐标还原至原始分辨率下。
个人理解:说了这么多,其实就是用了牛顿法,相当于是只迭代了一次。
👉Remarks
与标准方法中仅考虑第二大激活值不同,我们提出的方法充分考虑了heatmap的分布统计,以更准确的揭示潜在的最大值。在原理上,我们假设heatmap服从高斯分布。更重要的是,我们的方法很有计算效率,因为只需计算每个heatmap中一个位置的一阶导数和二阶导数。因此,即使我们的方法嵌入到现有的人体姿态估计模型中,也不会增加过多的计算成本。
3.1.3.Heatmap distribution modulation
因为我们的方法基于高斯分布的假设,所以我们有必要检查该假设的满足程度。我们发现,与训练的heatmap(个人理解:即ground-truth heatmap)相比,预测得到的heatmap通常不能呈现出一个良好的高斯分布结构。如Fig3所示,预测的heatmap在最大激活值附近常呈多峰分布。这可能会对我们的方法造成不好的影响。为了解决这个问题,我们建议预先修改heatmap分布。
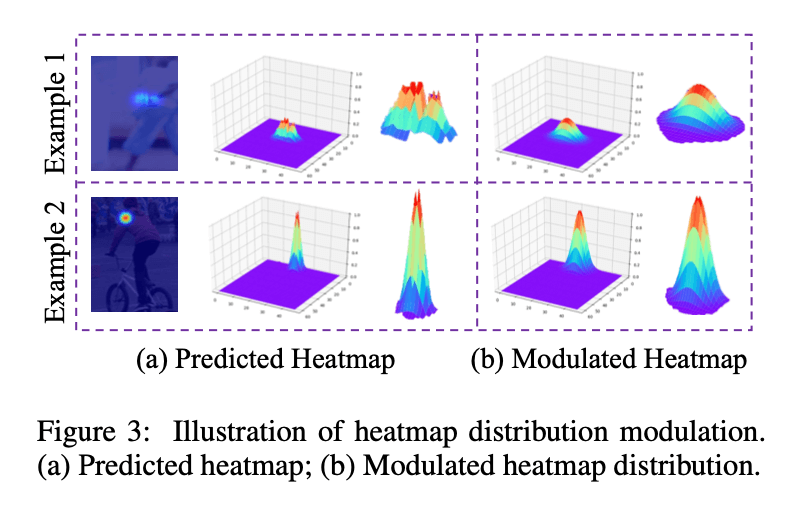
Fig3中,(a)为预测得到的heatmap分布,(b)为修改后的heatmap分布。
修改的具体实现方式为使用和训练过程中一样的高斯核$K$来平滑heatmap的多峰分布,即:
\[\mathbf{h}' = K \circledast \mathbf{h} \tag{10}\]$\circledast$表示卷积操作。
为了保持原有heatmap的magnitude,我们对$\mathbf{h}’$进行scale操作以保证最大激活值和$\mathbf{h}$的一致性:
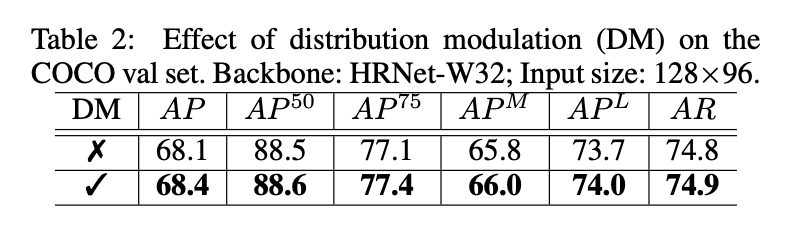
\[\mathbf{h}' = \frac{\mathbf{h}' - \min (\mathbf{h}')}{\max (\mathbf{h}') - \min (\mathbf{h}')} * \max (\mathbf{h}) \tag{11}\]其中$\max()$和$\min()$分别返回输入矩阵的最大和最小值。我们的实验证明这种分布调整策略(distribution modulation)进一步提升了我们方法的性能表现(见表3),其视觉效果和定性评估见Fig3(b)。
3.1.4.Summary
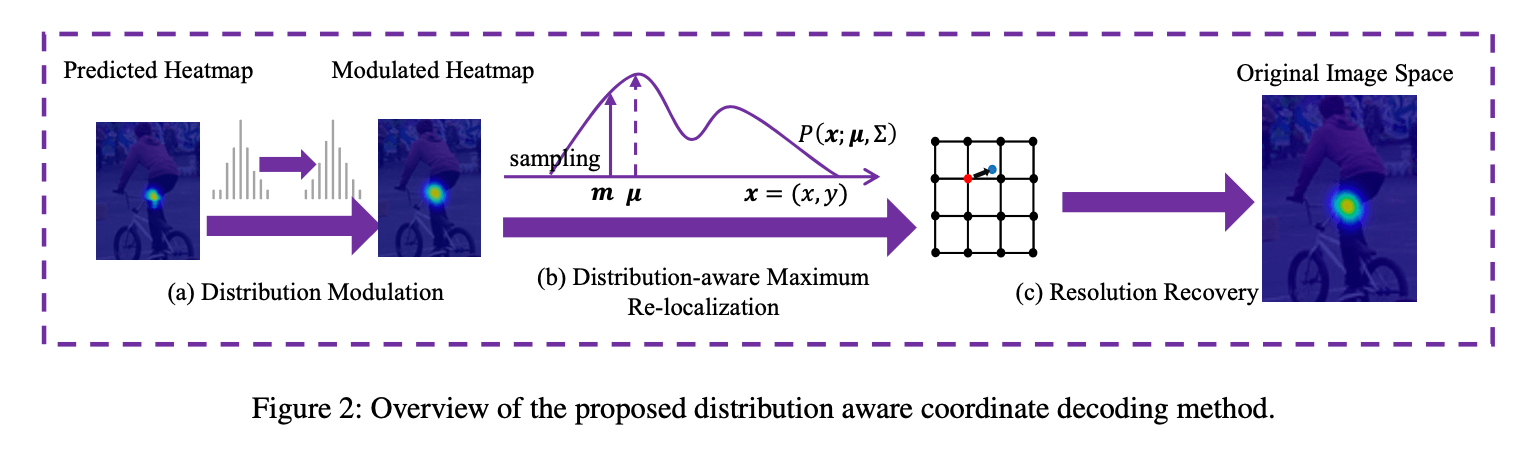
我们把我们提出的坐标解码方法归纳为Fig2。具体来说,总的流程包括三步:
- Heatmap distribution modulation(见式(10),(11))
- 通过泰勒展开,基于分布感知,在亚像素水平上实现关节点的精准定位(见式(3)-(9))
- 将关节点坐标恢复至原始分辨率下(见式(2))
这些步骤都不会产生很高的计算成本,因此可以高效的嵌入现有其他模型中。
3.2.Coordinate Encoding
标准的坐标编码方法首先将原始人物图像降采样为模型输入大小。因此,在生成heatmap之前,需要将关节点坐标的ground-truth进行变换。
我们用$\mathbf{g} = (u,v)$表示关节点坐标的ground-truth。分辨率降低(resolution reduction)后变换得到的关节点坐标为:
\[\mathbf{g}' = (u',v') = \frac{\mathbf{g}}{\lambda} = (\frac{u}{\lambda},\frac{v}{\lambda}) \tag{12}\]$\lambda$为下采样比例。
为了后续使用方便,$\mathbf{g}’$通常会被取整(quantise),得到$\mathbf{g}’’$:
\[\mathbf{g}'' = (u'',v'') = \text{quantise} (\mathbf{g}') = \text{quantise} (\frac{u}{\lambda},\frac{v}{\lambda}) \tag{13}\]取整操作($\text{quantise} ()$)可以是向下取整(floor),向上取整(ceil)或四舍五入取整(round)。
随后便以$\mathbf{g}’‘$为中心生成符合二维高斯分布的heatmap:
\[\mathcal{G} (x,y;\mathbf{g}'')=\frac{1}{2\pi \sigma^2} exp \left( -\frac{(x-\mu '')^2 + (y-v'')^2}{2\sigma^2} \right) \tag{14}\]$(x,y)$为heatmap中某一像素点的坐标。
显然,因为取整操作导致的量化误差(quantisation error),使其生成的heatmap是不准确且有偏差的(inaccurate and biased)(见Fig4)。这有可能导致模型学习的目标本身就是有偏差的,从而导致模型性能下降。

Fig4阐述了标准坐标编码过程中的量化误差。图中蓝色的点表示准确的关节点坐标(即$\mathbf{g}’$)。如果采用向下取整的策略,则红色的箭头就代表了量化误差。其他的量化方法也存在同样的问题。
为了解决量化误差这个问题,我们采用准确的$\mathbf{g}’$作为中心生成符合二维高斯分布的heatmap(即unbiased heatmap)。公式依然采用式(14),只不过是把$\mathbf{g}’‘$换成了$\mathbf{g}’$。我们在后文展示了使用unbiased heatmap的好处(见表3)。
3.3.Integration with State-of-the-Art Models
我们的DARK方法与模型无关,可以和任何现有基于heatmap的pose模型无缝集成。重要的是,基本不需要对以前算法进行太多更改。在训练阶段,唯一的更改就是ground-truth heatmap的生成会基于更准确的关节点坐标。在推理阶段,DARK使用预测的heatmap作为输入,输出在原始分辨率下的更准确的关节点坐标。在整个生命周期中,我们尽可能保持原有模型的设计不变。这使得我们的方法有着很强的通用性和可扩展性。
4.Experiments
👉Datasets
我们使用了两个常见的人体姿态估计数据集,COCO和MPII。
- COCO keypoint数据集包含不同的人体姿态、各种背景环境、不同大小的人和不同的遮挡模式。整个目标包括人物实例(person instance)和关节点位置。一共包含200,000张图像,250,000个人物实例。每个人物实例标记17个关节点。训练集和验证集的标注是公开的。在评估时,使用常用的train2017/val2017/test-dev2017的数据集划分方式。
- MPII人体姿态数据集包含40k个人物实例,每个人物实例标记16个关节点。训练集,验证集,测试集的划分遵循论文“Tompson,J.J.; Jain,A.; LeCun,Y.; and Bregler, C. 2014. Joint training of a convolutional network and a graphical model for human pose estimation. In Advances in Neural Information Processing Systems.”。
👉Evaluation metrics
对于COCO数据集,我们使用Object Keypoint Similarity(OKS)作为模型性能评估指标。对于MPII数据集,我们使用Percentage of Correct Keypoints(PCK)作为模型性能评估指标。
👉Implementation details
针对模型训练,使用Adam优化算法。对于HRNet和Simple-Baseline,我们使用和原文一样的learning schedule和epochs。对于Hourglass模型,初始学习率调整为2.5e-4,在第90个epoch时降低至2.5e-5,在第120个epoch时降低至2.5e-6。一共执行140个epoch。在我们的实验中,使用了3种不同的input size($128 \times 96$,$256 \times 192$,$384 \times 288$)。数据预处理方法和HRNet原文保持一致。
Simple-Baseline原文:Xiao, B.; Wu, H.; and Wei, Y. 2018. Simple baselines for human pose estimation and tracking. In European Conference on Computer Vision.。
Hourglass原文:Newell,A.; Yang,K.; and Deng,J. 2016. Stacked hourglass networks for human pose estimation. In European Conference on Computer Vision.。
4.1.Evaluating Coordinate Representation
作为这项工作的核心问题,首先研究了coordinate representation对模型性能的影响,以及其和输入图像分辨率之间的关系。在这项测试中,默认使用HRNet-W32作为backbone,input size为$128 \times 96$,在COCO验证集上进行测试。
4.1.1.Coordinate decoding
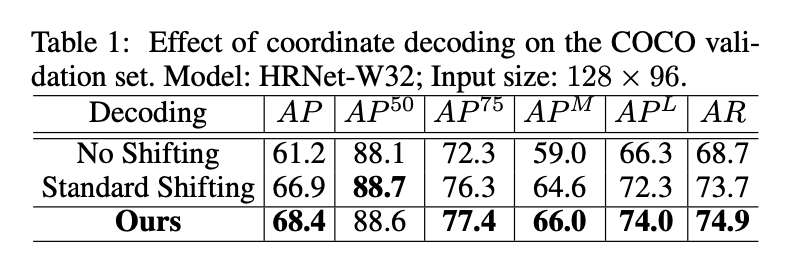
我们评估了坐标解码的效果,特别是shifting操作(即标准解码方法)和distribution modulation(即作者提出的方法)。使用常规的biased heatmap。我们首先比较了两种方法:1)无shifting操作,直接使用最大激活值;2)标准解码方法,即shifting操作(即式(1))。我们从表1中有两个重要发现:
- 相比无shifting操作,标准解码方法将AP提升了5.7%,效果非常好。据我们所知,这是文献中首次报道的有效性分析,因为这一问题在很大程度上被以前的研究所忽视。这揭示了先前未发现的坐标解码过程对人体姿态估计的重要性。
- 尽管标准解码方法将性能提升了很多,但是我们的方法将AP在此基础上又提高了1.5%。这1.5%中有0.3%的提升来自distribution modulation,见表2。这验证了我们提出的解码方法的优越性。
4.1.2.Coordinate encoding
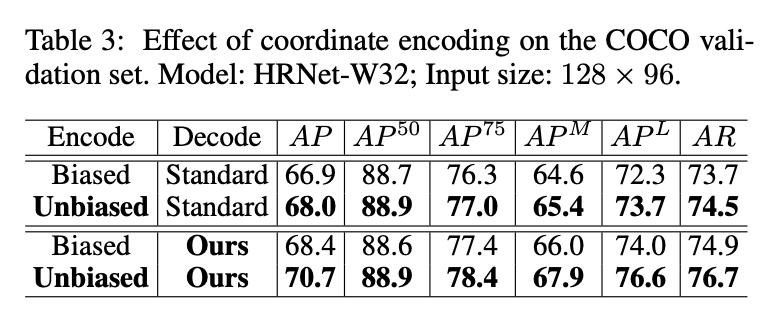
我们也测试了坐标编码的有效性。我们比较了我们提出的unbiased encoding和standard biased encoding分别搭配standard decoding和我们提出的decoding方法的效果。结果见表3,我们发现无论是哪种解码方法,unbiased encoding总能带来性能上的提升(AP值的提升都大于1%)。这表明了坐标编码的重要性,而以前的研究也忽视了这一点。
4.1.3.Input resolution
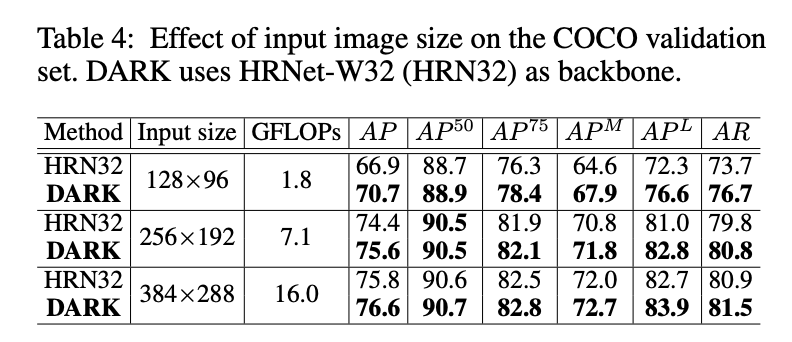
考虑到输入图像的分辨率/大小是影响模型推理效率的一个重要因素,因此我们测试了不同输入图像大小。我们比较了我们的DARK模型(使用HRNet-W32作为backbone)和原始的HRNet-W32模型(训练阶段使用的是biased heatmap,推理阶段使用的是standard shifting)。从表4中我们有以下发现:
- 正如预期的那样,随着输入图像尺寸的减小,模型性能不断下降,但是其推理成本也在明显下降。
- 在DARK的加持下,可以有效减轻模型性能的损失,特别是在输入分辨率非常小的时候。这有助于在低资源设备上部署人体姿态估计模型。
4.1.4.Generality
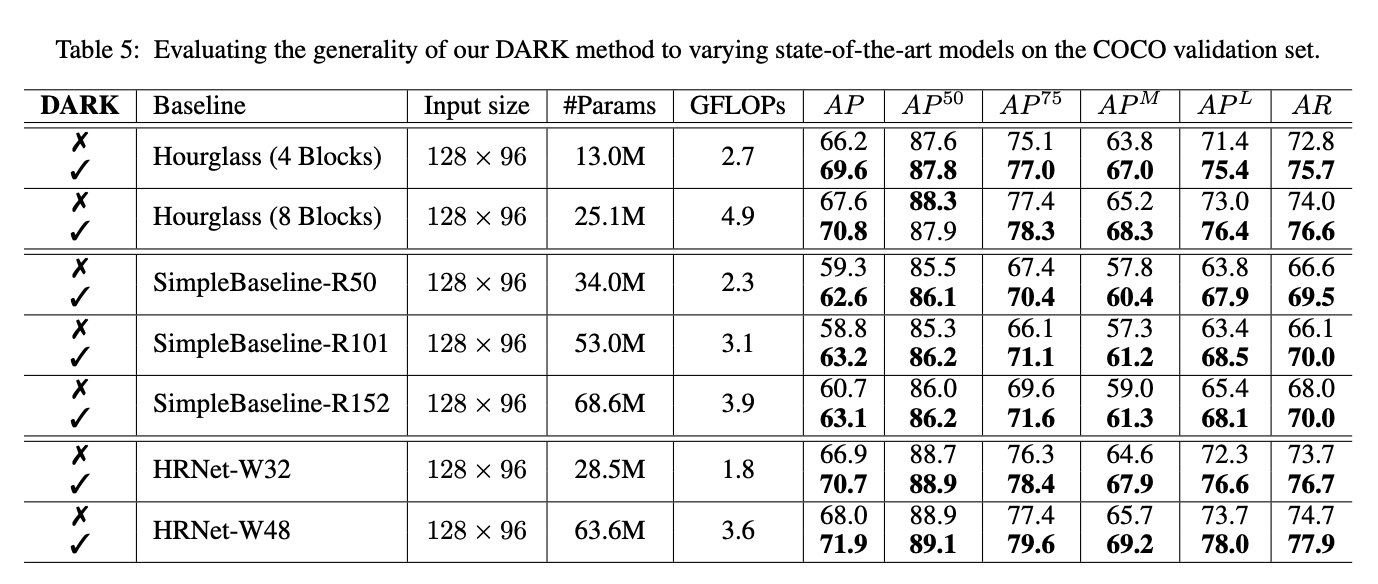
除了SOTA的HRNet,我们还测试了另外两个具有代表性的人体姿态估计模型:SimpleBaseline和Hourglass。表5的结果表明,在大多数情况下,DARK为现有模型提供了显著的性能提升。这也表明我们的方法具有普遍的实用性。定性评估(qualitative evaluation)见Fig5。

4.1.5.Complexity
我们测试了DARK方法(HRNet-W32为backbone,输入大小为$128\times 96$)的推理效率。在Titan V GPU上,运行速度从360fps降低至320fps,降低了大约11%。我们认为这是完全可以接受的。
4.2.Comparison to the State-of-the-Art Methods
4.2.1.Evaluation on COCO
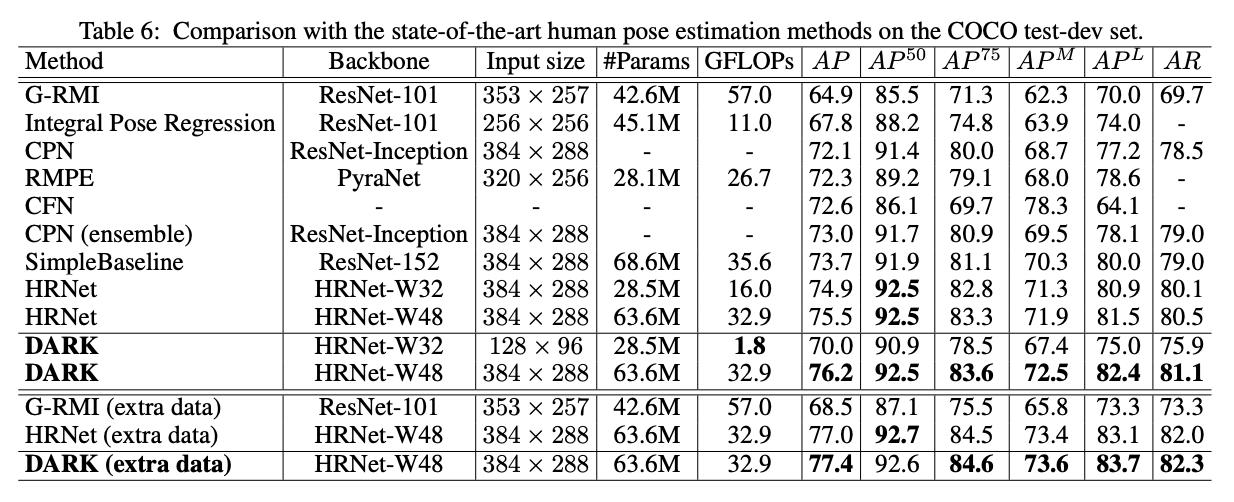
我们将DARK方法和表现前几的方法进行了比较,这些方法有G-RMI,Integral Pose Regression,CPN,RMPE,SimpleBaseline和HRNet。表6展示了这些方法在COCO test-dev数据集上的表现。我们有以下发现:
- 基于HRNet-W48且输入大小为$384 \times 288$的DARK模型准确率是最高的,并且计算成本只增加了一点点。尤其是和最强劲的对手(HRNet-W48,输入大小也为$384 \times 288$)比较时,DARK将AP提升了0.7%(76.2-75.5)。当和最有效率的模型(Integral Pose Regression,即GFLOPs最低)比较时,DARK(基于HRNet-W32)将AP提升了2.2%(70.0-67.8),但计算成本只有原来的16.4%(1.8/11.0 GFLOPs)。这些都表明了DARK在准确性和效率方面优于现有模型。
G-RMI原文:Papandreou, G.; Zhu, T.; Kanazawa, N.; Toshev, A.; Tompson, J.; Bregler, C.; and Murphy, K. 2017. Towards accurate multi-person pose estimation in the wild. In IEEE Conference on Computer Vision and Pattern Recognition, 4903– 4911.。
Integral Pose Regression原文:Sun, X.; Xiao, B.; Wei, F.; Liang, S.; and Wei, Y. 2018. Integral human pose regression. In European Conference on Computer Vision.。
CPN原文:Chen,Y.; Wang,Z.; Peng,Y.; Zhang,Z.; Yu,G.; and Sun, J. 2018. Cascaded pyramid network for multi-person pose estimation. In IEEE Conference on Computer Vision and Pattern Recognition.。
RMPE原文:Fang, H.-S.; Xie, S.; Tai, Y.-W.; and Lu, C. 2017. Rmpe: Regional multi-person pose estimation. In IEEE Conference on Computer Vision and Pattern Recognition, 2334–2343.。
4.2.2.Evaluation on MPII

我们在MPII验证集上比较了DARK和HRNet-W32。表7中的结果表明我们的方法通常表现更为优异。在更严格的PCKh@0.1指标下,DARK的提升幅度更大。并且,MPII的训练集比COCO小的多,这说明我们的方法适用于不同大小的训练集。
5.Conclusion
在这项工作中,我们首次系统地研究了在人体姿态估计任务中,之前被广泛忽视的重要问题:coordinate representation(包含encoding和decoding)。我们不仅揭示了这个问题的真正意义,还提出了DARK方法。现有的SOTA的模型可以无缝集成DARK以获得收益且不需要增加过多的计算成本。我们还在两个具有挑战性的数据集上验证了DARK的性能优势。
6.原文链接
👽Distribution-Aware Coordinate Representation for Human Pose Estimation