【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.核化线性降维
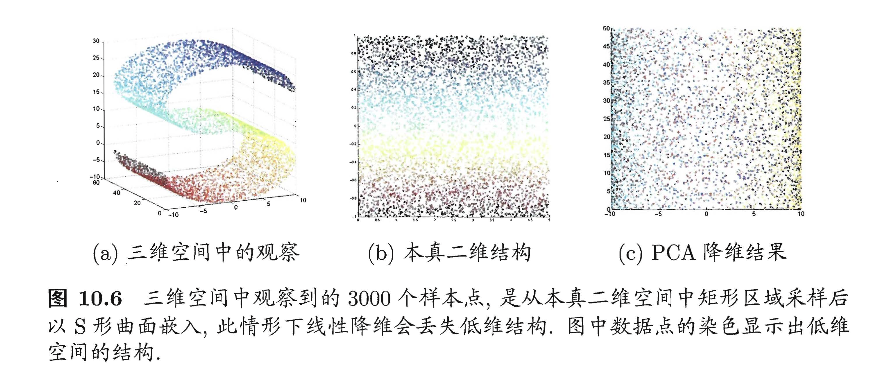
线性降维方法假设从高维空间到低维空间的函数映射是线性的,然而,在不少现实任务中,可能需要非线性映射才能找到恰当的低维嵌入。图10.6给出了一个例子,样本点从二维空间中的矩形区域采样后以S形曲面嵌入到三维空间,若直接使用线性降维方法对三维空间观察到的样本点进行降维,则将丢失原本的低维结构。为了对“原本采样的”低维空间与降维后的低维空间加以区别,我们称前者为“本真”(intrinsic)低维空间。
数据分布不是线性的,当初SVM也遇到了这个问题,其解决办法为把数据映射到高维空间,在高维空间这些数据就是线性的了,然后我们就可以用上只能处理线性分布数据的PCA来进行降维了。这套思路其实就是核主成分分析(Kernelized PCA,简称KPCA)。KPCA是非线性降维的一种常用方法,是基于核技巧对线性降维方法进行“核化”(kernelized)。
假定我们将在高维特征空间中把数据投影到由$\mathbf{W}$确定的超平面上,即PCA欲求解:
\[\left( \sum_{i=1}^m \mathbf{z}_i \mathbf{z}_i^T \right) \mathbf{W} = \lambda \mathbf{W} \tag{1}\]其中$\mathbf{z}_i$是样本点$\mathbf{x}_i$在高维特征空间中的像。易知:
\[\begin{align} \mathbf{W} &= \frac{1}{\lambda} \left( \sum_{i=1}^m \mathbf{z}_i \mathbf{z}_i^T \right) \mathbf{W} \\&= \sum_{i=1}^m \mathbf{z}_i \frac{\mathbf{z}_i^T \mathbf{W}}{\lambda} \\&= \sum_{i=1}^m \mathbf{z}_i \mathbf{\alpha}_i \end{align} \tag{2}\]其中$\mathbf{\alpha}_i = \frac{1}{\lambda} \mathbf{z}_i^T \mathbf{W}$。假定$\mathbf{z}_i$是由原始属性空间中的样本点$\mathbf{x}_i$通过映射$\phi$产生,即$\mathbf{z}_i = \phi (\mathbf{x}_i),i=1,2,…,m$。若$\phi$能被显式表达出来,则通过它将样本映射至高维特征空间,再在(高维)特征空间中实施PCA即可。式(1)变换为:
\[\left( \sum_{i=1}^m \phi(\mathbf{x}_i) \phi(\mathbf{x}_i)^T \right) \mathbf{W} = \lambda \mathbf{W} \tag{3}\]式(2)变换为:
\[\mathbf{W} = \sum_{i=1}^m \phi (\mathbf{x}_i) \mathbf{\alpha_i} \tag{4}\]一般情形下,我们不清楚$\phi$的具体形式,于是引入核函数:
\[\kappa (\mathbf{x}_i, \mathbf{x}_j) = \phi (\mathbf{x}_i)^T \phi (\mathbf{x}_j) \tag{5}\]将式(4)和(5)代入式(3)后化简。先看式(3)的左侧:
\[\begin{align} \left( \sum_{i=1}^m \phi(\mathbf{x}_i) \phi(\mathbf{x}_i)^T \right) \mathbf{W} &= \left( \sum_{i=1}^m \phi(\mathbf{x}_i) \phi(\mathbf{x}_i)^T \right) \sum_{j=1}^m \phi (\mathbf{x}_j) \mathbf{\alpha_j} \\&= \left(\phi(\mathbf{x}_1) \phi(\mathbf{x}_1)^T + \phi(\mathbf{x}_2) \phi(\mathbf{x}_2)^T + ... + \phi(\mathbf{x}_m) \phi(\mathbf{x}_m)^T \right) \left( \phi(\mathbf{x}_1)\mathbf{\alpha_1} + \phi(\mathbf{x}_2)\mathbf{\alpha_2} + ... + \phi(\mathbf{x}_m)\mathbf{\alpha_m} \right) \\&= \left(\phi(\mathbf{x}_1) \kappa(\mathbf{x}_1,\mathbf{x}_1) + \phi(\mathbf{x}_2) \kappa(\mathbf{x}_2,\mathbf{x}_1) + ... + \phi(\mathbf{x}_m) \kappa(\mathbf{x}_m,\mathbf{x}_1) \right) \mathbf{\alpha}_1 + \\& \quad \left(\phi(\mathbf{x}_1) \kappa(\mathbf{x}_1,\mathbf{x}_2) + \phi(\mathbf{x}_2) \kappa(\mathbf{x}_2,\mathbf{x}_2) + ... + \phi(\mathbf{x}_m) \kappa(\mathbf{x}_m,\mathbf{x}_2) \right) \mathbf{\alpha}_2 + \\& \quad ... \\& \quad \left(\phi(\mathbf{x}_1) \kappa(\mathbf{x}_1,\mathbf{x}_m) + \phi(\mathbf{x}_2) \kappa(\mathbf{x}_2,\mathbf{x}_m) + ... + \phi(\mathbf{x}_m) \kappa(\mathbf{x}_m,\mathbf{x}_m) \right) \mathbf{\alpha}_m \\& = \phi(\mathbf{x}_1) \left( \kappa(\mathbf{x}_1,\mathbf{x}_1) \mathbf{\alpha}_1 + \kappa(\mathbf{x}_1,\mathbf{x}_2) \mathbf{\alpha}_2 + ... + \kappa(\mathbf{x}_1,\mathbf{x}_m) \mathbf{\alpha}_m \right) + \\& \quad \phi(\mathbf{x}_2) \left( \kappa(\mathbf{x}_2,\mathbf{x}_1) \mathbf{\alpha}_1 + \kappa(\mathbf{x}_2,\mathbf{x}_2) \mathbf{\alpha}_2 + ... + \kappa(\mathbf{x}_2,\mathbf{x}_m) \mathbf{\alpha}_m \right) + \\& \quad ... \\& \quad \phi(\mathbf{x}_m) \left( \kappa(\mathbf{x}_m,\mathbf{x}_1) \mathbf{\alpha}_1 + \kappa(\mathbf{x}_m,\mathbf{x}_2) \mathbf{\alpha}_2 + ... + \kappa(\mathbf{x}_m,\mathbf{x}_m) \mathbf{\alpha}_m \right) \\&= \begin{bmatrix} \phi(\mathbf{x}_1) & \phi(\mathbf{x}_2) & \cdots & \phi(\mathbf{x}_m) \end{bmatrix} \begin{bmatrix} \kappa(\mathbf{x}_1,\mathbf{x}_1) & \kappa(\mathbf{x}_1,\mathbf{x}_2) & \cdots & \kappa(\mathbf{x}_1,\mathbf{x}_m) \\ \kappa(\mathbf{x}_2,\mathbf{x}_1) & \kappa(\mathbf{x}_2,\mathbf{x}_2) & \cdots & \kappa(\mathbf{x}_2,\mathbf{x}_m) \\ \vdots & \vdots & \ddots & \vdots \\ \kappa(\mathbf{x}_m,\mathbf{x}_1) & \kappa(\mathbf{x}_m,\mathbf{x}_2) & \cdots & \kappa(\mathbf{x}_m,\mathbf{x}_m) \end{bmatrix} \begin{bmatrix} \mathbf{\alpha}_1 \\ \mathbf{\alpha}_2 \\ \vdots \\ \mathbf{\alpha}_m \end{bmatrix} \\&= \begin{bmatrix} \phi(\mathbf{x}_1) & \phi(\mathbf{x}_2) & \cdots & \phi(\mathbf{x}_m) \end{bmatrix} \mathbf{K} \mathbf{A} \end{align} \tag{6}\]然后看式(3)的右侧:
\[\begin{align} \lambda \mathbf{W} &= \lambda \sum_{i=1}^m \phi (\mathbf{x}_i) \mathbf{\alpha_i} \\&= \lambda \begin{bmatrix} \phi(\mathbf{x}_1) & \phi(\mathbf{x}_2) & \cdots & \phi(\mathbf{x}_m) \end{bmatrix} \begin{bmatrix} \mathbf{\alpha}_1 \\ \mathbf{\alpha}_2 \\ \vdots \\ \mathbf{\alpha}_m \end{bmatrix} \\&=\begin{bmatrix} \phi(\mathbf{x}_1) & \phi(\mathbf{x}_2) & \cdots & \phi(\mathbf{x}_m) \end{bmatrix} \lambda \mathbf{A} \end{align} \tag{7}\]由于我们的目标是求出$\mathbf{W}$,即等价于求出$\mathbf{A}$使得式(6)等于式(7),显然,如果满足式(8)的话,那么式(6)肯定是等于式(7)的,因此,问题转化为通过式(8)求解$\mathbf{A}$:
\[\mathbf{KA} = \lambda \mathbf{A} \tag{8}\]其中,$\mathbf{K}$为核矩阵。很明显,式(8)是特征值分解问题,取$\mathbf{K}$最大的$d’$个特征值对应的特征向量即可。
对新样本$\mathbf{x}$:
\[\begin{align} \mathbf{z}' &= \mathbf{W}^T \phi(\mathbf{x}) \\&= \sum_{i=1}^m \mathbf{\alpha}_i^T \phi (\mathbf{x}_i)^T \phi(\mathbf{x}) \\&= \sum_{i=1}^m \mathbf{\alpha}_i^T \kappa(\mathbf{x}_i,\mathbf{x}) \end{align} \tag{9}\]从式(9)可以看出,为获得降维后的坐标,KPCA需对所有样本求和,因此它的计算开销较大。