本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.SIFT特征检测原理
SIFT全称为Scale Invariant Feature Transform。SIFT特征在面对图像缩放或者图像旋转时具有不变性,并且在亮度改变和3D视野下,也具有部分的不变性。此外,这一特征对遮挡、杂乱以及噪声有一定的抵抗能力。
1.1.建立高斯差分金字塔
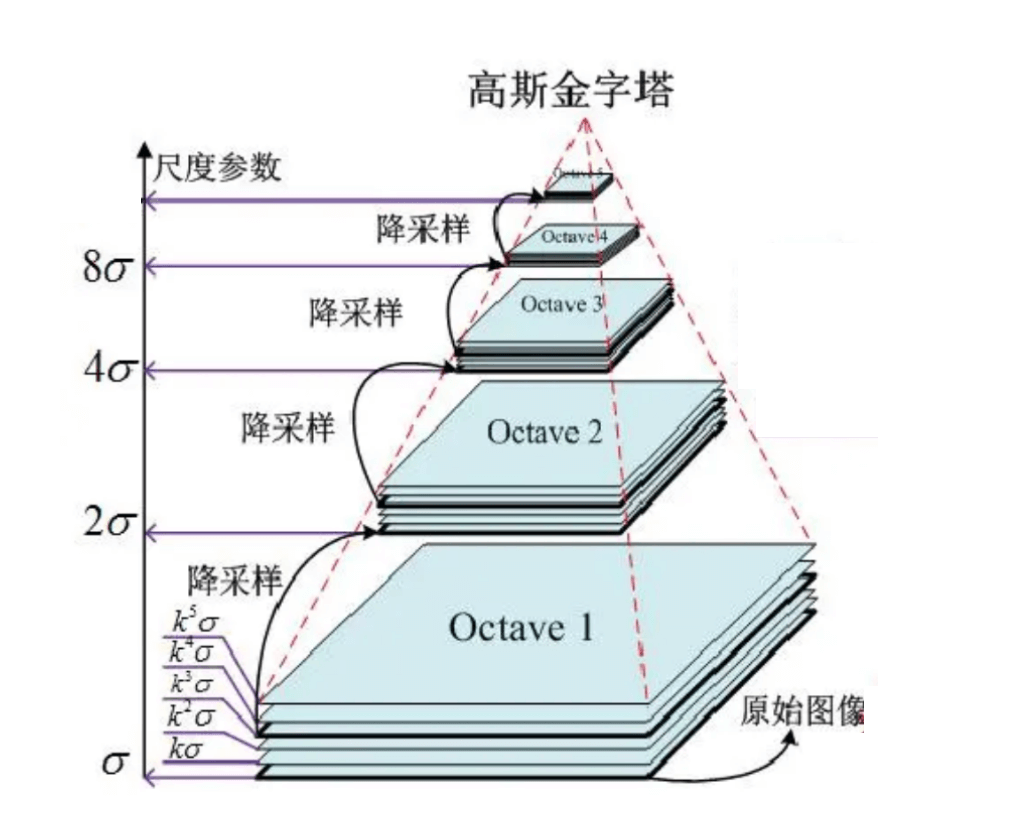
首先建立高斯金字塔,如上图所示,同一octave内图像大小是一样的,从octave1到octave5,图像尺寸逐渐减小,octave2的长和宽分别是octave1的一半,剩余的依此类推。其中,octave1是基于原始图像做不同尺度的高斯模糊。每个octave内都有多层,每层使用不同的$\sigma$值(即不同的尺度)来进行高斯模糊。
接下来我们可以基于高斯金字塔来构建高斯差分金字塔(difference-of-Gaussian,DOG):
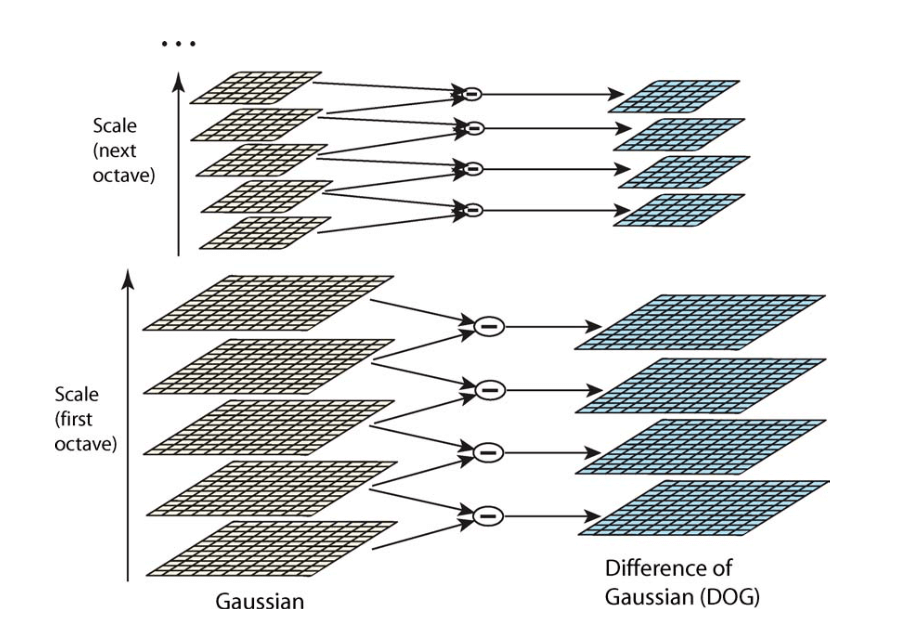
原理也很简单,就是同一octave内相邻两层做减法。
此外,SIFT的作者还给出了一些经验值。octave的个数通常设置为:
\[o = [\log _2 (\min (M,N))] - 3\]其中,$o$为octave的个数,$M,N$为原始图像的长和宽。每个octave内的层数通常设置为:
\[S = n +3\]其中,$S$为每个octave内的层数,$n$表示从$n$幅图像中提取特征。这么计算的原因在于,后续步骤在提取极值点时需要考虑上下两层26邻域内的值,以上图中的高斯差分金字塔为例,对于某个octave,只有中间两层有上下两层,所以有$n=2$,那么在高斯金字塔中,我们就对应需要5层,即$2+3$。
因为我们希望SIFT特征在面对图像缩放时具有不变性,而高斯金字塔刚好就可以很好的模拟近大远小这一概念,并且符合近处清晰、远处模糊的特点,这和现实世界的视角是一致的。此外,高斯核是唯一一个可以模拟近处清晰、远处模糊的线性核,因此我们也不能换用其他卷积核。
在构建高斯金字塔时,每个octave内,不同层的$\sigma$设置见下:

我们令:
\[k = 2 ^{1/n}\]可以看到,我们将octave1的第$n+1$层的$k^n \sigma$,也就是$2\sigma$,用于octave2的起始,后面的依此类推。octave1中第一层所用的$\sigma$设为:
\[\sigma _0 = \sqrt{1.6^2 - 0.5^2} = 1.52\]原因在于,对于完全清晰的图像,作者希望使用$\sigma = 1.6$来进行第一层的高斯模糊,但是相机拍摄的图像通常不是完全清晰的,其自带一些模糊效果,作者给出的这个模糊效果的经验值是$\sigma=0.5$,因此,我们使用$\sigma = 1.52$,再叠加上相机固有的模糊,便可得到预期的$\sigma = 1.6$的效果。
那么DOG中每层的尺度该怎么确定呢?根据原始论文中的描述,一张图像的尺度空间可以定义为一个函数$L(x,y,\sigma)$,该函数由不同尺度(即不同$\sigma$)的高斯函数$G(x,y,\sigma)$与输入图像$I(x,y)$卷积得到:
\[L(x,y,\sigma) = G(x,y,\sigma) * I(x,y)\]$*$表示卷积操作,且有:
\[G(x,y,\sigma) = \frac{1}{2 \pi \sigma^2} e^{-(x^2+y^2)/2\sigma^2}\]DOG的生成我们用函数$D(x,y,\sigma)$来表示,其实就是计算两个相邻尺度的差异(假设相邻尺度差了$k$倍):
\[\begin{align} D(x,y,\sigma) &= (G(x,y,k\sigma)-G(x,y,\sigma)) * I(x,y) \\&= L(x,y,k\sigma) - L(x,y,\sigma) \end{align}\]1.2.关键点的精确定位
1.2.1.阈值化
我们只考虑高斯差分金字塔中绝对值大于$0.5T/n$($T$通常设置为0.04,$n$的含义和1.1部分相同)的点。绝对值小于$0.5T/n$的点通常被认为是噪声。
1.2.2.在高斯差分金字塔中找极值
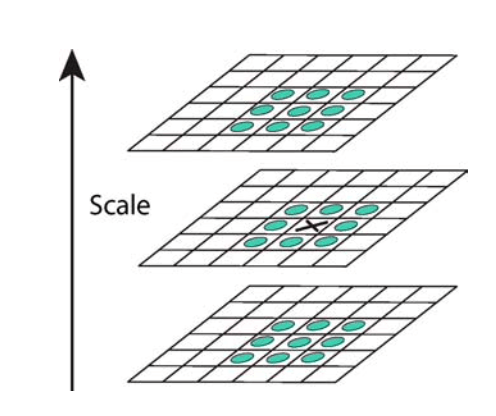
在经过1.2.1部分筛选后的点中进一步寻找极值点,即其在26邻域内是最大值或最小值。
但是这一步是基于离散空间找到的极值点,可能并不是真正的极值点所在的位置:
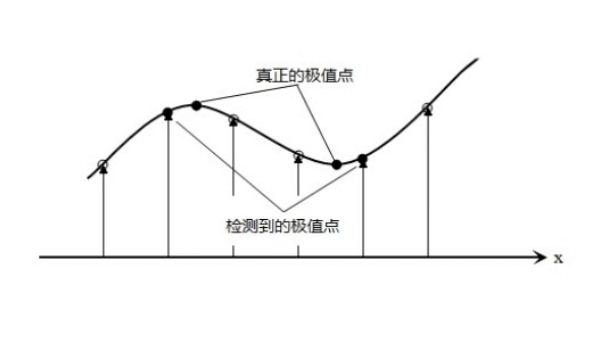
离散空间可以从两方面来理解:
- 就图像的$x,y$方向来说,像素坐标都是整数。
- 从$\sigma$方向来说,就是沿着尺度的方向,相邻两层的$\sigma$差了$k$倍,所以这个方向也是离散的。
所以我们需要对极值点的位置进行进一步的优化(即寻找亚像素级别的极值点)。
1.2.3.调整极值点位置
在检测到的极值点$X_0=(x_0,y_0,\sigma_0)^T$处做三元二阶泰勒展开:
\[\begin{align} f \left( \begin{bmatrix} x \\ y \\ \sigma \\ \end{bmatrix} \right) &= f \left( \begin{bmatrix} x_0 \\ y_0 \\ \sigma_0 \\ \end{bmatrix} \right) + \begin{bmatrix} \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial \sigma} \end{bmatrix} \left( \begin{bmatrix} x \\ y \\ \sigma \\ \end{bmatrix} - \begin{bmatrix} x_0 \\ y_0 \\ \sigma_0 \\ \end{bmatrix} \right) \\&+ \frac{1}{2} \left( \begin{bmatrix} x \\ y \\ \sigma \\ \end{bmatrix} - \begin{bmatrix} x_0 \\ y_0 \\ \sigma_0 \\ \end{bmatrix} \right)^T \begin{bmatrix} \frac{\partial^2 f}{\partial x \partial x},\frac{\partial^2 f}{\partial x \partial y},\frac{\partial^2 f}{\partial x \partial \sigma} \\ \frac{\partial^2 f}{\partial x \partial y},\frac{\partial^2 f}{\partial y \partial y},\frac{\partial^2 f}{\partial y \partial \sigma} \\ \frac{\partial^2 f}{\partial x \partial \sigma},\frac{\partial^2 f}{\partial y \partial \sigma},\frac{\partial^2 f}{\partial \sigma \partial \sigma} \end{bmatrix} \left( \begin{bmatrix} x \\ y \\ \sigma \\ \end{bmatrix} - \begin{bmatrix} x_0 \\ y_0 \\ \sigma_0 \\ \end{bmatrix} \right) \end{align}\]写成矢量形式:
\[f(\mathbf{X}) = f(\mathbf{X}_0) + \frac{\partial f^T}{\partial \mathbf{X}} \hat{\mathbf{X}} + \frac{1}{2} \hat{\mathbf{X}}^T \frac{\partial^2 f}{\partial \mathbf{X}^2} \hat{\mathbf{X}}\]然后使用牛顿法求得调整后的极值点。满足以下任意一个条件则牛顿法迭代终止:
- 新求得的极值点和上一个极值点在三个方向上的差异都小于0.5。此时认为算法收敛,不再迭代。
- 如果达到最大迭代次数,依然没有满足条件1,则迭代终止并舍弃该点。
此外,如果满足条件1,但是得到的新极值点和最初始的极值点$X_0$距离过远,这也是不合理的,因为泰勒展开是对$X_0$附近的函数近似,所以这种点也会被舍弃。
图像中导数的计算见:链接。
1.2.4.舍去低对比度的点
若:
\[\lvert f(\mathbf{X}) \rvert < \frac{T}{n}\]则舍去点$\mathbf{X}$(因为这样的点也会被认为是噪声)。$T$的定义同第1.2.1部分,$n$的定义同第1.1部分。$\mathbf{X}$为经过第1.2.3部分筛选后得到的极值点。$f$的计算见第1.2.3部分。
1.2.5.边缘效应的去除
SIFT想要提取的特征点为角点而非边缘,而前面一系列操作只能保证取到灰度值变换剧烈的点,而边缘点同样符合这一特征,因此我们将通过以下方式去除边缘点。
👉计算黑塞矩阵:
\[H(x,y) = \begin{bmatrix} D_{xx}(x,y) & D_{xy}(x,y) \\ D_{yx}(x,y) & D_{yy}(x,y) \end{bmatrix} = \begin{bmatrix} \frac{\partial^2 f}{\partial x \partial x} & \frac{\partial^2 f}{\partial x \partial y} \\ \frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y \partial y} \end{bmatrix}\]👉若矩阵行列式$Det(H) < 0$,则舍去该特征点。
👉若矩阵行列式和迹不满足:$\frac{Tr(H)^2}{Det(H)} < \frac{(\gamma_0 + 1)^2}{\gamma_0}$,则舍去该特征点,$\gamma_0$为有实际意义的经验值,通常设定为10。
这样做的原理在于:边缘在图像中表现为一条线,在垂直于线的方向灰度值变化剧烈,而在沿着线的方向灰度值变化较小;而角点则在多个方向上灰度值变化都比较剧烈。黑塞矩阵实际上是函数的二阶偏导构成的矩阵,可以反应函数的曲率变化状况,其同时也是一个二次型矩阵(见本文第2部分),有如下性质:
- 假定二次型矩阵$H$的两个特征值为$\alpha,\beta$,则$Det(H)=D_{xx}D_{yy}-(D_{xy})^2=\alpha \beta$,$Tr(H)=D_{xx}+D_{yy}=\alpha+\beta$。
- 实二次型矩阵的特征值异号时,该矩阵为不定矩阵,当黑塞矩阵为不定矩阵时,该临界点为非极值点。
- 黑塞矩阵的特征值标定了函数在相应特征向量方向上变化的快慢。
由性质1和2,我们可以推导出当$Det(H)<0$时,特征点为非极值点,所以舍去该点。
针对性质1和3,我们设$\alpha>\beta$且$\alpha = \gamma \beta$,有$\frac{Tr(H)^2}{Det(H)}=\frac{(\alpha+\beta)^2}{\alpha \beta}=\frac{(\gamma+1)^2}{\gamma}$。经过$Det(H)<0$的筛选后,得到的特征点的两个特征值$\alpha,\beta$都是同号的,即$\gamma>1$。函数$\frac{(\gamma+1)^2}{\gamma}=\gamma+\frac{1}{\gamma}+2$是一个对勾函数(见本文第3部分),因其$a>0,b>0$,所以图像分布在第一、三象限,又当$\gamma>1$时,其是单增的。所以当$\gamma$越大(即$\frac{Tr(H)^2}{Det(H)}$越大),说明$\alpha$和$\beta$的差异越大,即函数在该点不同方向上的变化非常不均匀,类似于边缘,所以此时也会舍去该点。也就是说我们希望$\frac{Tr(H)^2}{Det(H)}$小一点,于是有了$\frac{Tr(H)^2}{Det(H)} < \frac{(\gamma_0 + 1)^2}{\gamma_0}$这一判定条件。
1.3.确定关键点主方向
假设经过第1.2部分之后,在高斯差分金字塔中确定了某一极值点的坐标为$(x’,y’,\sigma’)$,设其在高斯金字塔中的坐标为$(x’,y’,\sigma’’)$,其中$\sigma^{''}$为高斯金字塔中最接近$\sigma^{'}$的尺度,然后我们在高斯金字塔中尺度为$\sigma^{''}$的那一层中以$(x’,y’)$为中心,$1.5\sigma^{''}$为半径,统计范围内所有像素点的梯度方向(gradient orientation)以及梯度幅值(即模,gradient magnitude)。
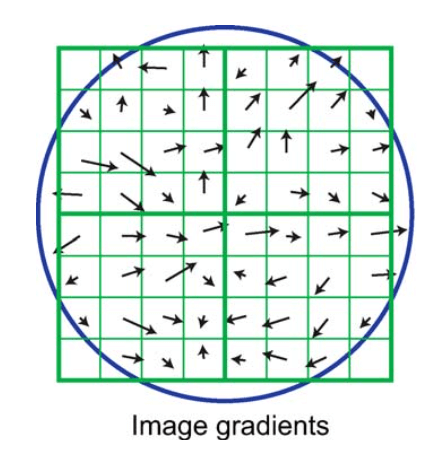
梯度幅值的计算:
\[m(x,y)=\sqrt{(L(x+1,y)-L(x-1,y))^2+(L(x,y+1)-L(x,y-1))^2}\]梯度方向的计算:
\[\theta(x,y) = tan^{-1}((L(x,y+1)-L(x,y-1))/(L(x+1,y)-L(x-1,y)))\]在继续下一步之前,通常还会对梯度幅值做一个高斯加权(尺度使用极值点的尺度):
\[m(x,y) = m(x,y) * G(x,y,1.5\sigma')\]然后每10度为一组,将360度分为36组,统计每组梯度方向内梯度幅值的和(简化示意图见下):
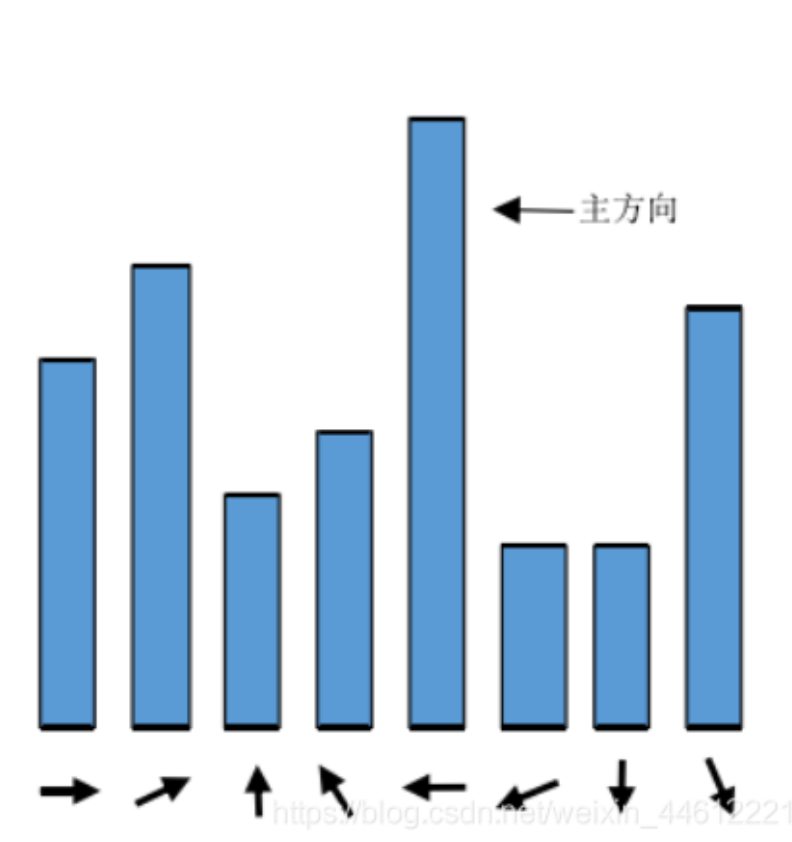
梯度幅值和最高的方向确定为该关键点的主方向,梯度幅值和大于最大梯度幅值和的80%以上的方向为该关键点的辅方向。对于既有主方向又有辅方向的关键点,我们通常将其看作是同一位置上的多个关键点,每个关键点分配一个方向(主方向或辅方向)。
1.4.构建关键点描述符
在之前的步骤中,我们确定了关键点的位置以及方向,那么我们该如何匹配两幅图像中的关键点呢?SIFT是通过描述符来完成关键点匹配的。描述符通常是一个128维的向量,构建步骤如下:
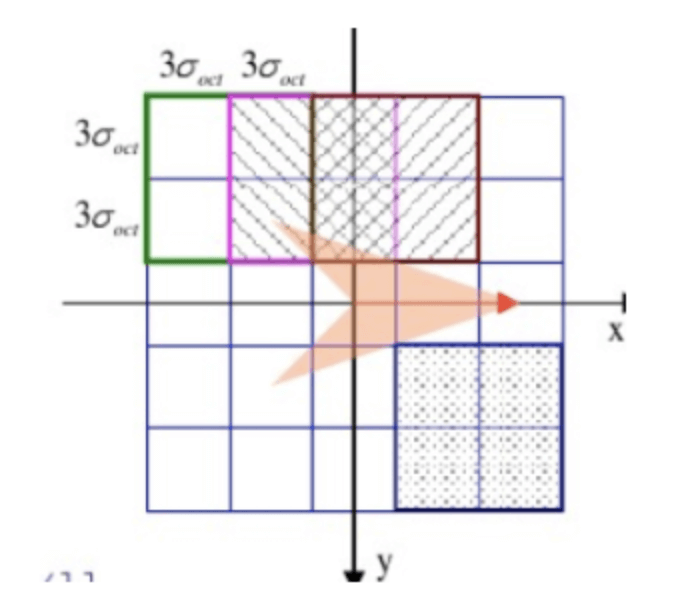
👉1.计算关键点周围区域的半径:
\[r=m \sigma \frac{d+1}{2} \sqrt{2}\]$r$就是下图以关键点为圆心的绿色圆圈的半径。$m$通常设为3,$d$通常设为4。$\sigma$为关键点的尺度。$m\sigma$为一个子块的边长(可以理解为子块的大小为$m\sigma \times m\sigma$个像素点)。

👉2.将计算区域旋转至主方向:如上图所示。这一步体现了SIFT的旋转不变性。假设主方向为$\theta$,旋转后像素点的新坐标为:
\[\begin{bmatrix} \hat{x} \\ \hat{y} \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{bmatrix} \times \begin{bmatrix} x \\ y \\ \end{bmatrix} \quad x,y \in [-r,r]\]由于旋转产生的像素值丢失,原论文是通过三线性插值来解决的。
👉3.在旋转后的实际计算区域内对每个像素点求其梯度幅值和方向,然后对每个梯度幅值乘以高斯权重参数,生成方向直方图。这一步和第1.3部分类似。
👉4.在旋转后的实际计算区域内,用$2\times 2$大小的窗口遍历滑动,每次窗口的中心都作为一个种子点,统计在窗口范围内所有像素点在8个梯度方向上的梯度幅值,按照8个方向的顺序,列出对应的8个梯度幅值,就相当于是一个种子点对应一个8维向量。那么$5 \times 5$个子块,一共可以产生$4\times 4=16$个种子点,也就是对应着$16\times 8 = 128$维向量,即该关键点的描述符。
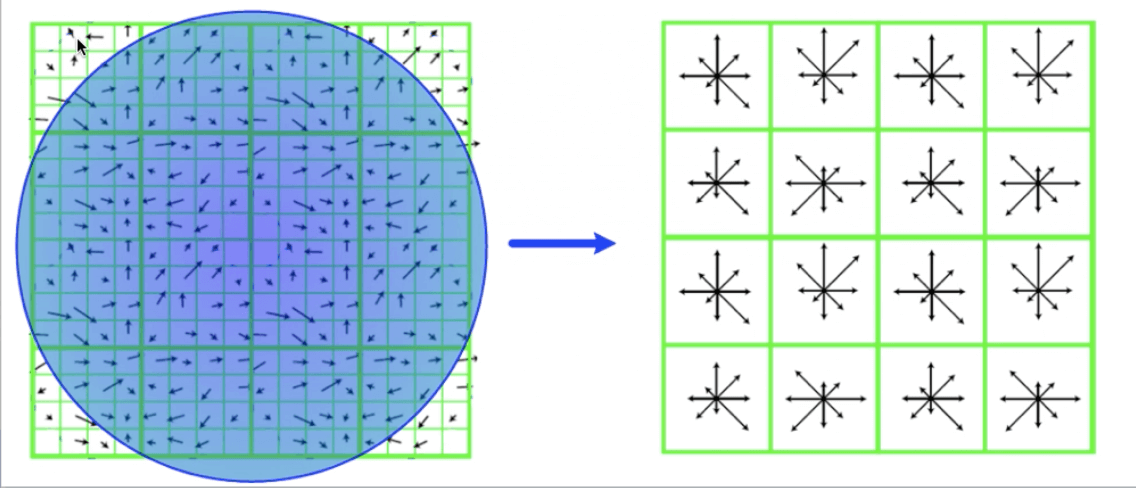
第1.4部分整个操作也都是基于高斯金字塔,而不是高斯差分金字塔。
2.二次型及其矩阵
含有$n$个变量$x_1,x_2,…,x_n$的二次齐次多项式:
\[\begin{align} f(x_1,x_2,...,x_n) &= a_{11}x_1^2 + 2a_{12}x_1x_2+2a_{13}x_1x_3+\cdots + 2a_{1n}x_1x_n \\&\quad + a_{22}x_2^2+2a_{23}x_2x_3+\cdots+2a_{2n}x_2x_n \\&\quad + a_{33}x_3^2+\cdots + 2a_{3n}x_3x_n \\&\quad + \cdots + a_{nn} x_n^2 \end{align}\]称为$n$元二次型,简称为二次型。
只含平方项的二次型,即形如:
\[f(x_1,x_2,...,x_n)=d_1x_1^2+d_2x_2^2+\cdots+d_nx_n^2\]称为二次型的标准形(或法式)。
👉二次型的矩阵表示法:
设$a_{ij}=a_{ji}$,
\[\begin{align} f(x_1,x_2,...,x_n) &= a_{11}x_1^2 + 2a_{12}x_1x_2+2a_{13}x_1x_3+\cdots + 2a_{1n}x_1x_n \\&\quad + a_{22}x_2^2+2a_{23}x_2x_3+\cdots+2a_{2n}x_2x_n \\&\quad + a_{33}x_3^2+\cdots + 2a_{3n}x_3x_n \\&\quad + \cdots + a_{nn} x_n^2 \\&= \begin{bmatrix} x_1 & x_2 & \cdots & x_n \\ \end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \\&= \mathbf{X}^T \mathbf{AX} \\ \end{align}\]二次型的矩阵是实对称矩阵。
3.对勾函数
形如:
\[f(x)=ax+\frac{b}{x}, (a\cdot b>0)\]的函数称为对勾函数。
定义域:$\{ x \mid x \neq 0 \}$。
值域:$(-\infty, -2\sqrt{ab}] \cup [2\sqrt{ab},+\infty)$。
当$a>0,b>0$时,图像在第一、三象限:

顶点坐标:$A=(\sqrt{\frac{b}{a}},2\sqrt{ab}),A’=(-\sqrt{\frac{b}{a}},-2\sqrt{ab})$。
当$a<0,b<0$时,图像在第二、四象限:
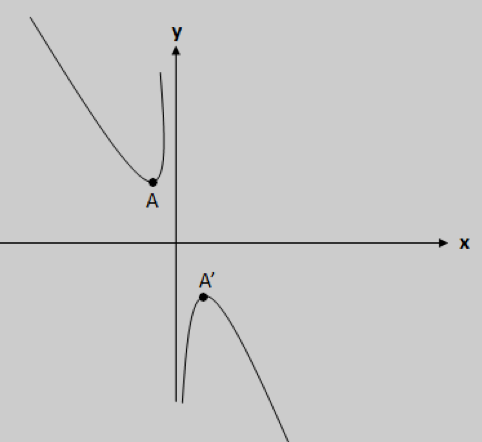
顶点坐标:$A=(-\sqrt{\frac{b}{a}},2\sqrt{ab}),A’=(\sqrt{\frac{b}{a}},-2\sqrt{ab})$。
4.cv::xfeatures2d::SIFT::create
1
2
3
4
5
6
7
static Ptr<SIFT> cv::xfeatures2d::SIFT::create (
int nfeatures = 0,
int nOctaveLayers = 3,
double contrastThreshold = 0.04,
double edgeThreshold = 10,
double sigma = 1.6
)
参数详解:
nfeatures:特征的数量,即关键点的个数。特征会按照其各自的得分从高到低排列,取前nfeatures个特征。特征的得分通过局部对比度计算得到。nOctaveLayers:每个octave内的层数,即第1.1部分提到的$n$。默认值为3,也是原论文中使用的值。而octave的数量则是通过图像分辨率自动算出来的。contrastThreshold:即第1.2.1部分和第1.2.4部分用到的$T$。edgeThreshold:即第1.2.5部分中的$\gamma_0$。sigma:即第1.1部分中的$\sigma_0$。
举个例子,SIFT检测到的关键点如下图所示:
