博客为参考《啊哈!算法》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.坑爹的奥数
枚举算法又叫做穷举算法。例如有一道奥数题:$?3 \times 6528 = 3? \times 8256$,让两个$?$等于同一个数字使得等式成立。代码实现如下:
1
2
3
4
int i;
for(i=1;i<=9;i++)
if((i*10+3)*6528 == (30+i)*8256)
printf("%d",i);
再看另外一道更复杂的题目:$???+???=???$,让9个$?$分别等于数字1~9使得等式成立,每个数字只使用一次。那么一共有多少种合理的组合呢?注意:$173+286=459$与$286+173=459$是同一种组合。枚举思路的代码实现见下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<iostream>
int main()
{
int a,b,c,d,e,f,g,h,i,total=0;
for(a=1;a<=9;a++)//第1个数的百位
{
for(b=1;b<=9;b++)//第1个数的十位
{
for(c=1;c<=9;c++)//第1个数的个位
{
for(d=1;d<=9;d++)//第2个数的百位
{
for(e=1;e<=9;e++)//第2个数的十位
{
for(f=1;f<=9;f++)//第2个数的个位
{
for(g=1;g<=9;g++)//第3个数的百位
{
for(h=1;h<=9;h++)//第3个数的十位
{
for(i=1;i<=9;i++)//第3个数的个位
{
if(a!=b && a!=c && a!=d && a!=e && a!=f && a!=g && a!=h && a!=i
&& b!=c && b!=d && b!=e && b!=f && b!=g && b!=h && b!=i
&& c!=d && c!=e && c!=f && c!=g && c!=h && c!=i
&& d!=e && d!=f && d!=g && d!=h && d!=i
&& e!=f && e!=g && e!=h && e!=i
&& f!=g && f!=h && f!=i
&& g!=h && g!=i
&& h!=i
&& a*100+b*10+c+d*100+e*10+f == g*100+h*10+i)
{
total++;
printf("%d%d%d+%d%d%d=%d%d%d\n",a,b,c,d,e,f,g,h,i);
}
}
}
}
}
}
}
}
}
}
printf("total=%d",total/2);//这里需要除以2
return 0;
}
if判断部分过于繁琐,对代码进行如下优化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<iostream>
int main()
{
int a[10],i,total=0,book[10],sum;
for(a[1]=1;a[1]<=9;a[1]++)//第1个数的百位
{
for(a[2]=1;a[2]<=9;a[2]++)//第1个数的十位
{
for(a[3]=1;a[3]<=9;a[3]++)//第1个数的个位
{
for(a[4]=1;a[4]<=9;a[4]++)//第2个数的百位
{
for(a[5]=1;a[5]<=9;a[5]++)//第2个数的十位
{
for(a[6]=1;a[6]<=9;a[6]++)//第2个数的个位
{
for(a[7]=1;a[7]<=9;a[7]++)//第3个数的百位
{
for(a[8]=1;a[8]<=9;a[8]++)//第3个数的十位
{
for(a[9]=1;a[9]<=9;a[9]++)//第3个数的个位
{
for(i=1;i<=9;i++)//初始化book数组
book[i]=0;
for(i=1;i<=9;i++)//如果某个数出现过就标记一下
book[a[i]]=1;
//统计共出现了多少个不同的数
sum=0;
for(i=1;i<=9;i++)
sum+=book[i];
//如果正好出现了9个不同的数,并且满足等式条件,则输出
if(sum==9 && a[1]*100+a[2]*10+a[3]+a[4]*100+a[5]*10+a[6]==
a[7]*100+a[8]*10+a[9])
{
total++;
printf("%d%d%d+%d%d%d=%d%d%d\n",a[1],a[2],a[3],a[4],a[5],a[6],
a[7],a[8],a[9]);
}
}
}
}
}
}
}
}
}
}
printf("total=%d",total/2);
return 0;
}
即使经过优化,但是整体代码还是很繁琐,我们将在第四章彻底解决这个问题。
2.炸弹人
如下图所示,假设只有一枚炸弹(上下左右四个方向爆炸),那么在哪里放置炸弹才可以消灭最多的敌人呢?

我们先将这个地图模型化。墙用#表示。炸弹是不能穿墙的。敌人用G表示,空地用.表示,当然炸弹只能放在空地上。
1
2
3
4
5
6
7
8
9
10
11
12
13
#############
#GG.GGG#GGG.#
###.#G#G#G#G#
#.......#..G#
#G#.###.#G#G#
#GG.GGG.#.GG#
#G#.#G#.#.###
##G...G.....#
#G#.#G###.#G#
#...G#GGG.GG#
#G#.#G#G#.#G#
#GG.GGG#G.GG#
#############
首先我们需要用一个二维字符数组来存储这个地图。枚举思路的代码实现见下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<stdio.h>
int main()
{
char a[20][21];//假设这里的地图大小不超过20*20
int i,j,sum,map=0,p,q,x,y,n,m;
//读入n和m,n表示有多少行字符,m表示每行有多少列
scanf("%d %d",&n,&m);
//读入n行字符
for(i=0;i<=n-1;i++)
scanf("%s",a[i]);
//用两重循环枚举地图中的每一点
for(i=0;i<=n-1;i++)
{
for(j=0;j<=m-1;j++)
{
//首先判断这个点是不是平地,是平地才可以被放置炸弹
if(a[i][j]=='.')
{
sum=0;//sum用来计数(可以消灭的敌人数),所以需要初始化为0
//将当前坐标i,j复制到两个新变量x,y中,以便向上下左右四个方向分别统计可以消灭的敌人数
//向上统计可以消灭的敌人数
x=i;y=j;
while(a[x][y]!='#')//判断是不是墙,如果不是墙就继续
{
//如果当前点是敌人,则进行计数
if(a[x][y]=='G')
sum++;
//x--的作用是继续向上统计
x--;
}
//向下统计可以消灭的敌人数
x=i;y=j;
while(a[x][y]!='#')
{
if(a[x][y]=='G')
sum++;
//x++的作用是继续向下统计
x++;
}
//向左统计可以消灭的敌人数
x=i;y=j;
while(a[x][y]!='#')
{
if(a[x][y]=='G')
sum++;
//y--的作用是继续向左统计
y--;
}
//向右统计可以消灭的敌人数
x=i;y=j;
while(a[x][y]!='#')
{
if(a[x][y]=='G')
sum++;
//y++的作用是继续向右统计
y++;
}
//更新map的值
if(sum>map)
{
//如果当前点所能消灭的敌人总数大于map,则更新map
map=sum;
//并用p和q记录当前点的坐标
p=i;
q=j;
}
}
}
}
printf("将炸弹放置在(%d,%d),最多可以消灭%d个敌人\n",p,q,map);
return 0;
}
输入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
13 13
#############
#GG.GGG#GGG.#
###.#G#G#G#G#
#.......#..G#
#G#.###.#G#G#
#GG.GGG.#.GG#
#G#.#G#.#.###
##G...G.....#
#G#.#G###.#G#
#...G#GGG.GG#
#G#.#G#G#.#G#
#GG.GGG#G.GG#
#############
可得到输出:
1
将炸弹放置在(9,9),最多可以消灭8个敌人
但如果我们将地图$(6,11)$的墙改为平地,小人默认站在$(3,3)$这个位置,如下图右:
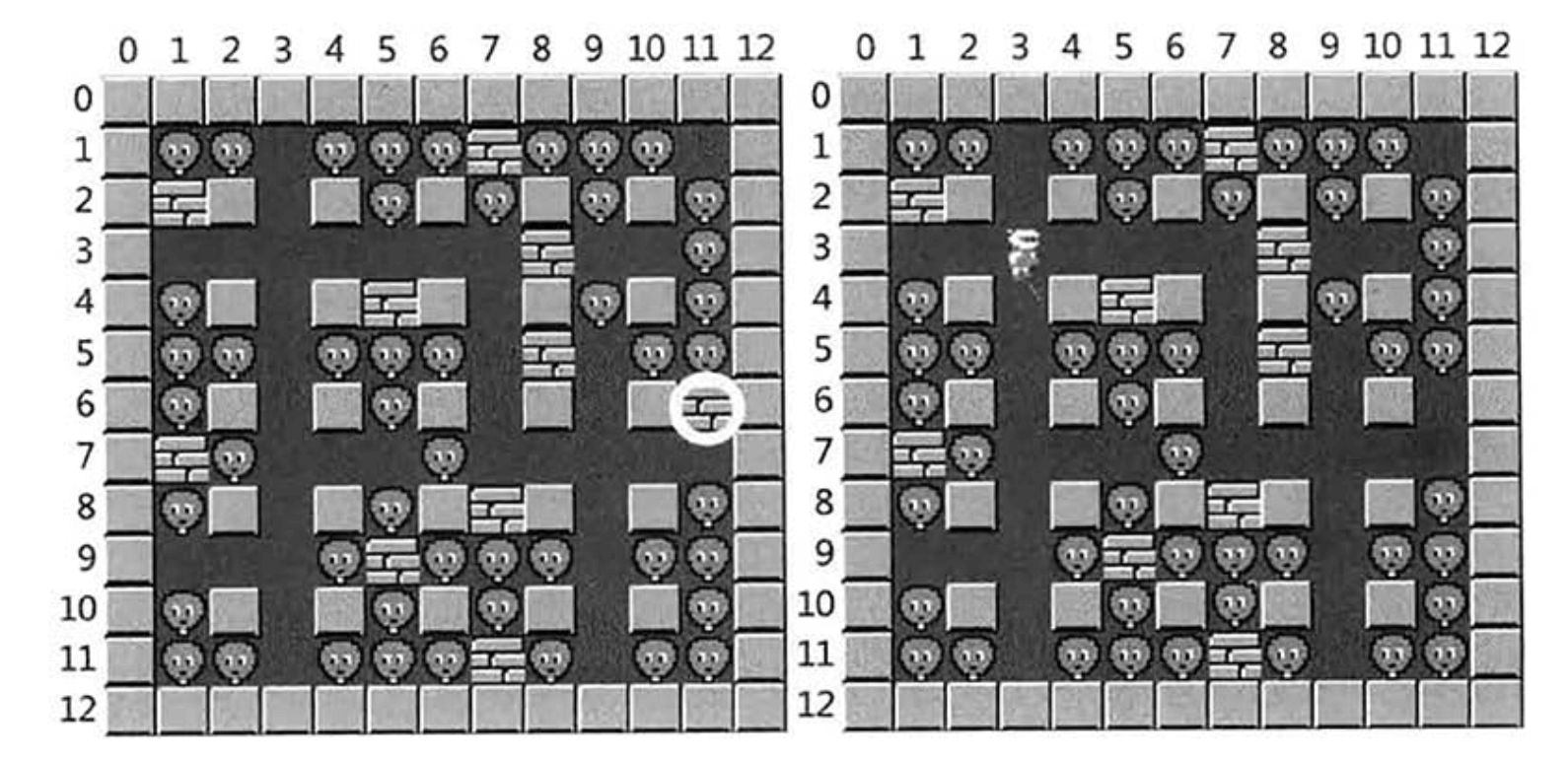
根据我们之前的算法,应该将炸弹放置在$(1,11)$处,最多可以消灭11个敌人。其实小人根本无法走到$(1,11)$处。所以正确的答案应该是将炸弹放在$(7,11)$处,最多可以消灭10个敌人。我们将在第四章讨论如何解决这种问题。
3.火柴棍等式
假设现在有$m(m\leqslant 24)$根火柴棍,希望拼出形如$A+B=C$的等式。等式中的$A$、$B$、$C$均是用火柴棍拼出来的整数(若该数非零,则最高位不能是0)。数字0~9的拼法如下图所示:

注意:
- 加号与等号各自需要两根火柴棍。
- 如果$A \neq B$,则$A+B=C$与$B+A=C$视为不同的等式($A$、$B$、$C$都大于0)。
- 所有根火柴棍必须全部用上。
那么究竟可以拼出多少个不同的形如$A+B=C$的等式呢?那最简单的办法就是分别枚举$A$、$B$、$C$了。接下来的问题就是:$A$、$B$、$C$的枚举范围是什么呢?因为最多有24根火柴棍,除去“+”和“=”占用的4根火柴棍,那么最多剩下20根火柴棍。而0~9这10个数字中,数字1需要用到的火柴棍最少,只需要2根火柴棍。而20根火柴棍最多能组成10个1,也就是$A$、$B$、$C$三个数的位数之和最多也只能是10位。此外,$C$是$A$、$B$、$C$中最大的:
- 如果$C$是10位数或9位数,那么$C$至少要用到20根或18根火柴棍,就没有多余的火柴棍分配给$A$和$B$了。
- 如果$C$是8位数,其至少占用16根火柴棍,假设$A$只占用2根使其至少可以是1,那么$B$最多可有2根火柴棍,所以$B$最大也只能是1,等式明显无法成立。
- 如果$C$是7位数,其至少占用14根火柴棍,假设$A$只占用2根使其至少可以是1,那么$B$最多可有4根火柴棍,所以$B$最大也只能是11,等式明显无法成立。
- 如果$C$是6位数,其至少占用12根火柴棍,假设$A$只占用2根使其至少可以是1,那么$B$最多可有6根火柴棍,所以$B$最大也只能是111,等式依然无法成立。
- 如果$C$是5位数,其至少占用10根火柴棍,假设$A$只占用2根使其至少可以是1,那么$B$最多可有8根火柴棍,所以$B$最大也只能是1111,等式依然无法成立。
- 如果$C$是4位数,其至少占用8根火柴棍,假设$A$只占用2根使其至少可以是1,那么$B$最多可有10根火柴棍。假设$C$是占用了8根火柴棍的4位数,那么$C$只能是1111,$A$是1,此时$B$得到最多的10根火柴棍,但$B$此时应该是1111-1=1110,10根火柴棍并得不到这个答案。如果$B$只拿9根火柴棍,剩余的1根给$C$或$A$,此时等式依然无法成立,所以$B$最多拿8根火柴棍,也就是$A$和$B$最大也不会超过1111。
枚举思路的代码实现见下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<stdio.h>
int fun(int x)
{
int num=0;//用来计数的变量,一定要记得初始化
int f[10]={6,2,5,5,4,5,6,3,7,6};//用一个数组来记录0~9每个数字需要用多少根火柴棍
while(x/10!=0)//如果x/10的商不等于0的话,说明这个数至少有两位
{
//获得x的末尾数字并将此数所需要用到的火柴棍根数累加到num中
num+=f[x%10];
x=x/10;//去掉x的末尾数字,例如x的值为123则现在x的值为12
}
//最后加上此时x所需用到的火柴棍的根数(此时x一定是一位数)
num+=f[x];
return num;//返回需要火柴棍的总根数
}
int main()
{
int a,b,c,m,i,sum=0;//sum是用来计数的,因此一定要初始化为0
scanf("%d",&m);//读入火柴棍的个数
//开始枚举a和b
for(a=0;a<=1111;a++)
{
for(b=0;b<=1111;b++)
{
c=a+b;
if(fun(a)+fun(b)+fun(c)==m-4)
{
printf("%d+%d=%d\n",a,b,c);
sum++;
}
}
}
printf("一共可以拼出%d个不同的等式",sum);
return 0;
}
可以输入18进行验证:
1
2
3
4
5
6
7
8
9
10
0+4=4
0+11=11
1+10=11
2+2=4
2+7=9
4+0=4
7+2=9
10+1=11
11+0=11
一共可以拼出9个不同的等式
4.数的全排列
123的全排列是123、132、213、231、312、321。如果我们想得到1234的全排列呢?枚举思路的代码实现见下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<stdio.h>
int main()
{
int a,b,c,d;
for(a=1;a<=4;a++)
{
for(b=1;b<=4;b++)
{
for(c=1;c<=4;c++)
{
for(d=1;d<=4;d++)
{
if(a!=b && a!=c && a!=d && b!=c && b!=d && c!=d)
printf("%d%d%d%d\n",a,b,c,d);
}
}
}
}
return 0;
}
那如果是输入一个指定点的数$n$,输出1~n的全排列,又该如何呢?按照枚举的思路可以实现,但非常繁琐,我们将在第四章解决这个问题。