博客为参考《程序是怎样跑起来的》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.用二进制数表示计算机信息的原因
👉第2章热身问答:
- 32位是几个字节?
- 因为8位=1字节,所以32位就是$32 \div 8 =4$字节。
- 二进制数01011100转换成十进制数是多少?
- 92。
- 二进制数00001111左移两位后,会变成原数的几倍?
- 4倍。
- 补码形式表示的8位二进制数11111111,用十进制数表示的话是多少?
- -1。
- 补码形式表示的8位二进制数10101010,用16位的二进制数表示的话是多少?
- 1111111110101010。使用原数的最高位1来填充高位。
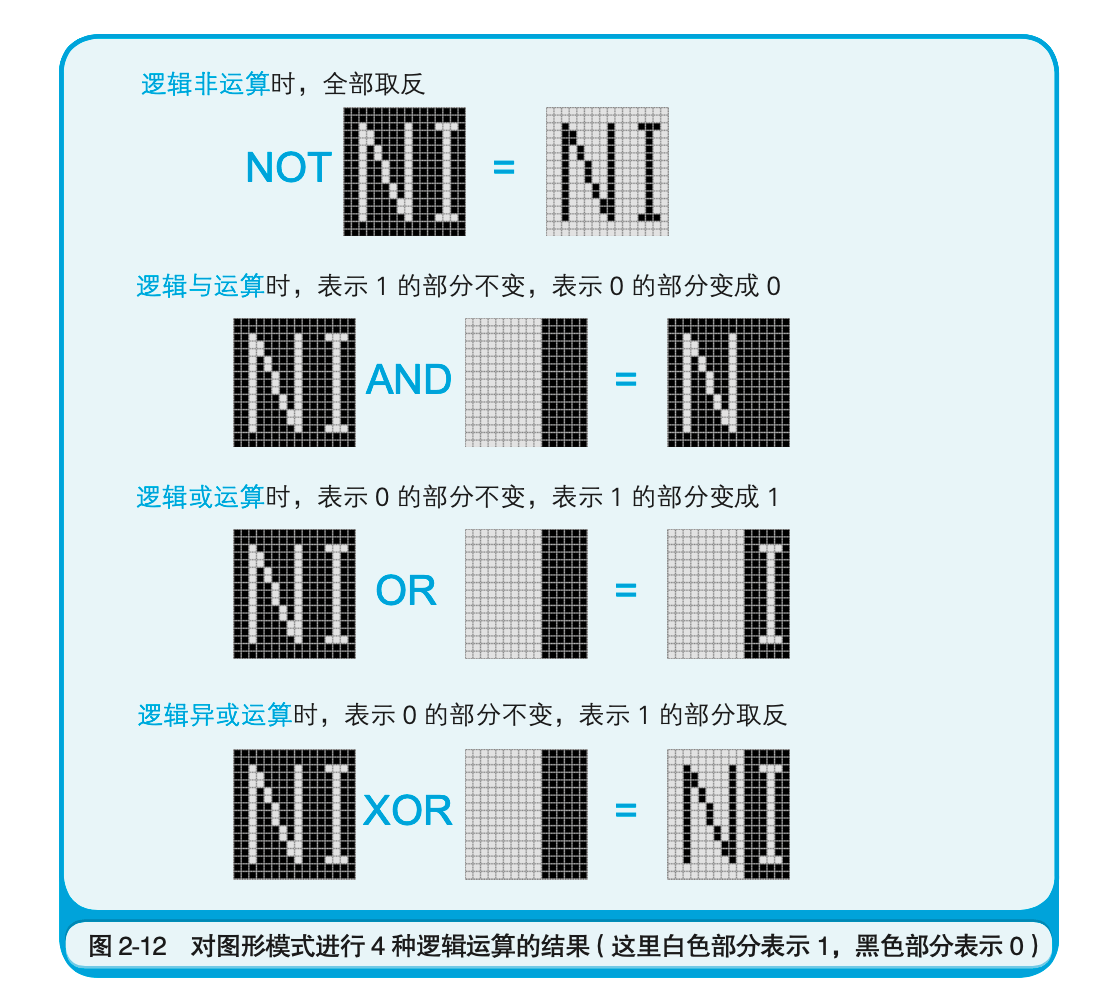
- 反转部分图形模式时,使用的是什么逻辑运算?
- XOR运算。因为XOR运算只反转与1相对应的位。NOT运算是反转所有的位。
在C和Java等高级语言编写的程序中,数值、字符串和图像等信息在计算机内部都是以二进制数值的形式来表现的。
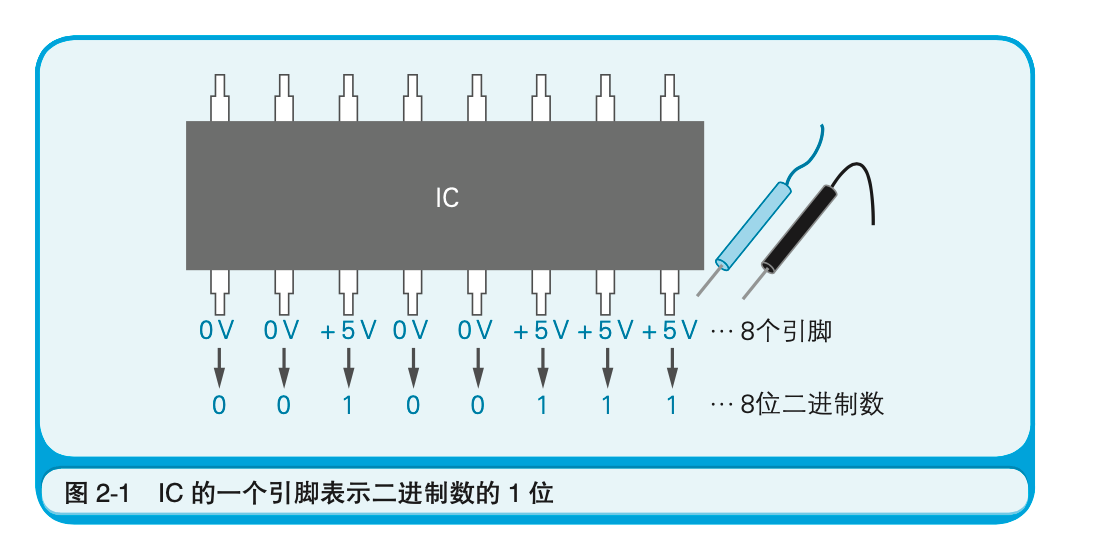
计算机内部都是由IC$^1$这种电子部件构成的。CPU(微处理器)和内存也是IC的一种。IC有几种不同的形状,有的像一条黑色蜈蚣,在其两侧有数个乃至数百个引脚;有的则像插花用的针盘,引脚在IC内部并排排列着。IC的所有引脚,只有直流电压0V或5V$^2$两个状态。也就是说,IC的一个引脚,只能表示两个状态。
- IC是集成电路(Integrated Circuit)的简称,有模拟IC和数字IC两种。本章介绍的是数字IC。
- 大部分IC的电源电压都是+5V。不过,为了控制电量的消耗,有的IC也会使用+5V以下的电压。如果IC使用的电源电压为+5V,那么引脚状态就不只是0V和+5V,还存在不接收电流信号的高阻抗(high impedance)的状态。但我们暂时不考虑高阻抗状态。
IC的这个特性,决定了计算机的信息数据只能用二进制数来处理。由于1位(一个引脚)只能表示两个状态,所以二进制的计数方式就变成了0、1、10、11、100$\cdots$这种形式。虽然二进制数并不是专门为IC而设计的,但是和IC的特性非常吻合(图2-1)。计算机处理信息的最小单位——位,就相当于二进制中的一位。位的英文bit是二进制数位(binary digit)的缩写。
二进制数的位数一般是8位、16位、32位$\cdots \cdots$也就是8的倍数,这是因为计算机所处理的信息的基本单位是8位二进制数。8位二进制数被称为一个字节$^1$。字节是最基本的信息计量单位。位是最小单位,字节是基本单位。内存和磁盘都使用字节单位来存储和读写数据,使用位单位则无法读写数据。因此,字节是信息的基本单位。
- 字节是由bite(咬)一词而衍生出来的词语。8位(8 bit)二进制数,就类似于“咬下的一口”,因此被视为信息的基本单位。
用字节单位处理数据时,如果数字小于存储数据的字节数(=二进制数的位数),那么高位上就用0填补。例如,100111这个6位二进制数,用8位(=1字节)表示时为00100111,用16位(=2字节)表示时为0000000000100111。奔腾等32位微处理器,具有32个引脚以用于信息的输入和输出。也就是说,奔腾一次可以处理32位(32位=4字节)的二进制数信息。
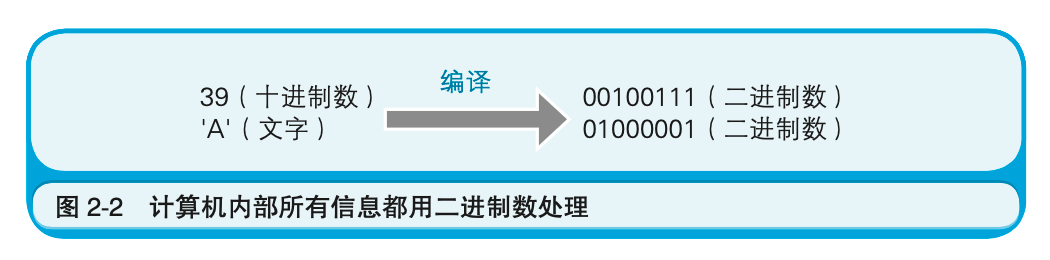
程序中,即使是用十进制数和文字等记述信息,在编译后也会转换成二进制数的值,所以,程序运行时计算机内部处理的也是用二进制数表示的信息(图2-2)。
对于用二进制数表示的信息,计算机不会区分它是数值、文字,还是某种图片的模式等,而是根据编写程序的各位对计算机发出的指示来进行信息的处理(运算)。
2.什么是二进制数

二进制的基数为2,图2-3中的$2^0,2^1,2^2,…$称为位权。数字的位数不同,位权也不同。同理,十进制的基数为10。
3.移位运算和乘除运算的关系
移位运算指的是将二进制数值的各数位进行左右移位(shift=移位)的运算。移位有左移(向高位方向)和右移(向低位方向)两种。在一次运算中,可以进行多个数位的移位操作。
代码清单2-1中列出的是把变量a中保存的十进制数值39左移两位后再将运算结果存储到变量b中的C语言程序。

无论程序中使用的是几进制,计算机内部都会将其转换成二进制数来处理,因此都能进行移位操作。移位后,空出来的低位要进行补0操作。不过,这一规则只适用于左移运算。至于右移时空出来的高位要进行怎样的操作,我们会在后面说明。此外,移位操作使最高位或最低位溢出的数字,直接丢弃就可以了。
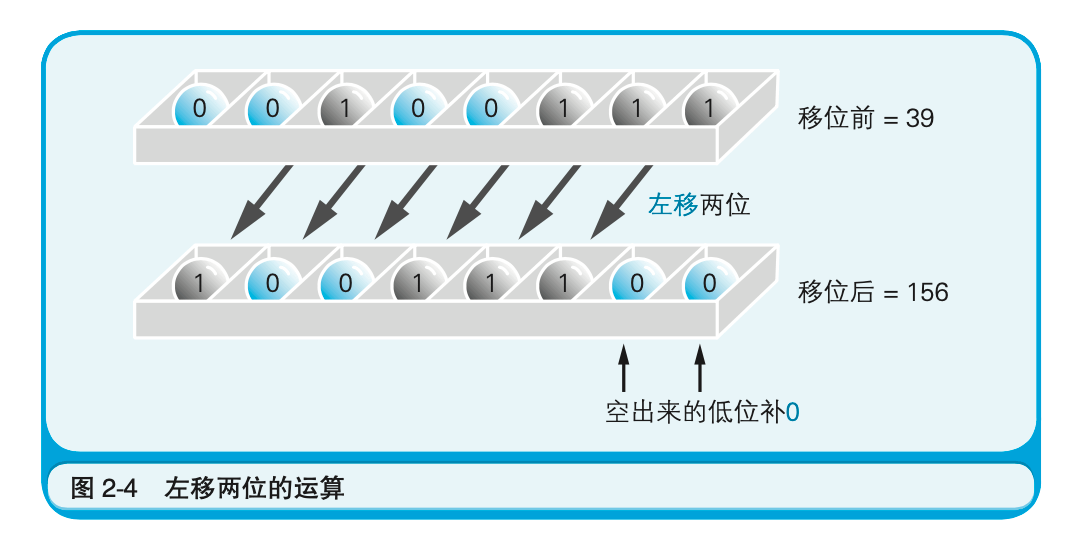
这里没有考虑数值的符号,后续会说明原因。
移位运算也可以通过数位移动来代替乘法运算和除法运算。二进制数左移后就会变成原来的2倍、4倍、8倍$\cdots \cdots$反之,二进制数右移后则会变成原来的$\frac{1}{2}$、$\frac{1}{4}$、$\frac{1}{8}$ $\cdots \cdots$。
4.便于计算机处理的“补数”
二进制数中表示负数值时,一般会把最高位作为符号来使用,因此我们把这个最高位称为符号位。符号位是0时表示正数,符号位是1时表示负数。那么-1用8位二进制数来表示的话是什么样的呢?其实10000001是错误答案,正确答案应该是11111111。
计算机在做减法运算时,实际上内部是在做加法运算。用加法运算来实现减法运算。为此,在表示负数时就需要使用“二进制的补数”。补数就是用正数来表示负数。
关于原码、反码、补码的讲解请见:链接。
例如对1-1的计算如下图所示:

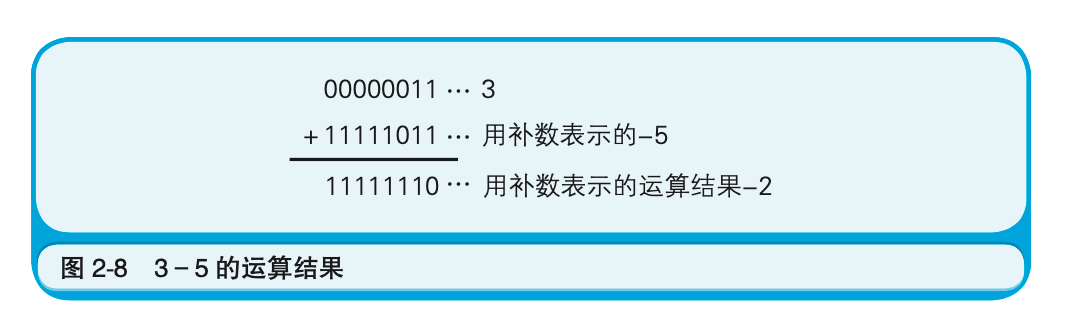
有一点需要注意,当运算结果为负数时,计算结果的值也是以补数的形式来表示的。例如3-5的计算如下图所示:
5.逻辑右移和算术右移的区别
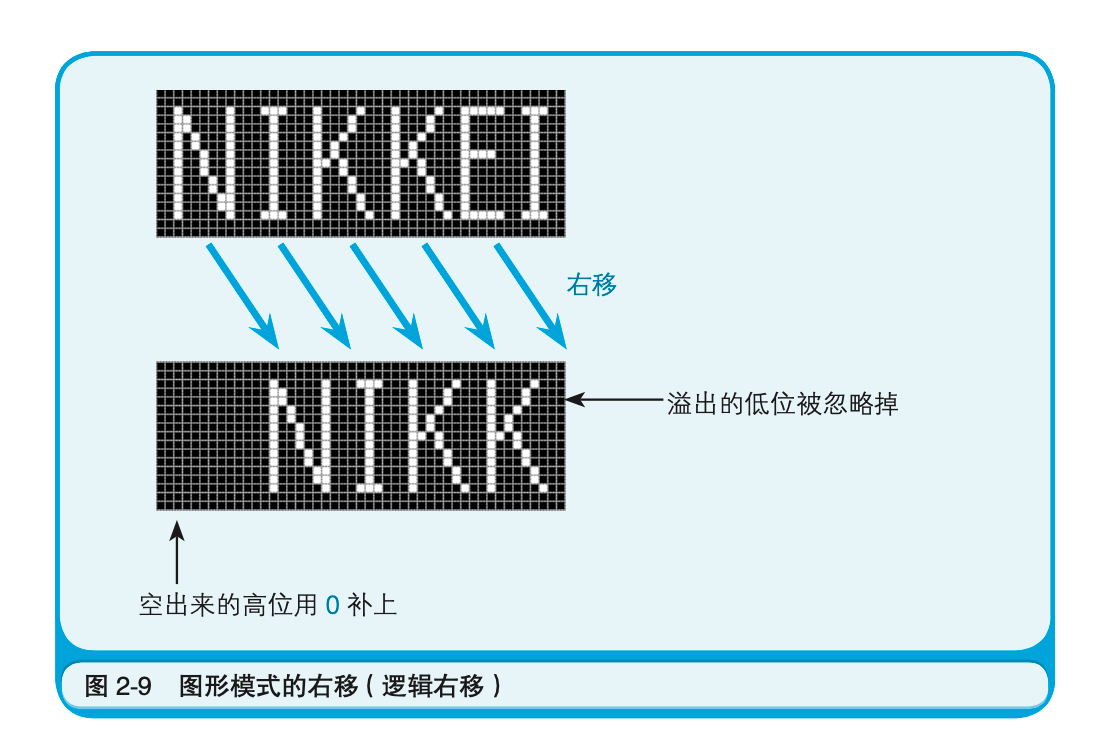
右移有移位后在最高位补0和补1两种情况。当二进制数的值表示图形模式而非数值时,移位后需要在最高位补0。类似于霓虹灯往右滚动的效果。这就称为逻辑右移(图2-9)。
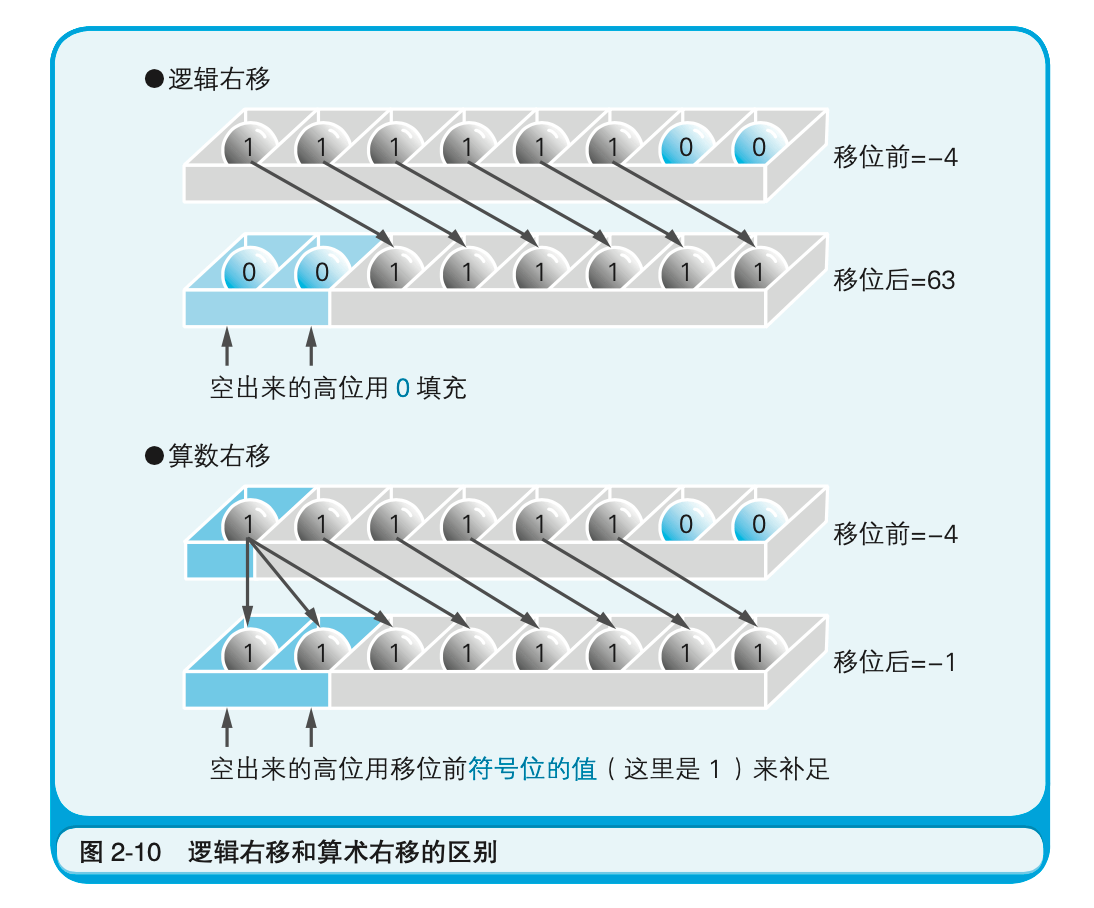
将二进制数作为带符号的数值进行运算时,移位后要在最高位填充移位前符号位的值(0或1)。这就称为算术右移。如果数值是用补数表示的负数值,那么右移后在空出来的最高位补1,就可以正确地实现$\frac{1}{2}$、$\frac{1}{4}$、$\frac{1}{8}$等的数值运算。如果是正数,只需在最高位补0即可。
现在我们来看一个右移的例子。将-4(=11111100)右移两位。这时,逻辑右移的情况下结果就会变成00111111,也就是十进制数63,显然不是-4的$\frac{1}{4}$。而算术右移的情况下,结果就会变成11111111,用补数表示就是-1,即-4的$\frac{1}{4}$(图2-10)。
只有在右移时才必须区分逻辑位移和算术位移。左移时,无论是图形模式(逻辑左移)还是相乘运算(算术左移),都只需在空出来的低位补0即可。
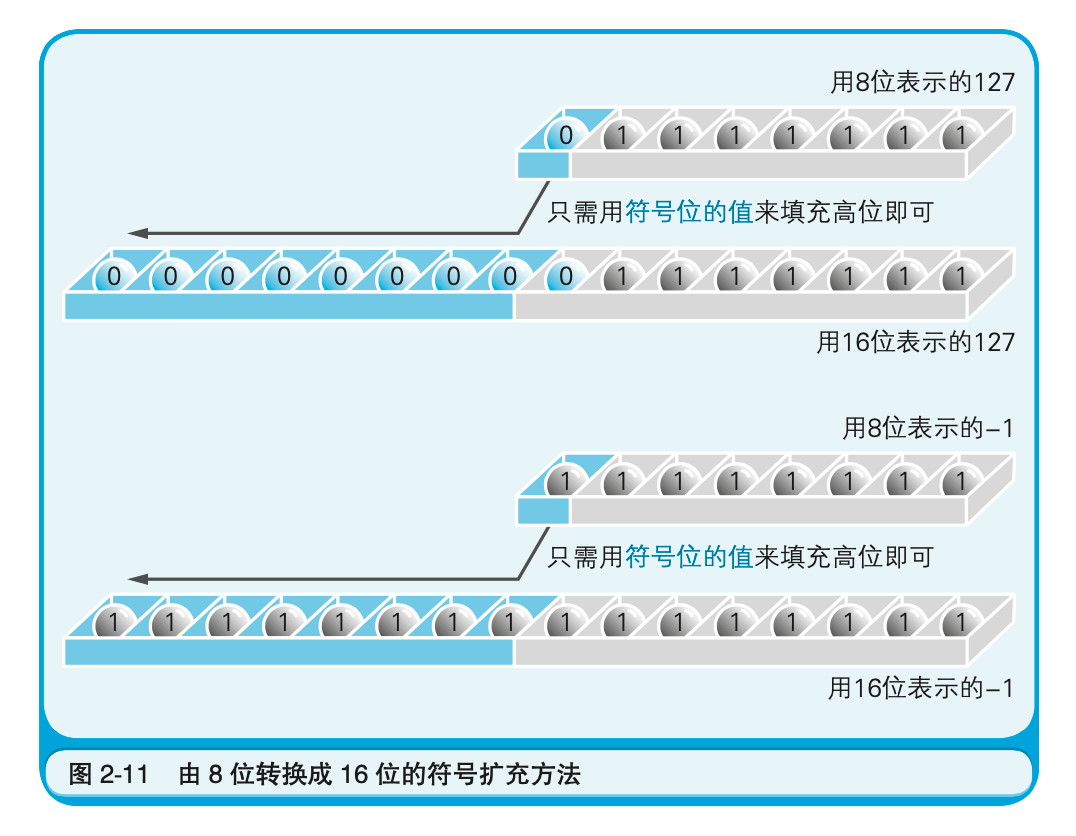
下面顺便介绍一下符号扩充。以8位二进制数为例,符号扩充就是指在保持值不变的前提下将其转换成16位和32位的二进制数。将01111111这个正的8位二进制数转换成16位二进制数时,很容易就能得出0000000001111111这个正确结果,但是像11111111这样用补数来表示的数值,该如何处理比较好呢?实际上处理方法非常简单,将其表示成1111111111111111就可以了。也就是说,不管是正数还是用补数表示的负数,都只需用符号位的值(0或者1)填充高位即可。这就是符号扩充的方法。图2-11向我们展示了将符号位扩充到高位的具体流程。
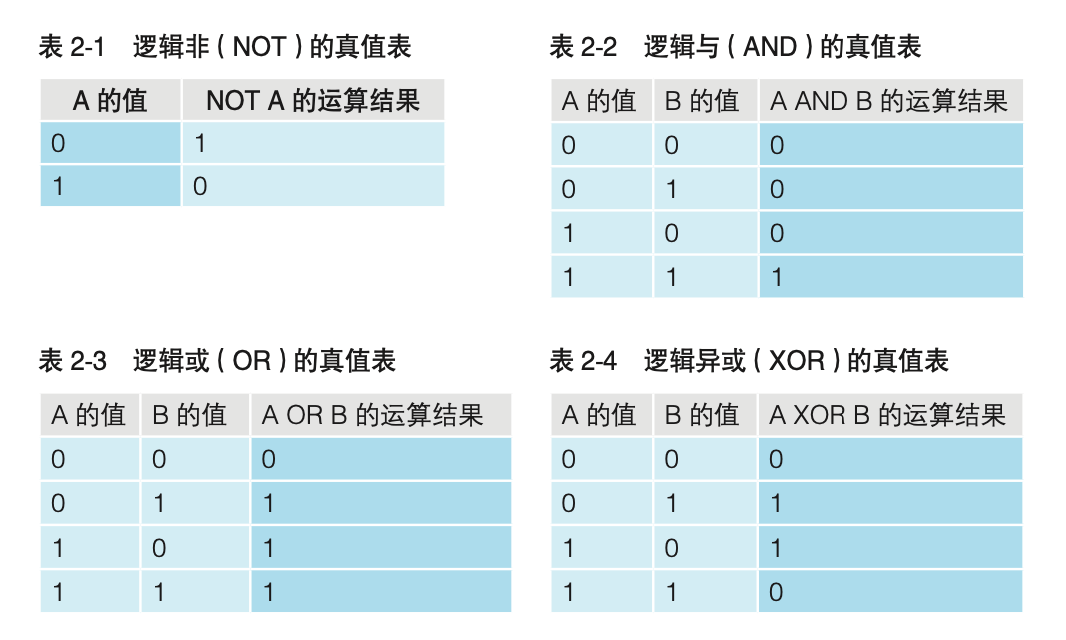
6.掌握逻辑运算的窍门
在运算中,与逻辑相对的术语是算术。将二进制数表示的信息作为四则运算的数值来处理就是算术。而像图形模型那样,将数值处理为单纯的0和1的罗列就是逻辑。
计算机能处理的运算,大体可分为算术运算和逻辑运算。算术运算是指加减乘除四则运算。逻辑运算是指对二进制数各数字位的0和1分别进行处理的运算,包括逻辑非(NOT运算)、逻辑与(AND运算)、逻辑或(OR运算)和逻辑异或(XOR运算$^1$)四种。
- XOR是英语exclusive or的缩写。有时也将XOR称为EOR。
表2-1~表2-4总结了各逻辑运算的结果。这些表称为真值表。