博客为参考《程序是怎样跑起来的》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.将0.1累加100次也得不到10
👉第3章热身问答:
- 二进制数0.1,用十进制数表示的话是多少?
- 0.5。
- 用小数点后有3位的二进制数,能表示十进制数0.625吗?
- 能表示。十进制数0.625转换成二进制数是0.101。
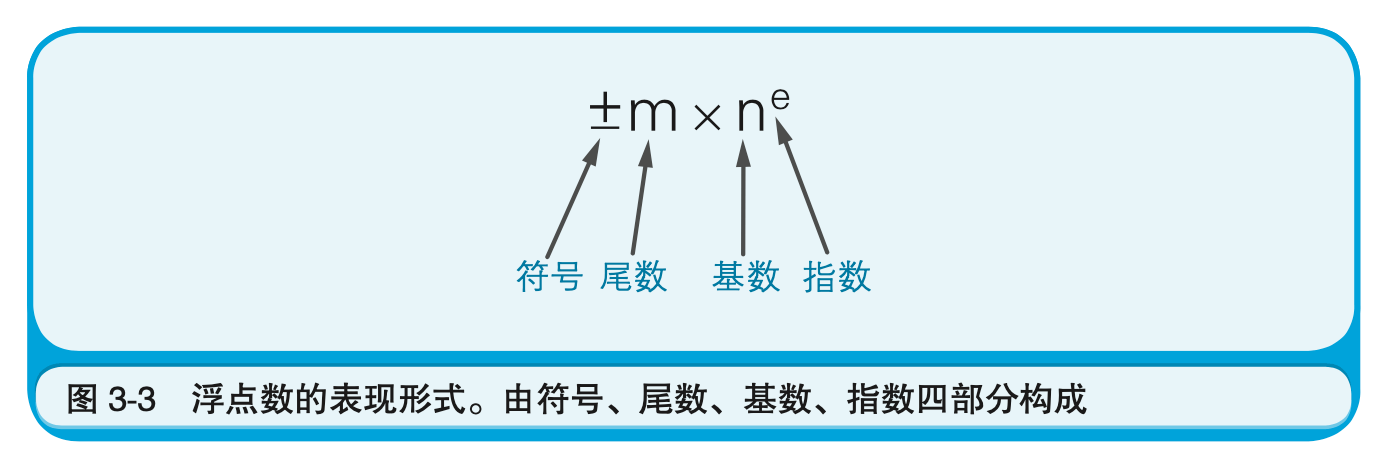
- 将小数分为符号、尾数、基数、指数4部分进行表现的形式称为什么?
- 浮点数(浮点数形式)。浮点数是指把小数用“符号 尾数 $\times$ 基数的指数次幂”这种形式来表示。
- 二进制数的基数是多少?
- 2。
- 通过把0作为数值范围的中间值,从而在不使用符号位的情况下来表示负数的表示方法称为什么?
- EXCESS系统表现。EXCESS是“剩余的”的意思。例如,把01111111看作是0的话,比这个数小1的01111110就是-1。
- 10101100.01010011这个二进制数,用十六进制数表示的话是多少?
- AC.53。整数部分和小数部分一样,二进制数的4位,就相当于十六进制数的1位。
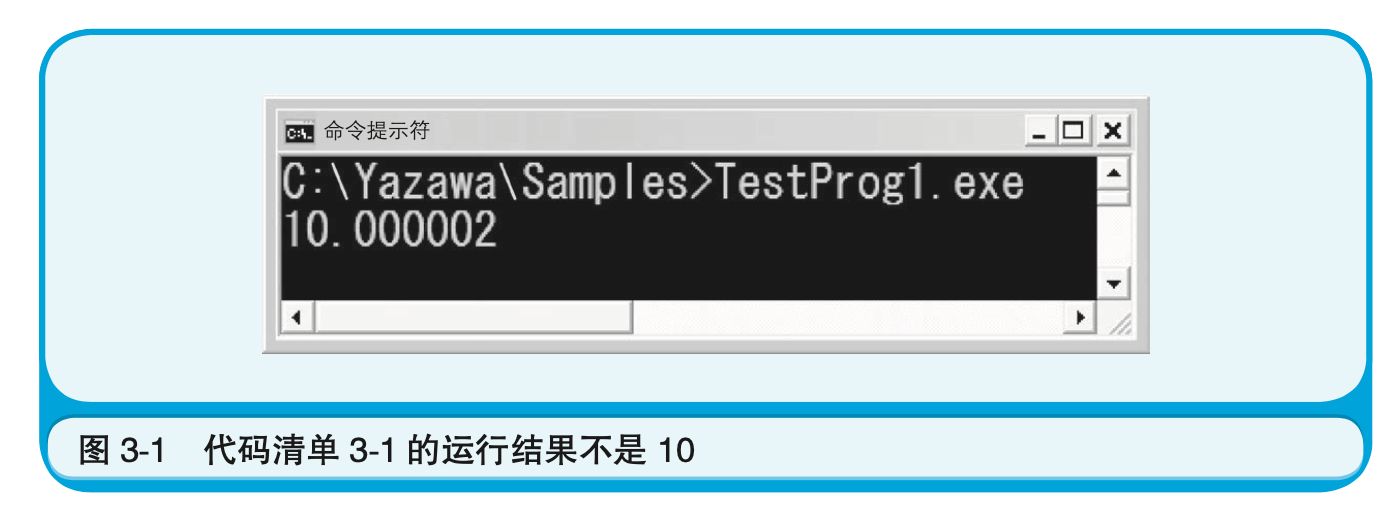
首先,我们来看一个计算机运算错误(无法得到正确结果)的例子。代码清单3-1是将0.1累加100次,然后将结果输出到显示器上的C语言程序。

上述代码运行后,显示器上显示的结果并不是10(图3-1)。
2.用二进制数表示小数
由于计算机内部所有的信息都是以二进制数的形式来处理的,因此在这一点上,整数和小数并无差别。不过,使用二进制数来表示整数和小数的方法却有很大的不同。
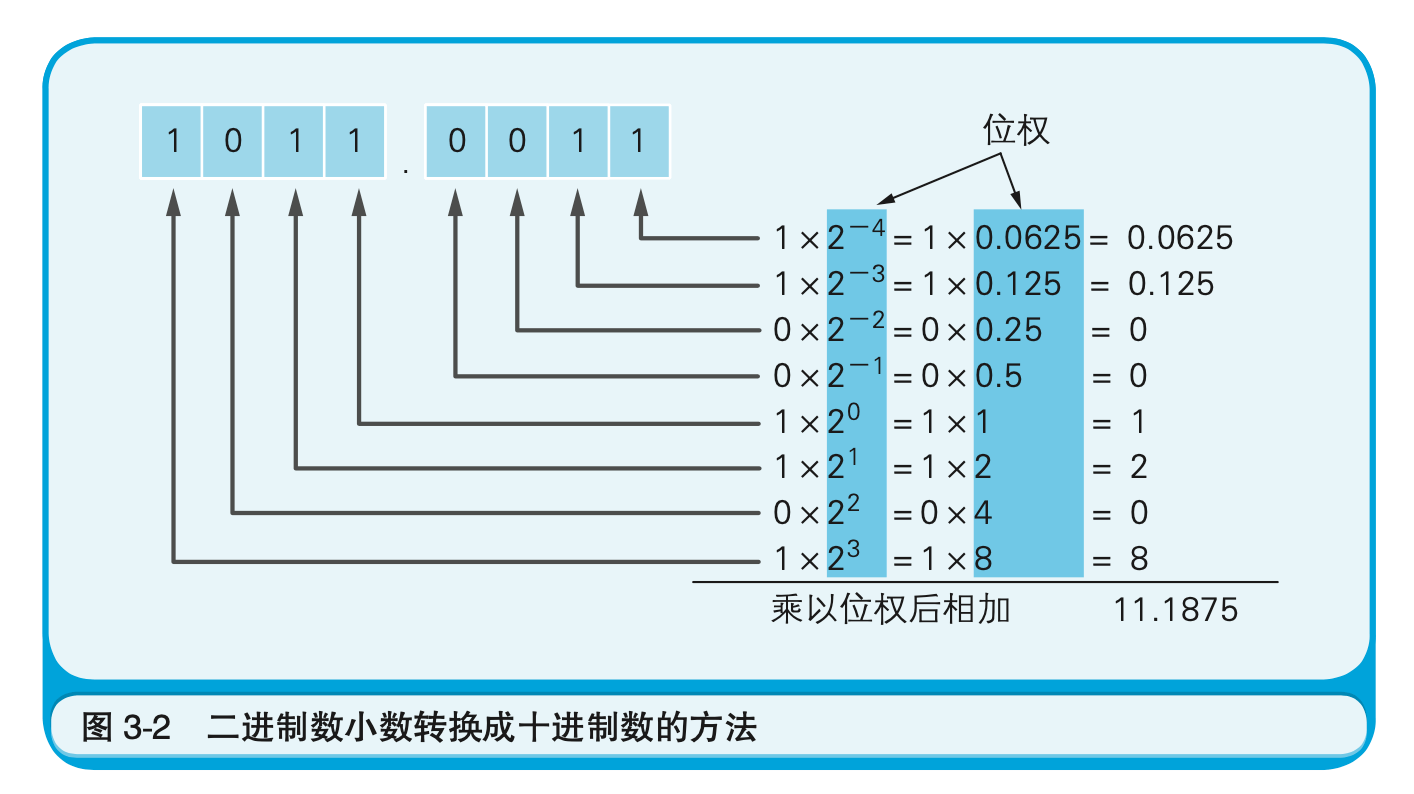
举个例子,把1011.0011这个有小数点的二进制数转换成十进制数。
3.计算机运算出错的原因
计算机之所以会出现运算错误,是因为“有一些十进制数的小数无法转换成二进制数”。例如,十进制数0.1,就无法用二进制数正确表示,小数点后面即使有几百位也无法表示。
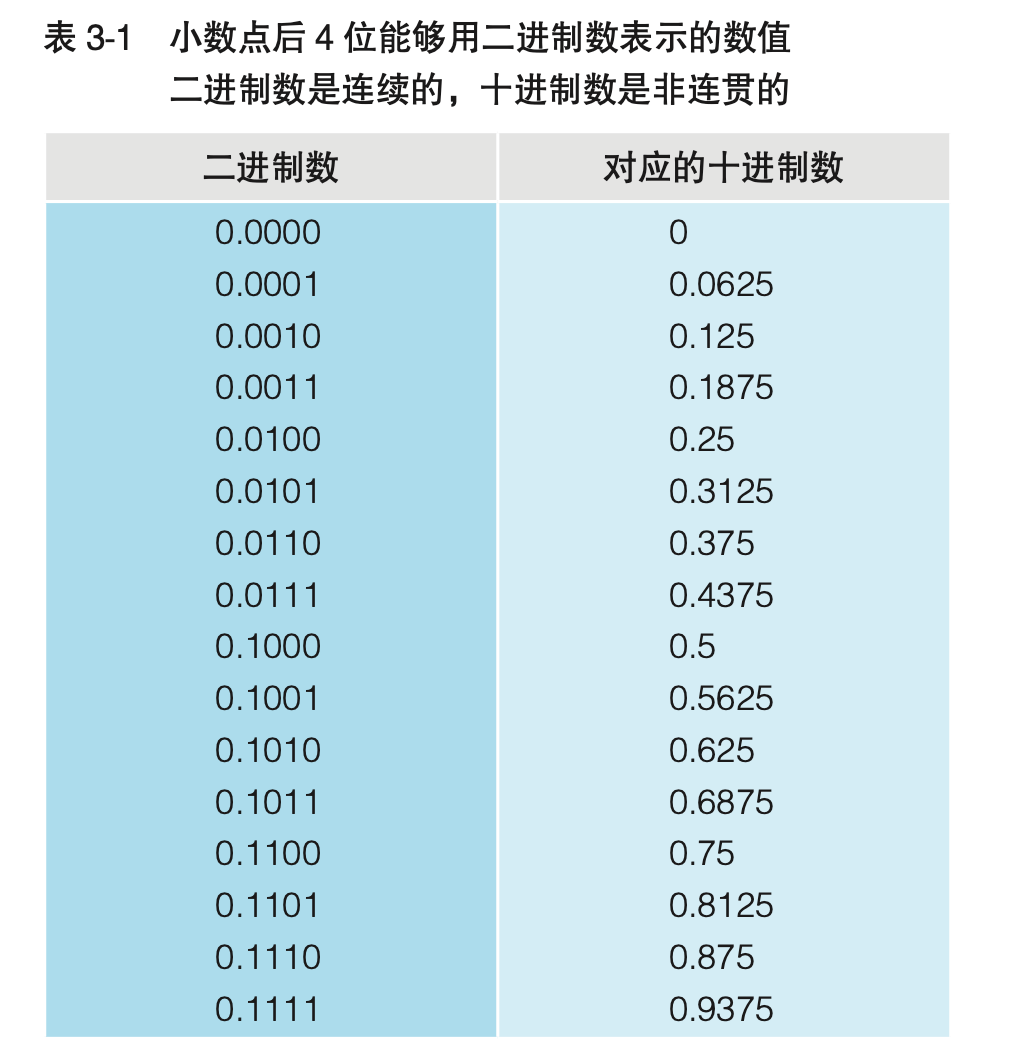
图3-2中,小数点后4位用二进制数表示时的数值范围为0.0000~0.1111。因此,这里只能表示0.5、0.25、0.125、0.0625这四个二进制数小数点后面的位权组合而成(相加总和)的小数。将这些数值组合后能够表示的数值,即为表3-1中所示的无序的十进制数。
实际上,十进制数0.1转换成二进制后,会变成0.00011001100$\cdots$(1100循环)这样的循环小数。这和无法用十进制数来表示$\frac{1}{3}$是一样的道理。$\frac{1}{3}$就是0.3333$\cdots$,同样是循环小数。
计算机是无法处理无限循环的小数的。因此,在遇到循环小数时,计算机就会根据变量数据类型所对应的长度将数值从中间截断或者四舍五入。
4.什么是浮点数
像1011.0011这样带小数点的表现形式,完全是纸面上的二进制数表现形式,在计算机内部是无法使用的。那么,实际上计算机是以什么样的表现形式来处理小数的呢?
很多编程语言中都提供了两种表示小数的数据类型,分别是双精度浮点数和单精度浮点数。双精度浮点数类型用64位、单精度浮点数类型用32位来表示全体小数$^1$。
浮点数$^2$是指用符号、尾数、基数和指数这四部分来表示的小数(图3-3)。因为计算机内部使用的是二进制数,所以基数自然就是2。因此,实际的数据中往往不考虑基数,只用符号、尾数、指数这三部分即可表示浮点数。也就是说,64位(双精度浮点数)和32位(单精度浮点数)的数据,会被分为三部分来使用(图3-4)。
- 双精度浮点数能够表示的正数范围是$4.94065645841247 \times 10^{-324}$~$1.79769313486232 \times 10^{308}$,负数范围是$-1.79769313486232 \times 10^{308}$~$-4.94065645841247 \times 10^{-324}$。单精度浮点数能够表示的正数范围是$1.401298 \times 10^{-45}$~$3.402823 \times 10^{38}$,负数范围是$-3.402823 \times 10^{38}$~$-1.401298 \times 10^{-45}$。不过,正如正文中所介绍的那样,在这些范围中,有些数值是无法正确表示的。
- 像$0.12345 \times 10^3$和$0.12345 \times 10^{-1}$这样使用与实际小数点位置不同的书写方法来表示小数的形式称为浮点数。与浮点数相对的是定点数,使用定点数表示小数时,小数点的实际位置固定不变。例如,$0.12345 \times 10^3$和$0.12345 \times 10^{-1}$用定点数来表示的话即为$123.45$和$0.012345$。
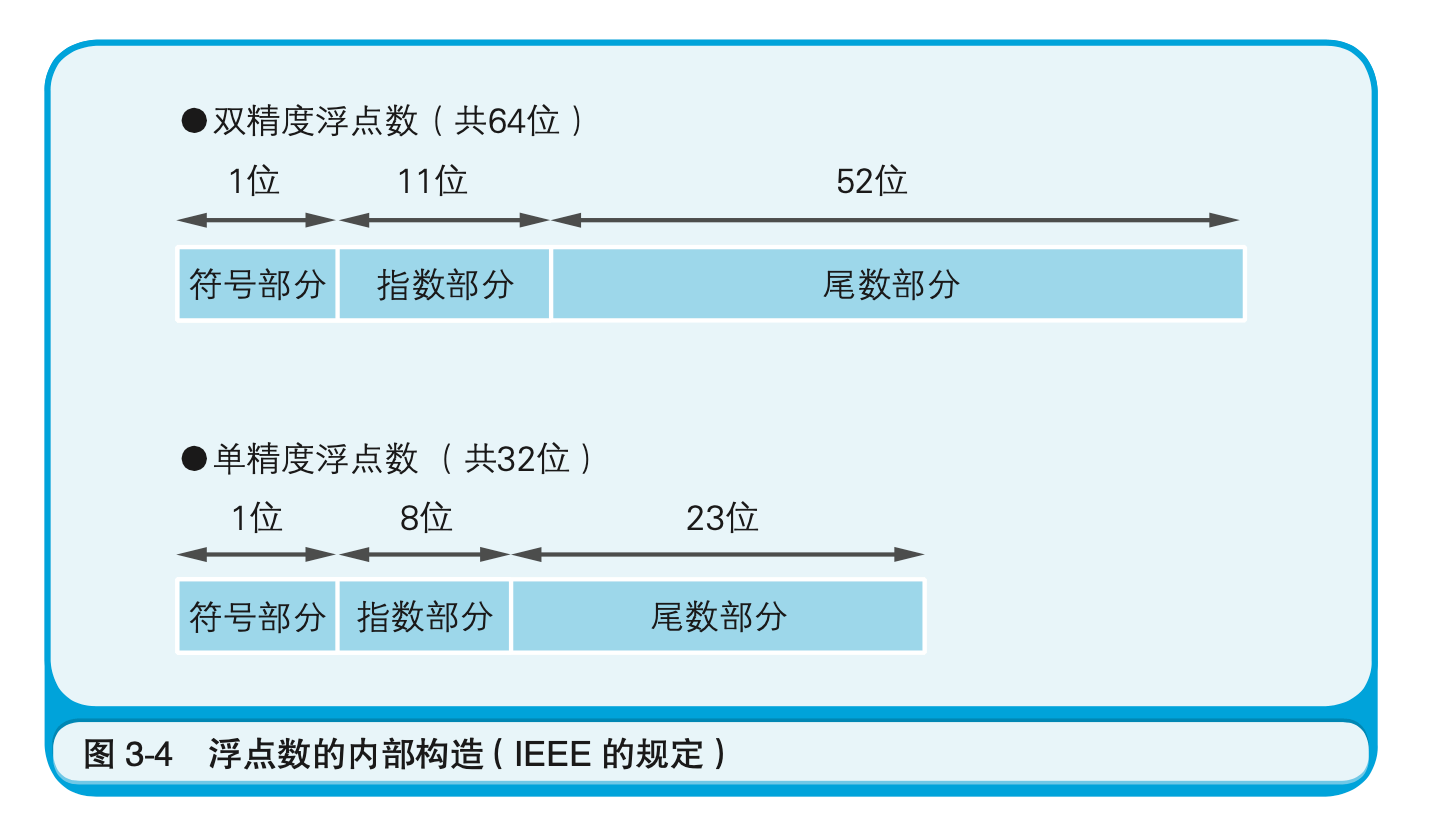
浮点数的表现方式有很多种,这里我们使用最为普遍的IEEE$^1$标准。双精度浮点数和单精度浮点数在表示同一个数值时使用的位数不同。此外,双精度浮点数能够表示的数值范围要大于单精度浮点数。
- IEEE(Institute of Electrical and Electronics Engineers)是指美国电气和电子工程师协会。该协会制定了计算机领域的各种规定。
符号部分是指使用一个数据位来表示数值的符号。该数据位是1时表示负,为0时则表示“正或者0”。
尾数部分和指数部分并不只是单单存储着用整数表示的二进制数。尾数部分用的是“将小数点前面的值固定为1的正则表达式”,而指数部分用的则是“EXCESS系统表现”。
5.正则表达式和EXCESS系统
尾数部分使用正则表达式$^1$,可以将表现形式多样的浮点数统一为一种表现形式。例如,十进制数0.75就有很多种表现形式,如图3-5所示。虽然它们表示的都是同一个数值,但因为表现方法太多,计算机在处理时会比较麻烦。因此,为了方便计算机处理,需要制定一个统一的规则。例如,十进制数的浮点数应该遵循“小数点前面是0,小数点后面第1位不能是0”这样的规则。根据这个规则,0.75就是“$0.75 \times 10$的0次幂”,也就是说,只能用尾数部分是0.75、指数部分是0这个方法来表示。根据这个规则来表示小数的方式,就是正则表达式。

- 按照特定的规则来表示数据的形式即为正则表达式。除小数之外,字符串以及数据库等,也都有各自的正则表达式。
二进制数也是同样的道理。在二进制数中,我们使用的是“将小数点前面的值固定为1的正则表达式”。而且,第1位的1在实际的数据中不保存。由于第1位必须是1,因此,省略该部分后就节省了一个数据位,从而也就可以表示更多的数据范围(虽然不算太多)。
单精度浮点数的正则表达式的具体例子如图3-6所示。单精度浮点数中,尾数部分是23位,但由于第1位的1被省略了,所以实际上可以表示24位的数值。双精度浮点数的表示方法也是如此,只是位数不同而已。

接下来,让我们一起来看一下指数部分中使用的EXCESS系统,使用这种方法主要是为了表示负数时不使用符号位。在某些情况下,在指数部分,需要通过“负多少次幂”的形式来表示负数。EXCESS系统表现是指,通过将指数部分表示范围的中间值设为0,使得负数不需要用符号来表示。也就是说,当指数部分是8位单精度浮点数时,最大值11111111=255的1/2,即01111111=127(小数部分舍弃)表示的是0,指数部分是11位双精度浮点数时,11111111111=2047的1/2,即01111111111=1023(小数部分舍弃)表示的是0。
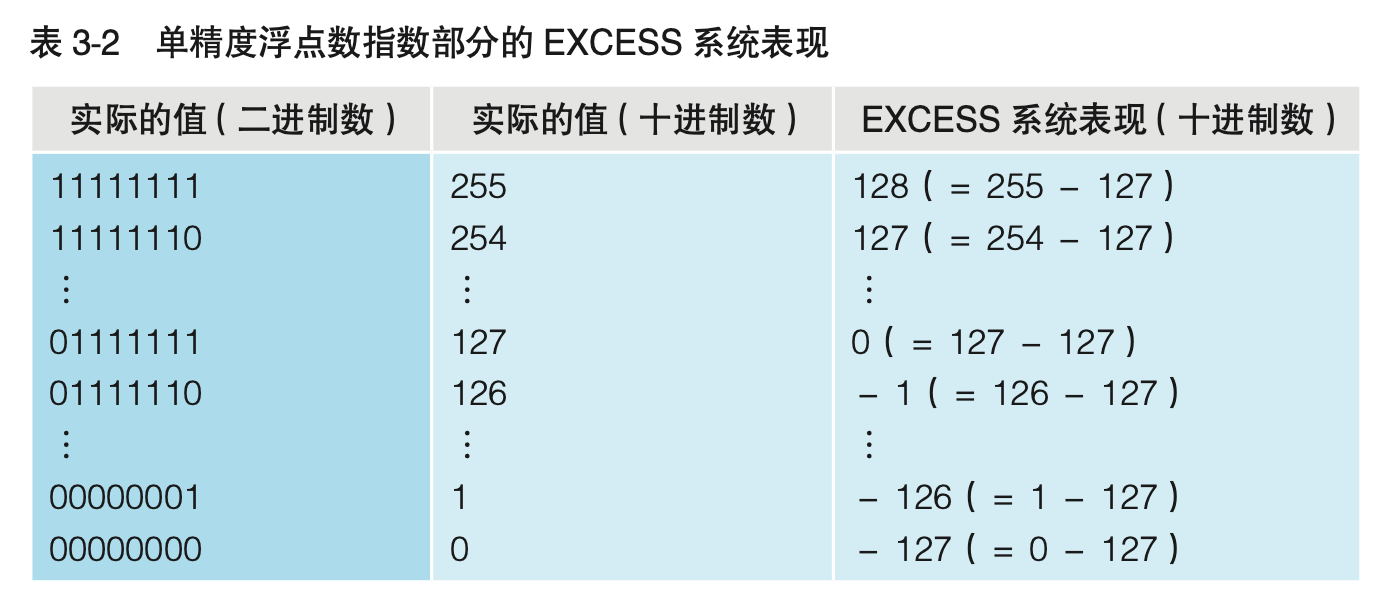
作为单精度浮点数的示例,表3-2中列出了指数部分的实际值和用EXCESS系统表现后的值。例如,指数部分为二进制数11111111(十进制数255),那么在EXCESS系统中则表示为128次幂。这是因为255-127=128。因此,8位的情况下,表示的范围就是-127次幂~128次幂。
6.在实际的程序中进行确认
如何用单精度浮点数来表示十进制数0.75?见代码清单3-2。


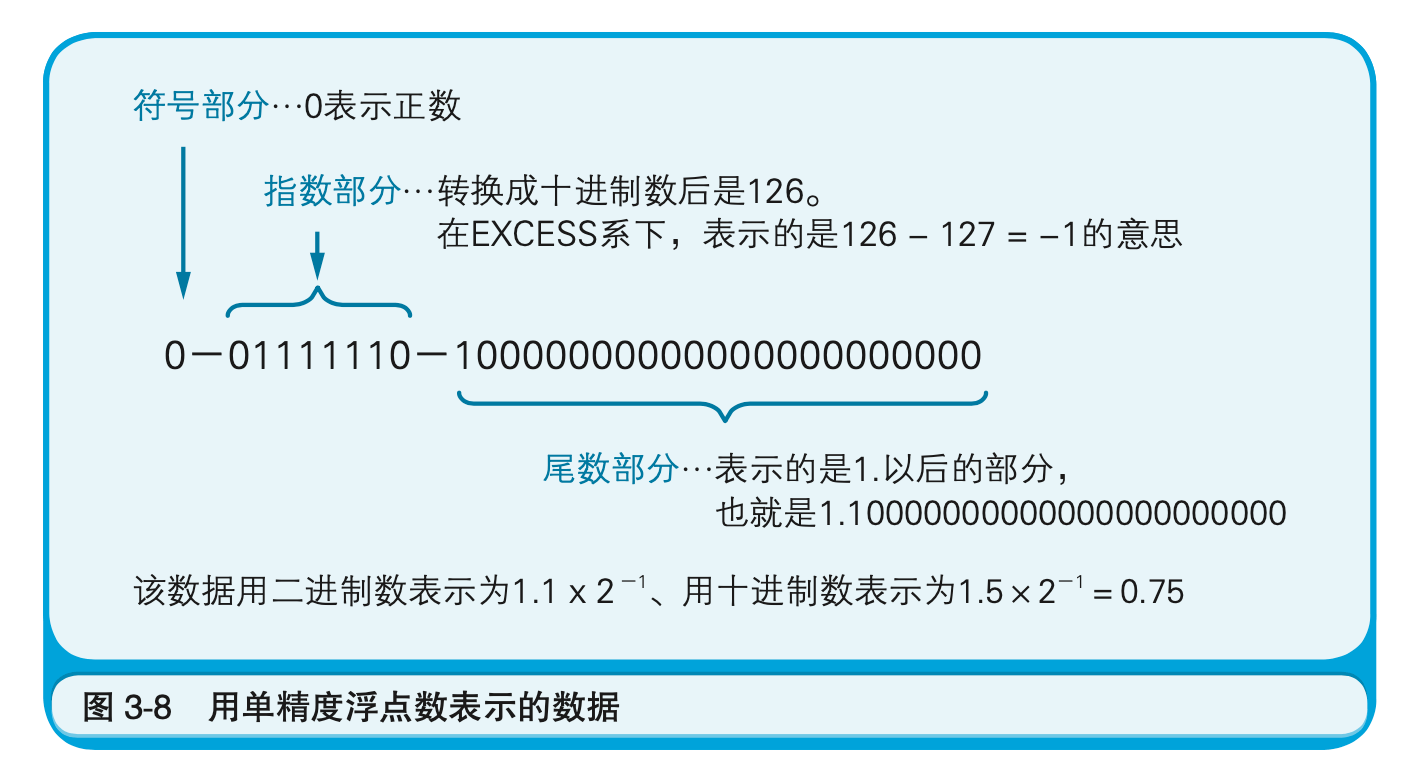
该程序执行后,十进制数0.75用单精度浮点数来表示就变成了0-01111110-10000000000000000000000(图3-7)。加入破折号(-)是为了区分符号部分、指数部分、尾数部分。因为0.75是正数,所以符号位是0。指数部分的01111110是十进制数126,用EXCESS系统表现就是-1(126-127=-1)。根据正则表达式的规则,小数点前面的第1位是1,因此尾数部分10000000000000000000000实际上表示的是1.10000000000000000000000这个二进制数。将尾数部分的二进制数转换成十进制数,结果就是(1$\times$2的0次幂)+(1$\times$2的-1次幂)=1.5。因此,0-01111110-10000000000000000000000这个单精度浮点数,表示的就是“+1.5$\times$2的-1次幂”。2的-1次幂是0.5,+1.5$\times$0.5=+0.75。正好吻合,结果正确。

接下来,我们继续使用该程序来看一下如何用单精度浮点数表示十进制数0.1。运行后就会发现结果为0-01111011-10011001100110011001101。但如果反过来计算一下这个数值的十进制数,结果并不是0.1。
7.如何避免计算机计算出错
计算机计算出错的原因之一是,采用浮点数来处理小数(另外,也有因“位溢出”而造成计算错误的情况)。作为程序的数据类型,不管是使用单精度浮点数还是双精度浮点数,都存在计算出错的可能性。接下来将介绍两种避免该问题的方法。
首先是回避策略,即无视这些错误。根据程序目的的不同,有时一些微小的偏差并不会造成什么问题。
另一个策略是把小数转换成整数来计算。计算机在进行小数计算时可能会出错,但进行整数计算(只要不超过可处理的数值范围)时一定不会出现问题。因此,进行小数的计算时可以暂时使用整数,然后再把计算结果用小数表示出来即可。例如,将0.1相加100次,就可以转换为将0.1扩大10倍后再将1相加100次的计算,最后把结果除以10就可以了(代码清单3-3)。


除此之外,BCD(Binary Coded Decimal)$^1$也是一种使用二进制表示十进制的方法。简单来讲,BCD就是用4位来表示0~9的1位数字的处理方法,这里不再做详细说明。在涉及财务计算等不允许出现误差的情况下,一定要将小数转换成整数或者采用BCD方法,以确保最终得到准确的数值。
- 计算机中用到的数据表现形式中,有一种叫作BCD(Binary Coded Decimal,二进制化十进制数)的方法。这种方法常被用于老式的大型计算机中。编程语言中,COBOL也会使用BCD。BCD分为Zone十进制数形式和Pack十进制数形式两种。
8.二进制数和十六进制数
在以位为单位表示数据时,使用二进制数很方便,但如果位数太多,看起来就比较麻烦。因此,在实际程序中,也经常会用十六进制数来代替二进制数。在C语言程序中,只需在数值的开头加上0x(0和x)就可以表示十六进制数。
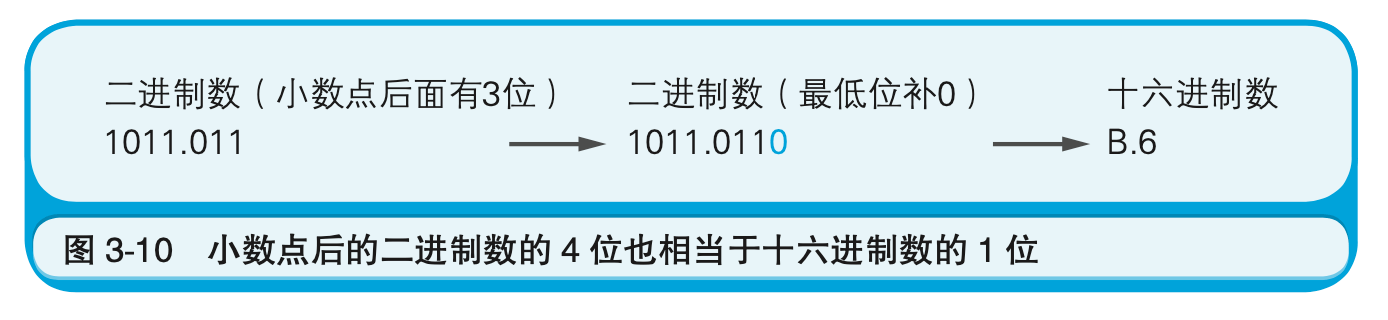
二进制数的4位,正好相当于十六进制数的1位。例如,
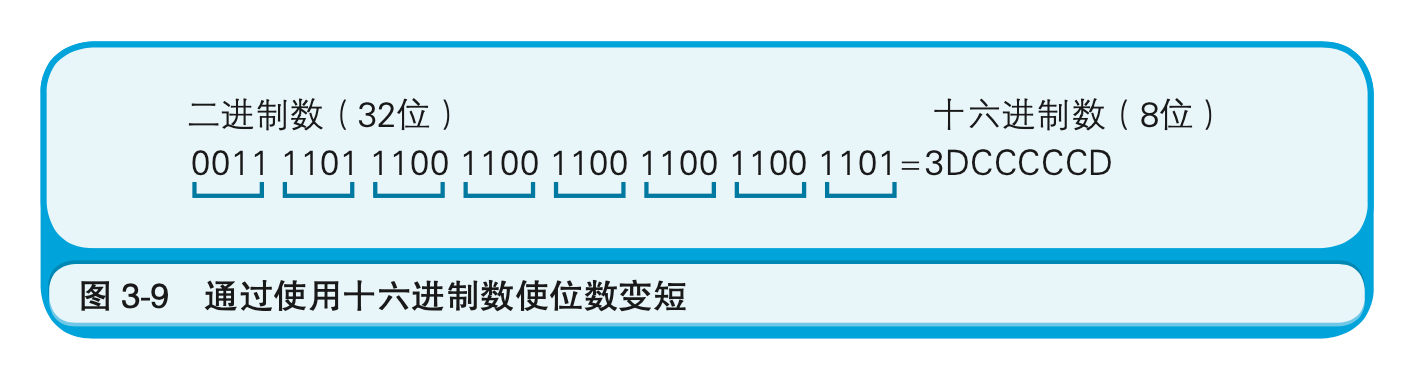
用十六进制数来表示二进制小数时,小数点后的二进制数的4位也同样相当于十六进制数的1位。不够4位时用0填补二进制数的低位即可。十六进制数的小数点后第1位的位权是$16 ^{-1}$,即0.0625。