本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.关联分析
关联规则学习(Association rule learning)是一种在大型数据库中发现变量之间的有趣性关系的方法。它的目的是利用一些有趣性的量度来识别数据库中发现的强规则。基于强规则的概念,Rakesh Agrawal等人引入了关联规则以发现由超市的POS系统记录的大批交易数据中产品之间的规律性。例如,从销售数据中发现的规则{洋葱,土豆}$\to${汉堡}会表明如果顾客一起买洋葱和土豆,他们也有可能买汉堡的肉。此类信息可以作为做出促销定价或产品植入等营销活动决定的根据。除了上面购物篮分析中的例子以外,关联规则如今还被用在许多应用领域中,包括网络用法挖掘、入侵检测、连续生产及生物信息学中。与序列挖掘相比,关联规则学习通常不考虑在事务中、或事务间的项目的顺序。
关联规则定义为:假设$I=\{ I_1,I_2,…,I_m \}$是项目的集合(项集)。给定一个交易数据库$D = \{ t_1,t_2,…,t_n\}$,其中每个交易(Transaction)$t$是$I$的子集,即$t \subseteq I$,每一个交易都与一个唯一的标识符TID(Transaction ID)对应。关联规则是形如$X \Rightarrow Y$的蕴涵式,其中$X,Y \subseteq I$且$X \cap Y = \emptyset $,$X$和$Y$分别称为关联规则的先导(antecedent或left-hand-side,LHS)和后继(consequent或right-hand-side,RHS)。关联规则$X \Rightarrow Y$在$D$中的支持度(support)是$D$中交易包含$X \cup Y$的百分比,即概率$P(X \cup Y \mid D)$;置信度(confidence)是包含$X$的交易中同时包含$Y$的百分比,即条件概率$P(Y \mid X)$。如果同时满足最小支持度阈值和最小置信度阈值,则认为关联规则是有利或有用的。这些阈值由用户或者专家设定。
比如客户购买记录如下:
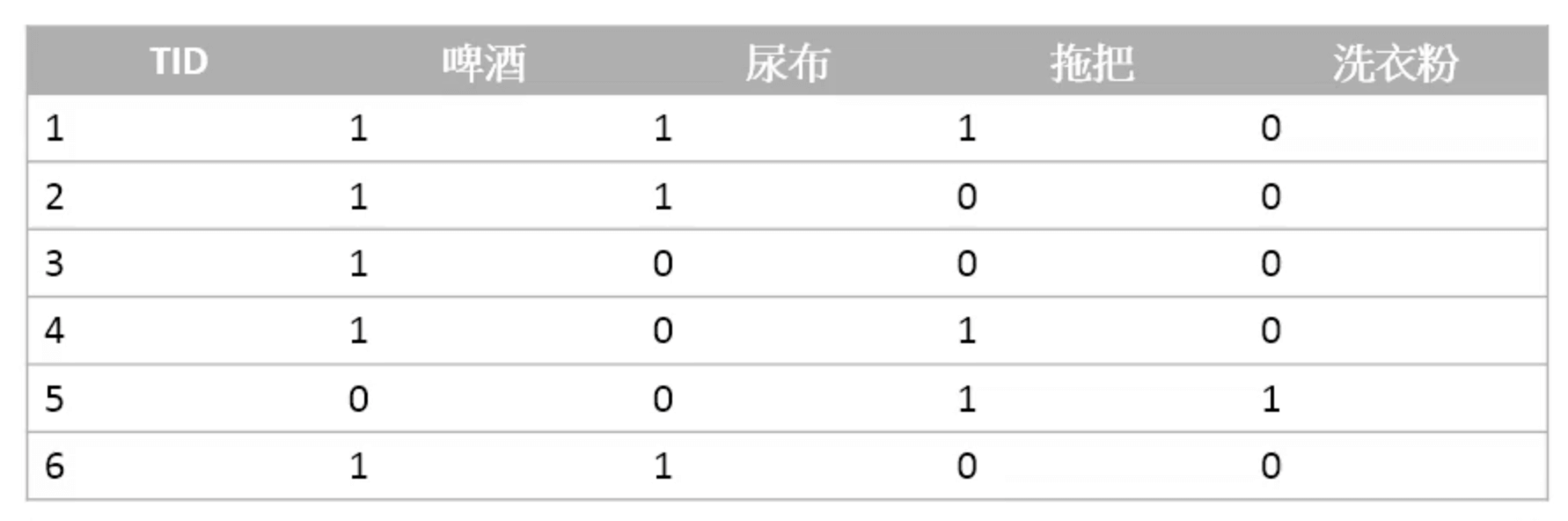
1表示购买,0表示未购买。一共有6条购买记录,其中同时购买啤酒和尿布的有3条,则支持度为$\frac{3}{6}=0.5$。在5个购买了啤酒的客户中,有3人同时也购买了尿布,则置信度为$\frac{3}{5}=0.6$。
- 一个样本称为一个“事务”。
- 每个事务由多个属性来确定,这里的属性称为“项”。
- 多个项组成的集合称为“项集”。如果某项集满足最小支持度,则称它为频繁项集。定义项集的支持度有时使用出现的频次(即相对支持度),有时使用出现的频率(即绝对支持度)。
比如,{啤酒}是1-项集;{啤酒,尿布}是2-项集;{啤酒,尿布,拖把}是3-项集。上述定义中的$X,Y$就是项集。
若关联规则$X \Rightarrow Y$的支持度和置信度分别大于或等于最小支持度阈值和最小置信度阈值,则称关联规则$X \Rightarrow Y$为强关联规则,否则称关联规则$X \Rightarrow Y$为弱关联规则。
提升度(lift):
\[\text{lift} (X \Rightarrow Y) = \frac{\text{confidence}(X \Rightarrow Y)}{\text{support}(Y)} = \frac{P(Y \mid X)}{P(B)}\]注意分母是$\text{support}(Y)$,而不是$\text{support}(X \Rightarrow Y)$。
如果提升度为1,则$X$与$Y$独立,$X$对$Y$出现的可能性没有提升作用。提升度越大($>1$),则表明$X$对$Y$的提升程度越大,也表明关联性越强。
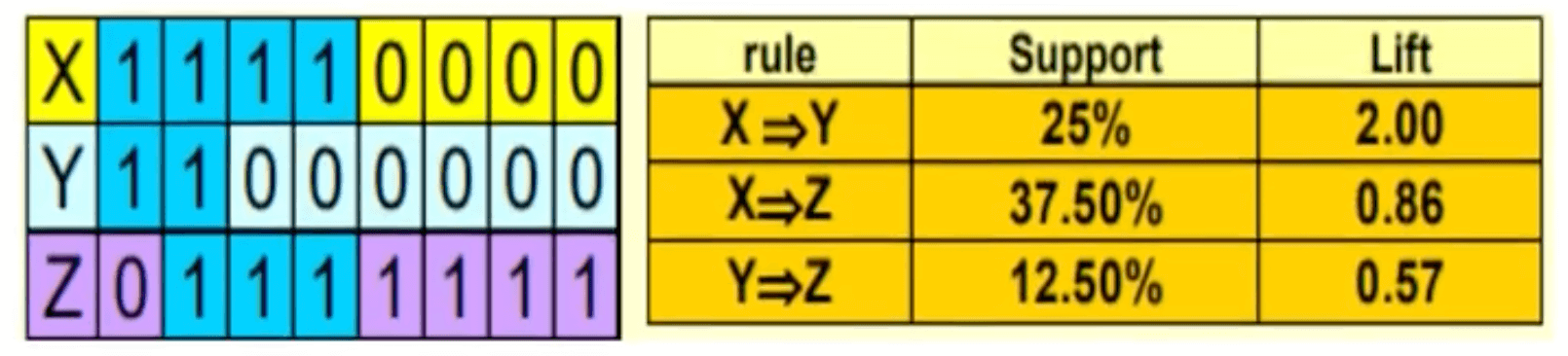
以规则$X \Rightarrow Z$为例:
\[\text{confidence}(X \Rightarrow Z) = \frac{3}{4} = 0.75\] \[\text{support}(X \Rightarrow Z) = \frac{3}{8} = 0.375\] \[\text{support}(Z) = \frac{7}{8} = 0.875\] \[\text{lift} (X \Rightarrow Z) = \frac{\text{confidence}(X \Rightarrow Z)}{\text{support}(Z) } = \frac{0.75}{0.875} \approx 0.86\]2.Apriori算法
Apriori算法是第一个关联规则挖掘算法,也是最经典的算法。它利用逐层搜索的迭代方法找出数据库中项集的关系,以形成规则,其过程由连接(类矩阵运算)与剪枝(去掉那些没必要的中间结果)组成。
Apriori算法的目的就是找到最大的K项频繁集。
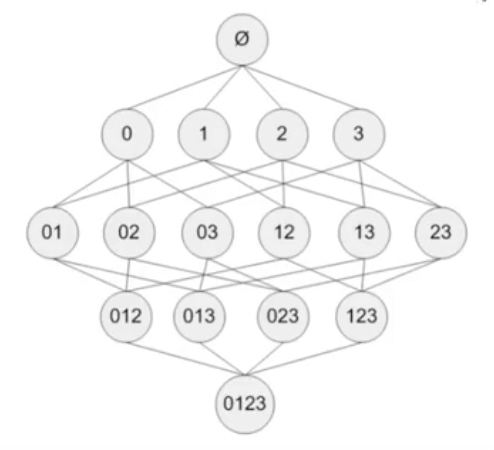
假设我们有4件商品(编号分别为0、1、2、3),我们可以组合得到的1-项集、2-项集、3-项集、4-项集如上图所示。如果我们想要找到其中的频繁项集,最简单直接的方法就是遍历所有组合,但如果我们有$n$件商品,则需要遍历$(2^n-1)$个组合,因为通常商品数量都会很多,所以这个计算成本会很高。所以Apriori算法依据以下特性对项集进行筛选:如果一个项集是非频繁项集,则它的所有超集也是非频繁的。比如项集{23}是非频繁项集,则项集{023}、{123}、{0123}都是非频繁的。
同理,如果一个项集是频繁的,则其所有的子集也都是频繁的。
Apriori算法的流程如下:
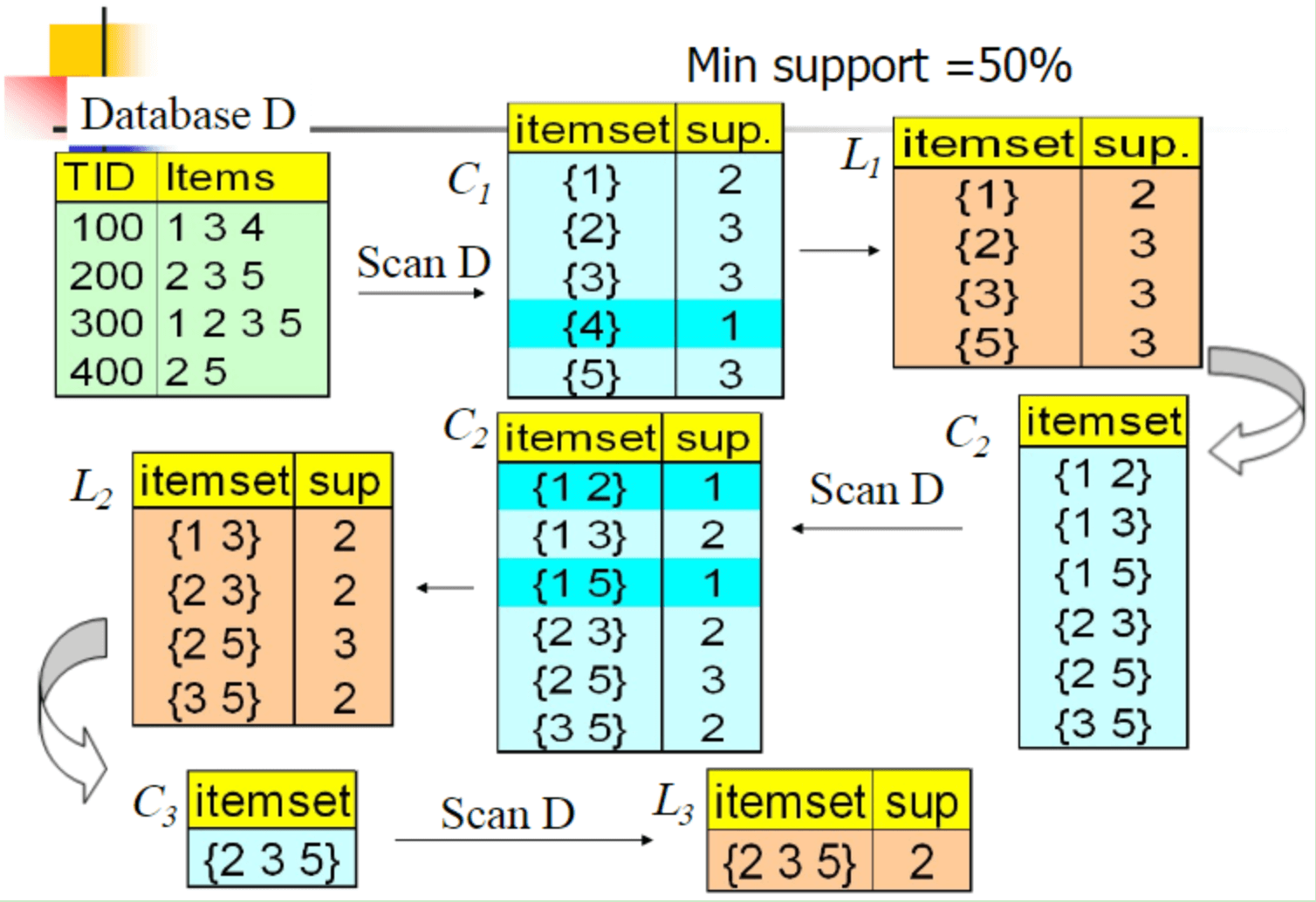
假设有4条购买记录,设置最小支持度阈值为50%,即最低出现频次为2次。首先列出所有1-项集的相对支持度,{4}的频次低于2,所以被舍弃。将剩余的1-项集组成可能的2-项集,再计算这些2-项集的相对支持度,舍弃频次低于2的{1,2}和{1,5}。同理,将剩下的2-项集组合成3-项集,并根据最小支持度阈值进行筛选。重复迭代这一过程,直到没有更大的频繁项集出现。
3.apyori
我们调用apyori库中的apriori函数来运行Apriori算法。
核心代码:
1
2
from apyori import apriori
rules = apriori(transactions, min_support=0.2, min_confidence=0.5, min_lift=3, min_length=2)
transactions是一个双层list,比如:
1
2
3
[[1, 2, 3]
[2, 5]
[3, 5, 7, 8]]
在本例中,每一个子list代表一个用户,子list中的每个元素代表该用户看过的电影(完整代码链接详见本文第4部分)。
输出频繁项集(满足最小支持度阈值),也就是哪些电影常被一起观看:
1
2
3
result = list(rules)
for rec in result:
print([item for item in rec.items])
1
2
3
4
[6874, 7438]
[5952, 7153, 1210, 260]
[1210, 2571, 1196, 1198]
...... #省略
对应的真实电影名字:
1
2
3
4
['Kill Bill: Vol. 1 (2003)', 'Kill Bill: Vol. 2 (2004)']
['Lord of the Rings: The Two Towers, The (2002)', 'Lord of the Rings: The Return of the King, The (2003)', 'Star Wars: Episode VI - Return of the Jedi (1983)', 'Star Wars: Episode IV - A New Hope (1977)']
['Star Wars: Episode VI - Return of the Jedi (1983)', 'Matrix, The (1999)', 'Star Wars: Episode V - The Empire Strikes Back (1980)', 'Raiders of the Lost Ark (Indiana Jones and the Raiders of the Lost Ark) (1981)']
...... #省略
从频繁项集中挖掘出符合要求(即满足最小置信度,最小提升度以及序列最小长度)的关联规则:
1
2
3
4
5
6
for rec in result:
left_hand = rec.ordered_statistics[0].items_base
right_hand = rec.ordered_statistics[0].items_add
l = ';'.join([movie_dic.get(item) for item in left_hand])
r = ';'.join([movie_dic.get(item) for item in right_hand])
print('{} => {}'.format(l, r))
输出为:
1
2
3
4
Kill Bill: Vol. 1 (2003) => Kill Bill: Vol. 2 (2004)
Lord of the Rings: The Two Towers, The (2002);Star Wars: Episode IV - A New Hope (1977) => Lord of the Rings: The Return of the King, The (2003);Star Wars: Episode VI - Return of the Jedi (1983)
Matrix, The (1999);Star Wars: Episode V - The Empire Strikes Back (1980) => Star Wars: Episode VI - Return of the Jedi (1983);Raiders of the Lost Ark (Indiana Jones and the Raiders of the Lost Ark) (1981)
...... #省略
对应的movieId:
1
2
3
4
[6874] => [7438] #对应第一个频繁项集
[5952, 260] => [7153, 1210] #对应第二个频繁项集
[2571, 1196] => [1210, 1198] #对应第三个频繁项集
...... #省略