【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.嵌入式选择与L1正则化
在过滤式和包裹式特征选择方法中,特征选择过程与学习器训练过程有明显的分别;与此不同,嵌入式特征选择是将特征选择过程与学习器训练过程融为一体,两者在同一个优化过程中完成,即在学习器训练过程中自动地进行了特征选择。
给定数据集$D = \{ (\mathbf{x}_1,y_1), (\mathbf{x}_2,y_2), …,(\mathbf{x}_m,y_m) \}$,其中$\mathbf{x} \in \mathbb{R}^d, y\in \mathbb{R}$。我们考虑最简单的线性回归模型,以平方误差为损失函数,则优化目标为:
\[\min_{\mathbf{w}} \sum_{i=1}^m (y_i - \mathbf{w}^T \mathbf{x}_i)^2 \tag{1}\]当样本特征很多,而样本数相对较少时,式(1)很容易陷入过拟合。为了缓解过拟合问题,可对式(1)引入正则化项。若使用$L_2$范数正则化,则有:
\[\min_{\mathbf{w}} \sum_{i=1}^m (y_i - \mathbf{w}^T \mathbf{x}_i)^2 + \lambda \parallel \mathbf{w} \parallel_2^2 \tag{2}\]其中正则化参数$\lambda > 0$。式(2)称为“岭回归”(ridge regression),通过引入$L_2$范数正则化,确能显著降低过拟合的风险。
岭回归最初由A.Tikhonov在1943年发表于《苏联科学院院刊》,因此亦称“Tikhonov回归”,而$L_2$正则化亦称“Tikhonov正则化”。
那么,能否将正则化项中的$L_2$范数替换为$L_p$范数呢?答案是肯定的。若令$p=1$,即采用$L_1$范数,则有:
\[\min_{\mathbf{w}} \sum_{i=1}^m (y_i - \mathbf{w}^T \mathbf{x}_i)^2 + \lambda \parallel \mathbf{w} \parallel_1 \tag{3}\]其中正则化参数$\lambda>0$。式(3)称为LASSO。
LASSO:Least Absolute Shrinkage and Selection Operator,直译为“最小绝对收缩选择算子”,简称为LASSO。
$L_1$范数和$L_2$范数正则化都有助于降低过拟合风险,但前者还会带来一个额外的好处:它比后者更易于获得“稀疏”(sparse)解,即它求得的$\mathbf{w}$会有更少的非零分量。
事实上,对$\mathbf{w}$施加“稀疏约束”(即希望$\mathbf{w}$的非零分量尽可能少)最自然的是使用$L_0$范数,但$L_0$范数不连续,难以优化求解,因此常使用$L_1$范数来近似。
为了理解这一点,我们来看一个直观的例子:假定$\mathbf{x}$仅有两个属性,于是无论式(2)还是式(3)解出的$\mathbf{w}$都只有两个分量,即$w_1,w_2$,我们将其作为两个坐标轴,然后在图中绘制出式(2)与(3)的第一项的“等值线”,即在$(w_1,w_2)$空间中平方误差项取值相同的点的连线,再分别绘制出$L_1$范数与$L_2$范数的等值线,即在$(w_1,w_2)$空间中$L_1$范数取值相同的点的连线,以及$L_2$范数取值相同的点的连线,如图11.2所示。式(2)与(3)的解要在平方误差项与正则化项之间折中,即出现在图中平方误差项等值线与正则化项等值线相交处。由图11.2可看出,采用$L_1$范数时平方误差项等值线与正则化项等值线的交点常出现在坐标轴上,即$w_1$或$w_2$为0,而在采用$L_2$范数时,两者的交点常出现在某个象限中,即$w_1$或$w_2$均非0;换言之,采用$L_1$范数比$L_2$范数更易于得到稀疏解。
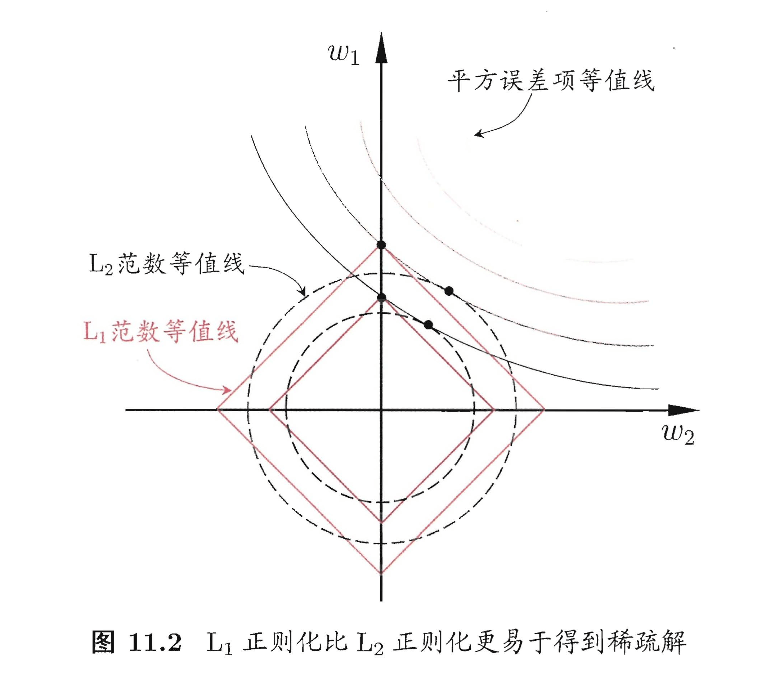
注意到$\mathbf{w}$取得稀疏解意味着初始的$d$个特征中仅有对应着$\mathbf{w}$的非零分量的特征才会出现在最终模型中,于是,求解$L_1$范数正则化的结果是得到了仅采用一部分初始特征的模型;换言之,基于$L_1$正则化的学习方法就是一种嵌入式特征选择方法,其特征选择过程与学习器训练过程融为一体,同时完成。
$L_1$正则化问题的求解可使用近端梯度下降(Proximal Gradient Descent,简称PGD)。具体来说,令$\nabla$表示微分算子,对优化目标:
\[\min_{\mathbf{x}} f(\mathbf{x}) + \lambda \parallel \mathbf{x} \parallel _1 \tag{4}\]若$f(\mathbf{x})$可导,且$\nabla f$满足L-Lipschitz条件(见本文第2部分),即存在常数$L>0$使得:
\[\parallel \nabla f(\mathbf{x}') - \nabla f(\mathbf{x}) \parallel ^2_2 \leqslant L \parallel \mathbf{x}' - \mathbf{x} \parallel ^2_2 \ (\forall \mathbf{x}, \mathbf{x'}) \tag{5}\]则在$\mathbf{x}_k$附近可将$f(\mathbf{x})$通过二阶泰勒展式近似为:
\[\begin{align} \hat{f} (\mathbf{x}) & \simeq f(\mathbf{x}_k) + \langle \nabla f(\mathbf{x}_k), \mathbf{x}-\mathbf{x}_k \rangle + \frac{L}{2} \parallel \mathbf{x} - \mathbf{x}_k \parallel ^2 \\ &= \frac{L}{2} \parallel \mathbf{x} - ( \mathbf{x}_k - \frac{1}{L} \nabla f(\mathbf{x}_k) ) \parallel _2^2 + \text{const} \end{align} \tag{6}\]其中$\text{const}$是与$\mathbf{x}$无关的常数,$\langle \cdot, \cdot \rangle$表示内积。显然,式(6)的最小值在如下$\mathbf{x}_{k+1}$获得:
\[\mathbf{x}_{k+1} = \mathbf{x}_k - \frac{1}{L} \nabla f(\mathbf{x}_k) \tag{7}\]于是,若通过梯度下降法对$f(\mathbf{x})$进行最小化,则每一步梯度下降迭代实际上等价于最小化二次函数$\hat{f}(\mathbf{x})$。将这个思想推广到式(4),则能类似地得到其每一步迭代应为:
\[\mathbf{x}_{k+1} = \arg \min_{\mathbf{x}} \frac{L}{2} \left \| \mathbf{x} - \left( \mathbf{x}_k - \frac{1}{L} \nabla f(\mathbf{x}_k) \right) \right \|_2^2 + \lambda \left \| \mathbf{x} \right \|_1 \tag{8}\]即在每一步对$f(\mathbf{x})$进行梯度下降迭代的同时考虑$L_1$范数最小化。
对于式(8),可先计算$\mathbf{z} = \mathbf{x}_k - \frac{1}{L} \nabla f (\mathbf{x}_k)$,然后求解。
\[\mathbf{x}_{k+1} = \arg \min_{\mathbf{x}} \frac{L}{2} \left \| \mathbf{x} - \mathbf{z} \right \|_2^2 + \lambda \left \| \mathbf{x} \right \| _1 \tag{9}\]令$x^i$表示$\mathbf{x}$的第$i$个分量,将式(9)按分量展开可看出,其中不存在$x^ix^j$($i \neq j$)这样的项,即$\mathbf{x}$的各分量互不影响,于是式(9)有闭式解。
\[x_{k+1}^i = \begin{cases} z^i - \lambda / L, & \lambda/L < z^i; \\ 0, & \lvert z^i \rvert \leqslant \lambda/L; \\ z^i + \lambda / L, & z^i < -\lambda / L, \end{cases} \tag{10}\]其中$x_{k+1}^i$与$z^i$分别是$\mathbf{x}_{k+1}$与$\mathbf{z}$的第$i$个分量。因此,通过PGD能使LASSO和其他基于$L_1$范数最小化的方法得以快速求解。
2.利普希茨连续
2.1.连续函数
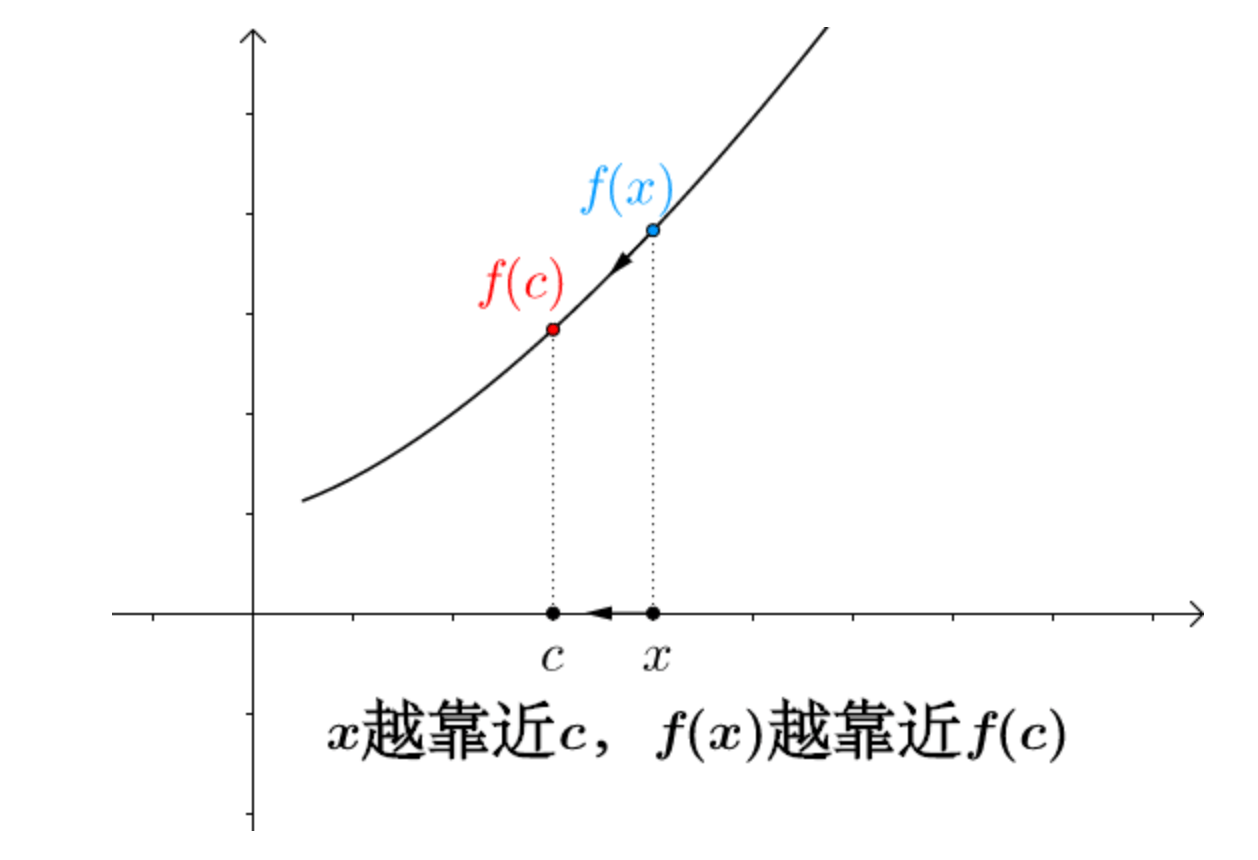
连续函数(continuous function)是指函数在数学上的属性为连续。直观上来说,连续的函数就是当输入值的变化足够小的时候,输出的变化也会随之足够小的函数。
如果输入值的某种微小的变化会产生输出值的一个突然的跳跃甚至无法定义,则这个函数被称为是不连续函数,或者说具有不连续性。非连续函数一定存在间断点。
2.2.一致连续
一致连续又称均匀连续(uniformly continuous),是比连续更苛刻的条件。
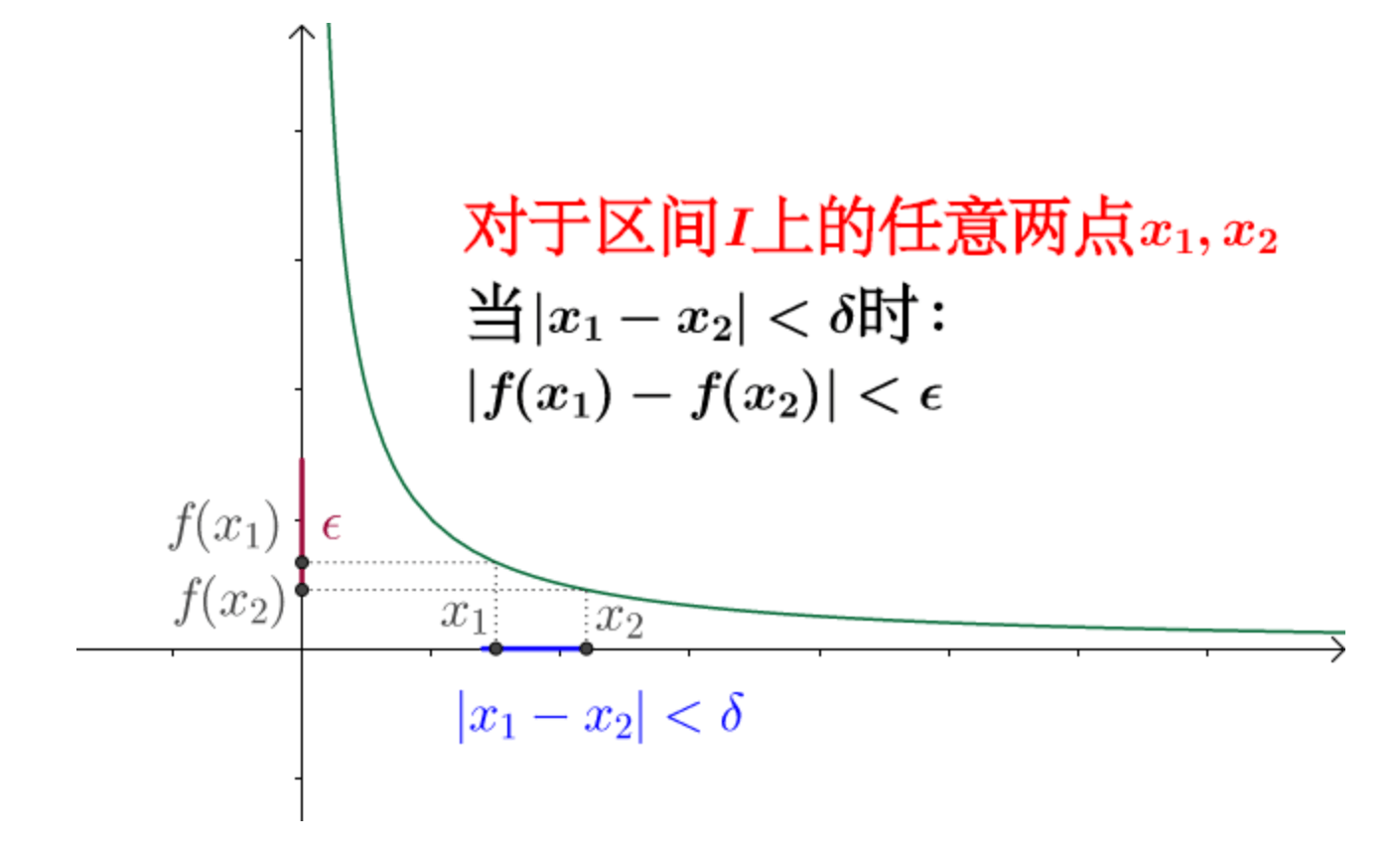
设函数$f(x)$在区间$I$上有定义,$\forall \epsilon > 0, \exists \delta > 0$,使得对于区间$I$上的任意两点$x_1,x_2$,当$\lvert x_1-x_2 \rvert < \delta$时,有$\lvert f(x_1) - f(x_2) \rvert < \epsilon$。那么称函数$f(x)$在区间$I$上一致连续。
一致连续对比连续实际上多了一个条件:
2.3.利普希茨连续
在数学中,特别是实分析,利普希茨连续(Lipschitz continuity)以德国数学家鲁道夫·利普希茨命名,是一个比一致连续更强的光滑性条件。直觉上,利普希茨连续函数限制了函数改变的速度,符合利普希茨条件的函数的斜率,必小于一个称为利普希茨常数的实数(该常数依函数而定)。
👉定义:对于在实数集的子集的函数$f : D \subseteq \mathbb{R} \to \mathbb{R}$,若存在常数$K$,使得$\lvert f(a) - f(b) \rvert \leqslant K \lvert a - b \rvert \quad \forall a,b \in D$,则称$f$符合利普希茨条件,对于$f$最小的常数$K$称为$f$的利普希茨常数。
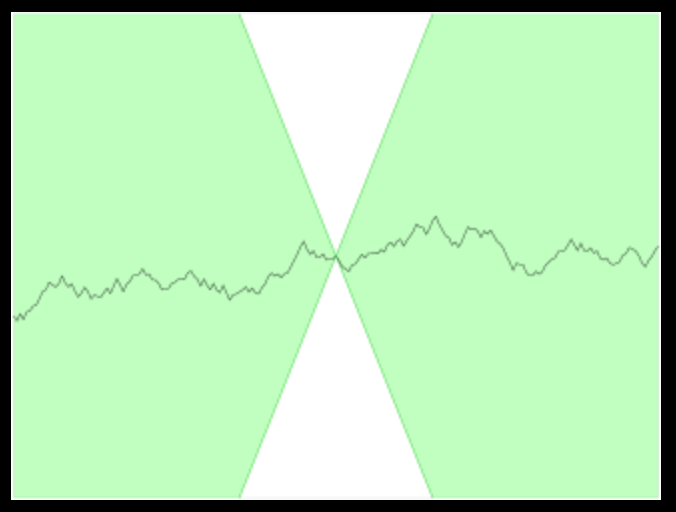
对于利普希茨连续函数,存在一个双圆锥(白色)其顶点可以沿着曲线平移,使得曲线总是完全在这两个圆锥外。
3.式(6)的推导
根据我们在wiki百科中查到的利普希茨连续的定义(见第2.3部分),式(5)应该写成:
\[\lvert \nabla f(\mathbf{x}') - \nabla f(\mathbf{x}) \rvert \leqslant L \lvert \mathbf{x}' - \mathbf{x} \rvert \quad (\forall \mathbf{x},\mathbf{x}')\]移项得:
\[\frac{\lvert \nabla f(\mathbf{x}') - \nabla f(\mathbf{x}) \rvert }{\lvert \mathbf{x}' - \mathbf{x} \rvert} \leqslant L \quad (\forall \mathbf{x},\mathbf{x}')\]由于上式对所有的$\mathbf{x},\mathbf{x}’$都成立,由导数的定义,上式可以看成是$f(\mathbf{x})$的二阶导数恒不大于$L$。即:
\[\nabla ^2 f(\mathbf{x}) \leqslant L\]由泰勒公式,$\mathbf{x}_k$附近的$f(\mathbf{x})$通过二阶泰勒展开式可近似为:
\[\begin{align} \hat{f} (\mathbf{x}) & \simeq f(\mathbf{x}_k) + \langle \nabla f(\mathbf{x}_k), \mathbf{x}-\mathbf{x}_k \rangle + \frac{\nabla ^2 f(\mathbf{x}_k)}{2} \parallel \mathbf{x} - \mathbf{x}_k \parallel ^2 \\& \leqslant f(\mathbf{x}_k) + \langle \nabla f(\mathbf{x}_k), \mathbf{x}-\mathbf{x}_k \rangle + \frac{L}{2} \parallel \mathbf{x} - \mathbf{x}_k \parallel ^2 \\&= f(\mathbf{x}_k) + \nabla f(\mathbf{x}_k)^{\top} (\mathbf{x} - \mathbf{x}_k) + \frac{L}{2} (\mathbf{x} - \mathbf{x}_k)^{\top} (\mathbf{x} - \mathbf{x}_k) \\&= f(\mathbf{x}_k) + \frac{L}{2} \left( (\mathbf{x} - \mathbf{x}_k)^{\top} (\mathbf{x} - \mathbf{x}_k) + \frac{2}{L} \nabla f(\mathbf{x}_k)^{\top} (\mathbf{x} - \mathbf{x}_k) \right) \\&= f(\mathbf{x}_k) + \frac{L}{2} \left( (\mathbf{x} - \mathbf{x}_k)^{\top} (\mathbf{x} - \mathbf{x}_k) + \frac{2}{L} \nabla f(\mathbf{x}_k)^{\top} (\mathbf{x} - \mathbf{x}_k) + \frac{1}{L^2} \nabla f(\mathbf{x}_k)^{\top} \nabla f(\mathbf{x}_k) \right) - \frac{1}{2L} \nabla f(\mathbf{x}_k)^{\top} \nabla f(\mathbf{x}_k) \\&= f(\mathbf{x}_k) +\frac{L}{2} \left( (\mathbf{x} - \mathbf{x}_k) + \frac{1}{L} \nabla f (\mathbf{x}_k) \right)^{\top} \left( (\mathbf{x} - \mathbf{x}_k) + \frac{1}{L} \nabla f (\mathbf{x}_k) \right) - \frac{1}{2L} \nabla f(\mathbf{x}_k)^{\top} \nabla f(\mathbf{x}_k) \\&= \frac{L}{2} \left \| \mathbf{x} - \left( \mathbf{x}_k - \frac{1}{L} \nabla f(\mathbf{x}_k) \right) \right \|_2^2 + \text{const} \end{align}\]$\langle … \rangle$为矩阵内积。
其中,
\[\text{const} = f(\mathbf{x}_k) - \frac{1}{2L} \nabla f(\mathbf{x}_k)^{\top} \nabla f(\mathbf{x}_k)\]4.式(10)的推导
令优化函数:
\[\begin{align} g(\mathbf{x}) &= \frac{L}{2} \left \| \mathbf{x} - \mathbf{z} \right \| _2^2 + \lambda \left \| \mathbf{x} \right \| _1 \\&= \frac{L}{2} \sum_{i=1}^d \left \| x^i - z^i \right \| _2^2 + \lambda \sum_{i=1}^d \left \| x^i \right \|_1 \\&= \sum_{i=1}^d \left( \frac{L}{2} (x^i - z^i)^2 + \lambda \lvert x^i \rvert \right) \end{align}\]这个式子表明优化$g(\mathbf{x})$可以被拆解成优化$\mathbf{x}$的各个分量的形式,对分量$x^i$,其优化函数:
\[g(x^i) = \frac{L}{2} (x^i - z^i)^2 + \lambda \lvert x^i \rvert\]求导得:
\[\frac{dg(x^i)}{dx^i} = L(x^i - z^i) + \lambda \text{sign} (x^i)\]其中:
\[\text{sign} (x^i) = \begin{cases} 1, & x^i > 0 \\ -1, & x^i < 0 \end{cases}\]称为符号函数,对于$x^i = 0$的特殊情况,由于$\lvert x^i \rvert$在$x^i = 0$处不光滑,所以其不可导,需单独讨论。令$\frac{dg(x^i)}{dx^i}=0$有:
\[x^i = z^i - \frac{\lambda}{L} \text{sign} (x^i)\]此式的解即为优化目标$g(x^i)$的极值点,因为等式两端均含有未知变量$x^i$,故分情况讨论。
1️⃣当$z^i >\frac{\lambda}{L}$时:
👉假设$x^i<0$,则$\text{sign}(x^i)=-1$,那么有$x^i = z^i + \frac{\lambda}{L} > 0$与假设矛盾。
👉假设$x^i>0$,则$\text{sign}(x^i)=1$,那么有$x^i = z^i - \frac{\lambda}{L} > 0$和假设相符合,下面来检验$x^i = z^i - \frac{\lambda}{L}$能否使函数$g(x^i)$取得最小值。当$x^i > 0$时,
\[\frac{dg(x^i)}{dx^i} = L(x^i - z^i) + \lambda\]在定义域内连续可导,则$g(x^i)$的二阶导数:
\[\frac{d^2 g(x^i)}{d{x^i}^2} = L\]由于$L$是Lipschitz常数恒大于0(此时为凸函数),因此$x^i = z^i - \frac{\lambda}{L}$是函数$g(x^i)$的最小值。
👉假设$x^i=0$,此时$g(x^i) = \frac{L}{2} (z^i)^2$,我们来比较下$x^i=0$时的$g(x^i)$和上面求得的最小值相比哪个更小。
\[\begin{align} g(x^i) \mid _{x^i = 0} - g(x^i) \mid _{x^i = z^i - \frac{\lambda}{L}} &= \frac{L}{2} (z^i)^2 - \left( \lambda z^i - \frac{\lambda^2}{2L} \right) \\& = \frac{L}{2} \left( z^i - \frac{\lambda}{L} \right)^2 \\& > 0 \end{align}\]说明$x^i = 0$并没有取得更小的值。
2️⃣当$z^i < - \frac{\lambda}{L}$时:
👉假设$x^i > 0$,则$\text{sign} (x^i) = 1$,那么有$x^i = z^i - \frac{\lambda}{L}<0$与假设矛盾。
👉假设$x^i < 0$,则$\text{sign} (x^i) = -1$,那么有$x^i = z^i + \frac{\lambda}{L} < 0$与假设相符,由上述二阶导数恒大于0可知,$x^i = z^i + \frac{\lambda}{L}$是函数$g(x^i)$的最小值。
👉假设$x^i = 0$,此时$g(x^i) = \frac{L}{2} (z^i)^2$,同样和上面求得的最小值进行比较。
\[\begin{align} g(x^i) \mid _{x^i = 0} - g(x^i) \mid _{x^i = z^i + \frac{\lambda}{L}} &= \frac{L}{2} (z^i)^2 - \left( -\lambda z^i - \frac{\lambda^2}{2L} \right) \\& = \frac{L}{2} \left( z^i + \frac{\lambda}{L} \right)^2 \\& > 0 \end{align}\]说明$x^i = 0$并没有取得更小的值。
3️⃣当$-\frac{\lambda}{L} \leqslant z^i \leqslant \frac{\lambda}{L}$时:
👉假设$x^i > 0$,则$\text{sign} (x^i) = 1$,那么有$x^i = z^i - \frac{\lambda}{L} \leqslant 0$与假设矛盾。
👉假设$x^i < 0$,则$\text{sign} (x^i) = -1$,那么有$x^i = z^i + \frac{\lambda}{L} \geqslant 0$与假设矛盾。
👉假设$x^i = 0$,对于任何$\Delta x \neq 0$有:
$\Delta x > 0$时:
\[\begin{align} g(\Delta x) &= \frac{L}{2} (\Delta x -z^i)^2 + \lambda \lvert \Delta x \rvert \\&= \frac{L}{2} \left( (\Delta x)^2 - 2\Delta x \cdot z^i + \frac{2\lambda}{L} \lvert \Delta x \rvert \right) + \frac{L}{2} (z^i)^2 \\&= \frac{L}{2} \left( (\Delta x)^2 - 2\Delta x \cdot z^i + \frac{2\lambda}{L} \Delta x \right) + \frac{L}{2} (z^i)^2 \\&= \frac{L}{2} \left( (\Delta x)^2 + 2\Delta x (\frac{\lambda}{L} - z^i) \right) + \frac{L}{2} (z^i)^2 \\& \geqslant \frac{L}{2} (\Delta x)^2 + \frac{L}{2} (z^i)^2 \\& > g(x^i) \mid _{x^i = 0} \end{align}\]$\Delta x < 0$时:
\[\begin{align} g(\Delta x) &= \frac{L}{2} (\Delta x -z^i)^2 + \lambda \lvert \Delta x \rvert \\&= \frac{L}{2} \left( (\Delta x)^2 - 2\Delta x \cdot z^i + \frac{2\lambda}{L} \lvert \Delta x \rvert \right) + \frac{L}{2} (z^i)^2 \\&= \frac{L}{2} \left( (\Delta x)^2 - 2\Delta x \cdot z^i - \frac{2\lambda}{L} \Delta x \right) + \frac{L}{2} (z^i)^2 \\&= \frac{L}{2} \left( (\Delta x)^2 - 2\Delta x (\frac{\lambda}{L} + z^i) \right) + \frac{L}{2} (z^i)^2 \\& \geqslant \frac{L}{2} (\Delta x)^2 + \frac{L}{2} (z^i)^2 \\& > g(x^i) \mid _{x^i = 0} \end{align}\]因此,$x^i = 0$是$g(x^i)$的最小值点。