本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
对于现在的密集目标检测器,仍存在以下问题:
- 在训练和推理的时候,定位质量(比如IoU分数或centerness分数)评估和分类分数的使用存在不一致:
- 在最近的一些密集检测器中,如Fig1(a)所示,其定位质量评估和分类分数在训练时是独立分开的,而在推理时则是联合起来使用的。
- 定位质量评估只使用了正样本,这种方式存在风险,因为某些不可控的原因,负样本可能得到较高的定位质量,如Fig2(a)所示,两个负样本(即Fig2(a)中的绿框)的定位质量,即IoU分数,都大于0.9,但分类分数却很低。
- bbox的表示方式不灵活。通常广泛使用的bbox表示都被视为服从目标box的Dirac delta分布(个人注解:Dirac delta分布通常被用来描述一种完全确定的情况,例如在目标检测中,bbox的坐标被假设为绝对精确的,没有任何不确定性。这意味着bbox的位置是一个精确的点,而不是分布在某个范围内的区域)。然而,这并未考虑到bbox边界的模糊性和不确定性,如Fig3所示。最近有些工作将bbox构建为高斯分布,但这种方法过于简单,无法捕捉bbox位置的真实分布。实际上,其真实分布可以更加任意和灵活,而不必像高斯函数那样对称。


为了解决上述问题,我们为bbox及其定位质量设计了新的表示方法。
- 对于定位质量表示,我们将分类分数和定位质量合并在一起,可以进行端到端的训练,并且可以在推理过程中直接使用,如Fig1(b)所示。这消除了训练和推理之间的不一致,并使得定位质量与分类分数之间的关联更强,如Fig2(b)所示。此外,训练时负样本的定位质量分数被赋为0,因此整体的定位质量预测变得更加可靠和可信。这对于密集检测器尤为有利,因为其需要对整个图像中的所有候选检测框进行排序。
- 对于bbox表示,我们通过直接学习在其连续空间上的离散化概率分布来表示bbox位置的任意分布(称为通用分布,General distribution),而不引入任何其他更强的先验知识(比如高斯分布)。因此,我们可以预测得到更可靠和准确的bbox(更详细的内容见附录)。
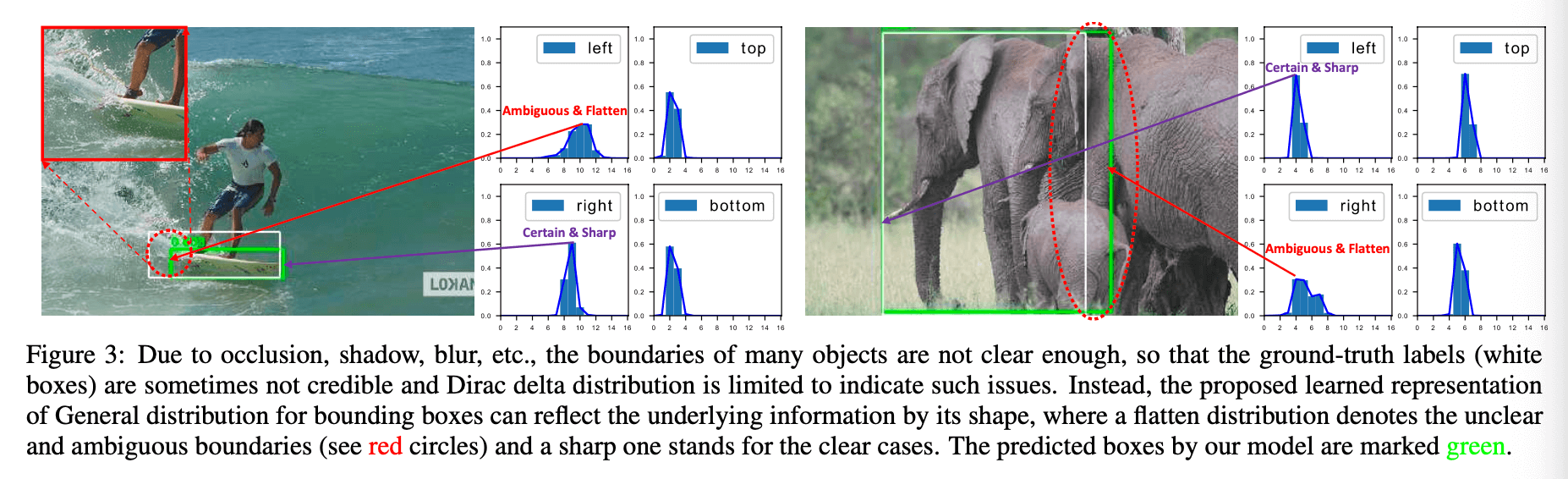
在Fig3中,由于遮挡、阴影、模糊等原因,许多目标的边界并不清晰,所以其GT box(白色框)是不可信的,Dirac delta分布无法很好的表示这种情况。绿色框是预测结果,红圈是模糊边界的区域。使用我们提出的通用分布,在Fig3左图中,可以看到,上边界、下边界和右边界都比较清晰,分布上也有明显的峰值,而对于模糊的左边界,分布上则比较平坦,没有明显的峰值。Fig3右图是一样的道理。
对于密集检测器,分类分支通常使用Focal Loss(FL)。但FL仅适用于离散的类别标签(0或1),我们将分类分数和定位质量联合在了一起,导致标签不再是离散的,而是连续的,因此,我们将FL扩展为了GFL(Generalized Focal Loss),使其可以适用于连续值。此外,GFL还可以被特例化为QFL(Quality Focal Loss)和DFL(Distribution Focal Loss)。
2.Related Work
不再详述。
3.Method
本部分我们先回顾下FL,然后详细介绍下QFL和DFL。最后将QFL和DFL统一为GFL。
\[\textbf{FL}(p)= -(1-p_t)^{\gamma} \log (p_t), \ p_t = \begin{cases} p & \text{when} \ y=1 \\ 1-p & \text{when} \ y = 0 \end{cases} \tag{1}\]这里省略了$\alpha_t$。
👉Quality Focal Loss (QFL)
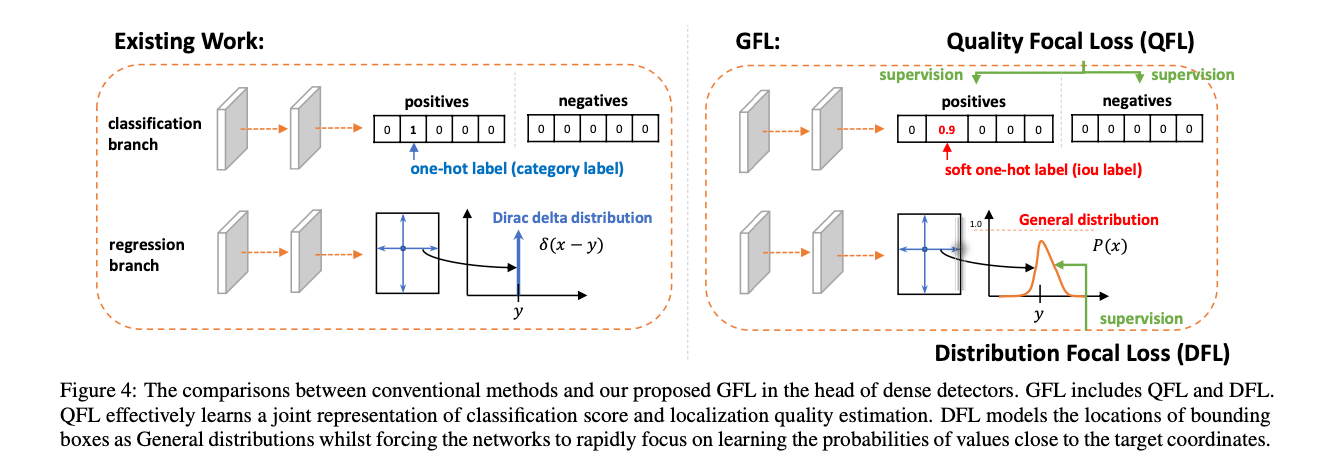
如Fig4所示,在训练阶段,对于传统方法的分类分支来说,以5分类为例,正样本的标签是形如$[0,1,0,0,0]$的one-hot编码,而负样本的标签则是$[0,0,0,0,0]$。在我们提出的方法中,正样本的标签是原有的类别标签(比如$[0,1,0,0,0]$)乘上预测bbox和GT bbox的IoU(比如0.9),即是形如$[0,0.9,0,0,0]$这样的soft one-hot编码,负样本的标签依旧是$[0,0,0,0,0]$。也就是说,在我们的方法中,训练时的软类别标签是实时算出来的,是会变化的。我们使用多个二分类来实现多分类,其中二分类使用sigmoid操作($\sigma (\cdot)$),为了简化,我们将sigmoid操作的输出记为$\sigma$(个人注解:就是类别的预测概率)。
QFL的计算公式为:
\[\textbf{QFL}(\sigma) = - \lvert y - \sigma \rvert^{\beta} \left( (1-y)\log (1-\sigma) + y\log (\sigma) \right) \tag{2}\]和FL相比,QFL做了以下2点改进:
- 交叉熵部分:因为QFL的标签$y$不再是$\{0,1 \}$形式的离散值,而是$[0,1]$范围内的连续值,所以这里用了交叉熵的完整形式:$-\left( (1-y)\log (1-\sigma) + y\log (\sigma) \right)$。
- 缩放因子部分:FL使用$(1-p_t)^{\gamma}$,而QFL将其扩展为预测值$\sigma$到连续标签$y$的绝对距离:$\lvert y - \sigma \rvert^{\beta}$。
当$\sigma = y$时,达到QFL的全局最小值。当$y=0.5$时,取不同的$\beta$值,此时QFL的变化见Fig5(a)。在我们的实验中,$\beta = 2$效果最好。

👉Distribution Focal Loss (DFL)
如Fig4所示,类似FCOS,我们使用像素点到bbox边界的距离作为回归目标,即$(l,t,r,b)$的形式。
在介绍DFL之前,先来看下Dirac delta分布。Dirac delta函数是在实数线上定义的一个广义函数或分布。它在除零以外的点上都等于零,且其在整个定义域上的积分等于1。Dirac delta函数有时可看作是在原点处无限高、无限细,但是总面积为1的一个尖峰,其示意图见下:
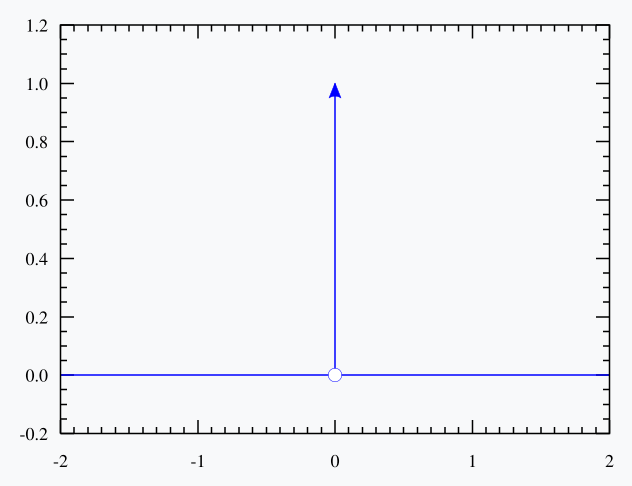
笼统地来说,Dirac delta函数是在实数线上的一个函数,在原点上无限,在所有其他点上为零:
\[\delta(x) = \begin{cases} +\infty, & x = 0 \\ 0, & x \neq 0 \end{cases}\]并同时满足以下条件:
\[\int _{-\infty}^{\infty} \delta(x)dx=1\]传统的bbox回归模型通常被视为服从Dirac delta分布:$\delta (x-y)$,其中$x$为预测值(即$(l,t,r,b)$中的某个值)的所有可能取值,$y$为对应的GT标签,且有$\int _{-\infty}^{+\infty}\delta (x-y)dx=1$(Dirac delta函数的性质)。即只有$x=y$时,$\delta$可以取到一个无穷大的值,其他时候$\delta$都是0。通俗点讲,我们只认为$x$在等于$y$的时候才是正确的,其他情况下都是错误的。但是对于bbox的模糊边界来说,$y$的定义是模糊的,所以像Dirac delta分布这种绝对的判断是不合适的,因此就有了基于高斯分布的bbox回归模型。我们可以类比一下landmark检测任务,直接回归到一个landmark坐标就属于Dirac delta分布,而回归到一个高斯heatmap就是属于高斯分布。
\[y = \int _{-\infty}^{+\infty} \delta (x-y)x dx \tag{3}\]式(3)也很好理解,因为只有$x=y$时,$\delta$才能取到值,且其积分为1。
但是我们既没用Dirac delta分布,也没用高斯分布,而是提出了一种更通用的分布$P(x)$,不需要引入任何先验。我们将标签$y$的范围定义为$y_0 \leqslant y \leqslant y_n, \ n \in \mathbb{N}^+$,那么模型的估计值$\hat{y}$(范围也为$y_0 \leqslant \hat{y} \leqslant y_n$)为:
\[\hat{y} = \int _{-\infty}^{+\infty}P(x)xdx=\int_{y_0}^{y_n}P(x)xdx \tag{4}\]个人注解:$y_0$和$y_n$可以基于目标数据集的实际分布来确定,也可以根据先验知识或经验来确定。
上式中,$x$依旧表示预测值的所有可能取值,$P(x)$为概率密度函数,式(4)(和式(3))本质上就是一个数学期望的公式,即$\hat{y}$可以理解为$x$所有可能取值的加权平均。
上式中$\hat{y}$的取值是连续的,但是在bbox回归中,$\hat{y}$的值都是以像素为单位的整数值,其范围应该是$[y_0,y_n]$的离散化表示,即$\{y_0,y_1,…,y_i,y_{i+1},…,y_{n-1},y_n \}$,其间隔为$\Delta$(为了简化,我们使用$\Delta = 1$)。因此,我们使用离散型随机变量的期望:
\[\hat{y} = \sum_{i=0}^{n} P(y_i)y_i \tag{5}\]其中,$P(x)$可以通过一个包含$n+1$个神经元的softmax层($S(\cdot)$)来实现,我们将$P(y_i)$记为$S_i$。$\hat{y}$可以和传统的损失函数(比如SmoothL1、IoU Loss、GIoU Loss)一起进行端到端的训练。然而,$P(x)$的值组合是无限的,这可能导致总能找到一些可能的组合使得最终积分得到的$\hat{y}$等于$y$,这会降低学习效率(个人注解:模型也难以收敛并且泛化性不好)。从直觉上讲,与Fig5(b1)和Fig5(b2)相比,Fig5(b3)的分布是紧凑的,并且在bbox估计上更具信心和精确性,这促使我们将Fig5(b3)的分布形状优化为在越接近$y$的地方概率值越高。此外,通常情况下,最合适的潜在位置(如果该位置存在的话)不会远离标签$y$(由于模糊或遮挡等原因,这个标签可能是粗略的)。因此,我们引入DFL(Distribution Focal Loss),通过显式地增大$y_i$和$y_{i+1}$(最接近$y$的两个值,有$y_i \leqslant y \leqslant y_{i+1}$)的概率,强制网络快速聚焦到接近标签$y$的值上。由于bbox的学习只针对正样本,所以没有类别不平衡的问题,我们仅使用完整的交叉熵损失来定义DFL:
\[\textbf{DFL} (S_i,S_{i+1}) = -\left( (y_{i+1}-y)\log (S_i) + (y-y_i)\log (S_{i+1}) \right) \tag{6}\]直观上来说,DFL的目标就是增加$y$周围值($y_i$和$y_{i+1}$)的概率。DFL的全局最小值解为$S_i = \frac{y_{i+1}-y}{y_{i+1}-y_i},S_{i+1} = \frac{y-y_i}{y_{i+1}-y_i}$(详见附录),可以保证$\hat{y}$无限接近于$y$,即:
\[\hat{y}=\sum_{j=0}^n P(y_j)y_j = S_iy_i+S_{i+1}y_{i+1} = \frac{y_{i+1}-y}{y_{i+1}-y_i}y_i + \frac{y-y_i}{y_{i+1}-y_i} y_{i+1} = y\]这也确保了它作为损失函数的正确性。
👉Generalized Focal Loss (GFL).
QFL和DFL可被统一表示为GFL(Generalized Focal Loss)。给定两个变量$y_l,y_r(y_l < y_r)$,其对应的预测概率为$p_{y_l},p_{y_r}(p_{y_l}\geqslant 0,p_{y_r} \geqslant 0, p_{y_l} + p_{y_r}=1)$,最终的预测结果为它们的线性组合:$\hat{y}=y_l p_{y_l} + y_r p_{y_r} (y_l \leqslant \hat{y} \leqslant y_r)$。预测结果$\hat{y}$对应的连续型标签$y$也满足$y_l \leqslant y \leqslant y_r$。绝对距离$\lvert y - \hat{y} \rvert^{\beta}(\beta \geqslant 0)$作为调节因子,GFL可表示为下式:
\[\textbf{GFL} (p_{y_l},p_{y_r}) = -\lvert y-(y_l p_{y_l} + y_r p_{y_r}) \rvert^{\beta} \left( (y_r -y) \log (p_{y_l})+(y-y_l)\log (p_{y_r}) \right) \tag{7}\]👉Properties of GFL.
当$p^*_{y_l} = \frac{y_r - y}{y_r - y_l},p^*_{y_r} = \frac{y- y_l}{y_r - y_l}$时,$\textbf{GFL}(p_{y_l},p_{y_r})$达到全局最小值,此时$\hat{y}$完美匹配$y$,即$\hat{y}=y_l p^*_{y_l}+y_r p^*_{y_r}=y$(证明见附录)。FL、QFL、DFL都是GFL的特例(详见附录)。GFL可应用于任何单阶段检测器。原始检测器只需要做两方面的修改。第一方面,在推理阶段,我们直接使用分类分数(联合定位质量)作为NMS分数,无需再乘以任何单独的定位质量预测(比如FCOS和ATSS中的centerness)。第二方面,用于预测每个bbox位置的回归分支的最后一层从一个输出改为$n+1$个输出(个人注解:针对$(l,t,r,b)$中的某一个值),如表3所示,这几乎没有额外的计算成本。
👉Training Dense Detectors with GFL.
GFL的训练loss定义如下:
\[\mathcal{L}=\frac{1}{N_{pos}}\sum_z \mathcal{L}_{\mathcal{Q}}+\frac{1}{N_{pos}}\sum_z \mathbf{1}_{\{c_z^*>0\}}\left( \lambda_0 \mathcal{L}_{\mathcal{B}}+\lambda_1 \mathcal{L}_{\mathcal{D}} \right) \tag{8}\]其中,$\mathcal{L}_{\mathcal{Q}}$表示QFL,$\mathcal{L}_{\mathcal{D}}$表示DFL。$\mathcal{L}_{\mathcal{B}}$表示GIoU Loss。$N_{pos}$表示阳性样本的数量。$\lambda_0$默认为2,$\lambda_1$实际上是$\frac{1}{4}$,即四个方向的平均(个人注解:$(l,t,r,b)$中的每个值都要计算DFL,且权重都是$\frac{1}{4}$)。$z$表示特征金字塔中的所有位置。$c^*_z$表示在位置$z$处的目标类别标签,当$c^*_z>0$时,表示在该位置存在一个正样本,此时$\mathbf{1}_{\{c_z^*>0\}}$等于1,如果不满足$c^*_z>0$,则表示该位置不存在正样本,此时$\mathbf{1}_{\{c_z^*>0\}}$等于0。
4.Experiment
我们实验基于COCO benchmark,训练集为trainval35k(115K张图像),验证集使用minival(5K张图像)。验证集用于消融实验。实验结果基于test-dev(20K张图像)。为了公平比较,所有结果都使用了mmdetection的默认参数。除非特殊声明,训练默认使用1x learning schedule(即12个epoch),不使用multi-scale,backbone为ResNet-50。更多训练/测试细节见附录。
我们首先验证了QFL的有效性,见表1。

表1(a)中的模型结构见Fig6:

其次,我们验证了DFL的有效性,见表2:

在表2中,为了快速选择一个合适的$n$,我们根据COCO trainval35k数据集,统计了ATSS所用的所有训练样本的回归目标(即$(l,t,r,b)$),见Fig5(c),这样我们就能知道怎么设置合理的$y_0$和$y_n$了。
通过表2我们可以发现,结果对$n$的选择并不敏感,$\Delta$建议选小一点(比如1)。
定性比较见Fig7(更多讨论见附录):

从Fig7可以看出,相比高斯分布和Dirac delta分布,通用分布的效果更好,尤其是在有遮挡的情况下。为了阐述通用分布的有效性,如Fig3所示,我们列出了2个典型例子的bbox在4个方向上的分布,能看到,通用分布的形状可以很好的反映出bbox边界的不确定性(更多细节见附录)。
在ATSS(backbone为ResNet-50)上的消融实验见表3,使用单块GeForce RTX 2080Ti GPU,batch size=1,使用一样的mmdetection框架。
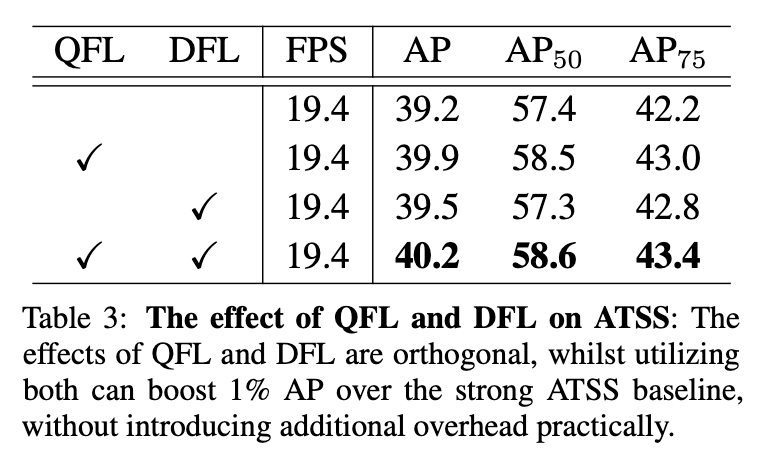
最后,我们比较了GFL(基于ATSS)和其他SOTA方法在COCO test-dev上的性能,见表4。
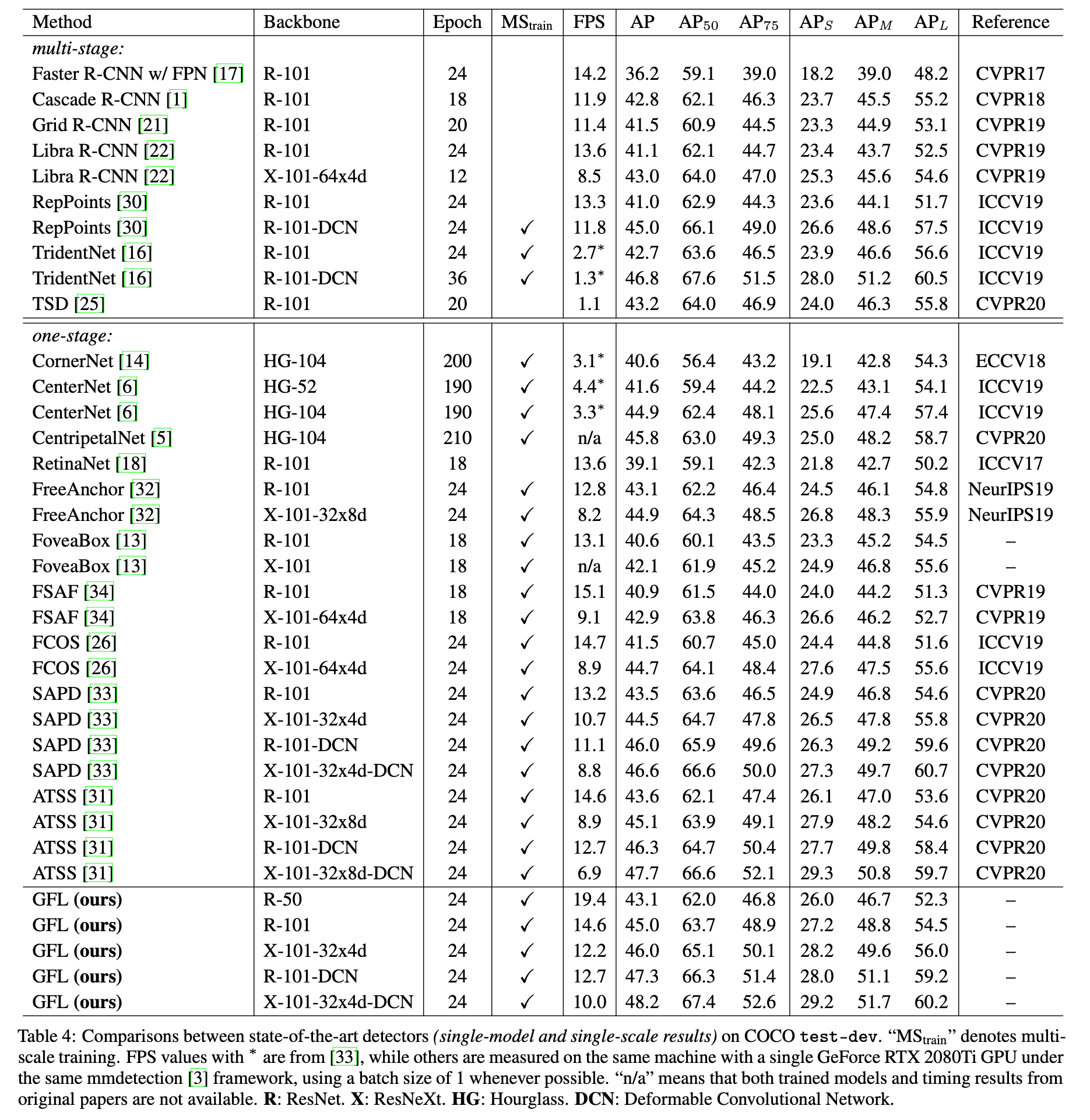
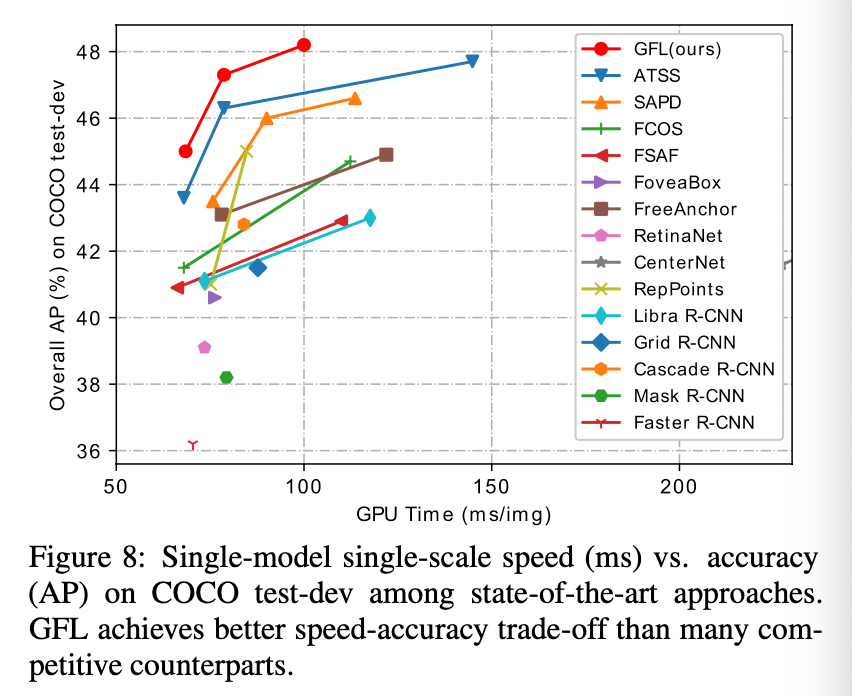
精度和速度的trade-off见Fig8:
5.Conclusion
GFL将原始FL从$\{ 0,1\}$的离散形式扩展到连续形式。GFL可以细化为QFL和DFL,其中QFL可以学到更好的分类和定位质量的联合表征,而DFL则通过通用分布来提供更具信息量且更精确的bbox预测。
6.Supplementary Materials
6.A.More Discussions about the Distributions
Dirac delta分布、高斯分布和我们提出的通用分布的比较见Fig9:
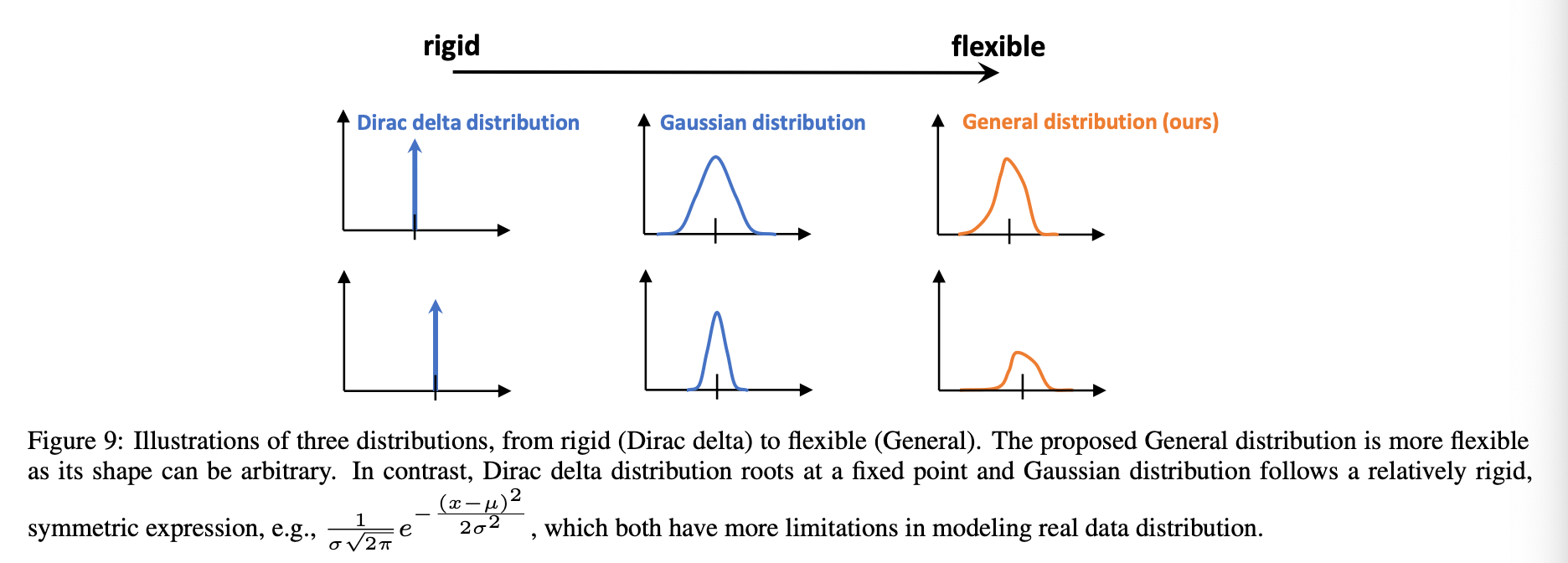
这些分布的一些关键对比见表5:

此外,我们还发现Dirac delta分布和高斯分布对特征扰动(feature perturbations)更为敏感,这使得它们鲁棒性较差且容易受到噪声的影响,如Fig10所示,GFL更稳定且对扰动不敏感。

6.B.Global Minimum of GFL
GFL全局最小值的求解过程,不再详述。
6.C.FL, QFL and DFL are special cases of GFL
本部分展示如何将GFL特例化为FL、QFL和DFL。
👉将GFL特例化为FL:
使$\beta=\gamma,y_l=0,y_r=1,p_{y_r}=p,p_{y_l}=1-p$且有$y \in \{0,1 \}$,则有:
\[\begin{align} \textbf{FL}(p) &= \textbf{GFL}(1-p,p) \\&= -\lvert y-p \rvert^{\gamma} \left( (1-y) \log (1-p) + y \log (p) \right), y \in \{0,1 \} \\&= -(1-p_t)^{\gamma} \log (p_t), p_t = \begin{cases} p, & \text{when } y =1 \\ 1-p, & \text{when } y = 0 \end{cases} \end{align} \tag{9}\]👉将GFL特例化为QFL:
使$y_l=0,y_r=1,p_{y_r}=\sigma,p_{y_l}=1-\sigma$,则有:
\[\textbf{QFL}(\sigma) = \textbf{GFL} (1-\sigma,\sigma) = -\lvert y - \sigma \rvert^{\beta} \left( (1-y)\log (1-\sigma)+y\log (\sigma) \right) \tag{10}\]👉将GFL特例化为DFL:
使$\beta=0,y_l=y_i,y_r=y_{i+1},p_{y_l}=P(y_l)=P(y_i)=S_i,p_{y_r}=P(y_r)=P(y_{i+1})=S_{i+1}$,则有:
\[\textbf{DFL}(S_i,S_{i+1})=\textbf{GFL}(S_i,S_{i+1})=-\left( (y_{i+1}-y)\log (S_i) + (y-y_i)\log (S_{i+1}) \right) \tag{11}\]6.D.Details of Experimental Settings
👉训练细节:
backbone在ImageNet上预训练。在训练期间,输入图像resize到短边为800,长边小于等于1333。在消融实验中,网络训练使用SGD,共训练90K次迭代(记为1x schedule),momentum=0.9,weight decay=0.0001,batch size=16。初始学习率为0.01,并在第60K和第80K次迭代时缩小10倍。
👉推理细节:
在推理阶段,输入图像的resize和训练阶段一样,然后通过整个网络得到预测的bbox和对应的预测类别。使用0.05的阈值过滤掉背景,每个特征金字塔输出前1000个候选检测。每个类别的NMS阈值设为0.6,最终每个图像输出前100个检测作为结果。
6.E.Why is IoU-branch always superior than centerness-branch?
作者发现IoU分支的表现要比centerness分支要好,并在本部分解释了原因。如Fig11所示,centerness分支得到的标签可能会很小,从而导致其在NMS中被抑制,最终造成漏检。而IoU分支得到的标签就大很多,不存在这个问题。

Fig12列出了centerness分支和IoU分支标签值的分布情况,可以看到centerness分支的标签值整体小很多。
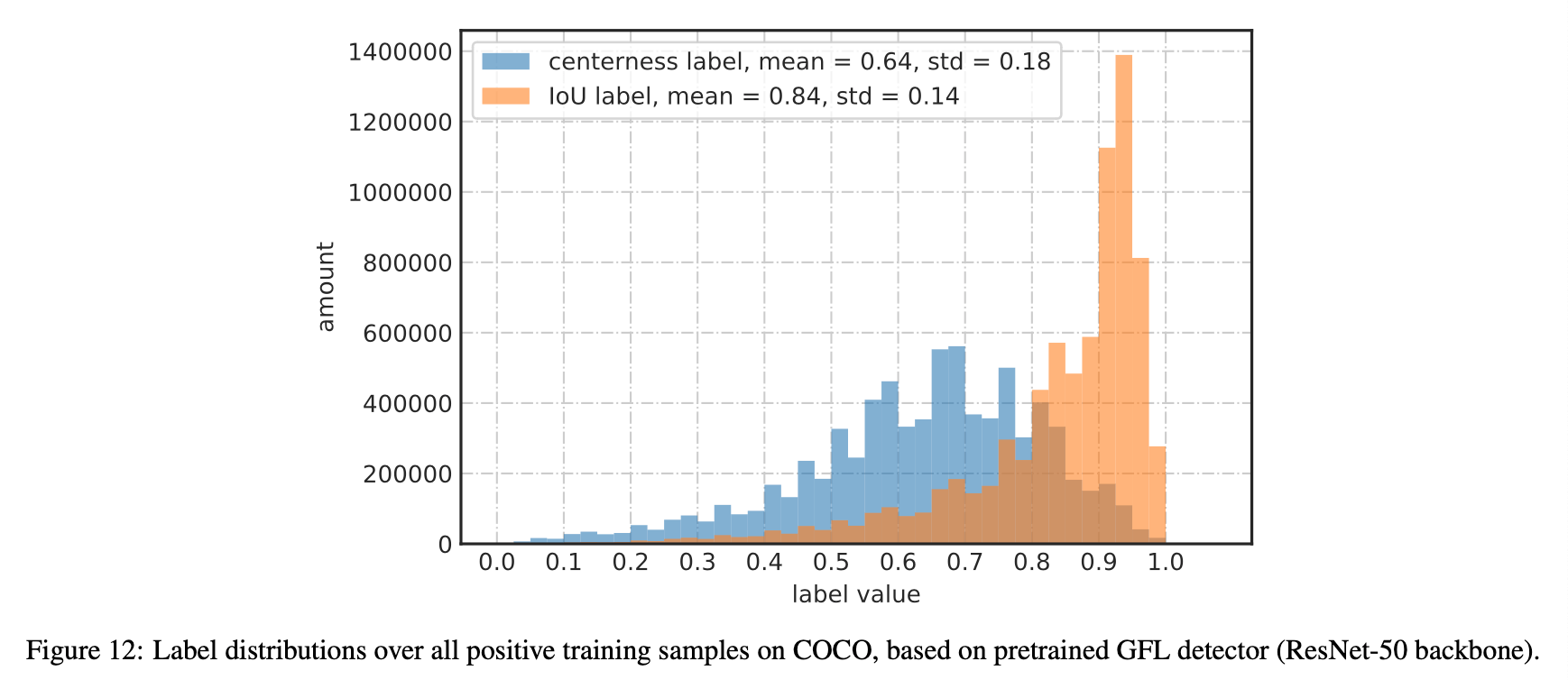
个人注解:个人不太赞同作者这里的分析,因为FCOS就是想通过centerness来排除远离目标中心位置的低质量的预测bbox。
6.F.More Examples of Distributed Bounding Boxes
本部分我们展示了使用GFL(使用ResNet-50作为backbone)预测的通用分布bbox的更多示例。在Fig13中,我们展示了几个存在模糊边界的示例:
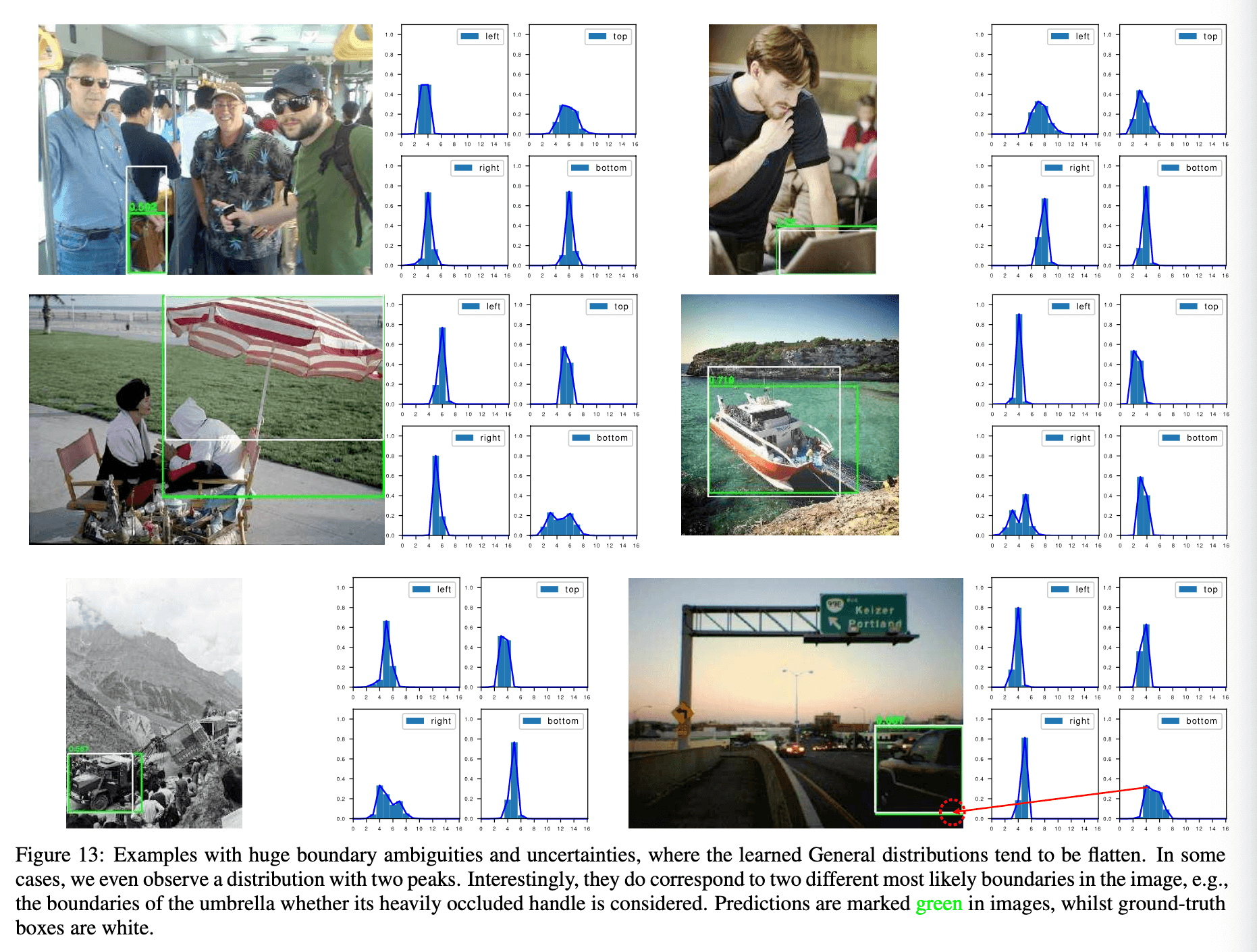
我们的模型甚至生成了比GT bbox更合理的bbox。在Fig13中,模糊边界学到的分布较为平坦,有趣的是,在雨伞的示例中,模糊边界对应的分布有两个峰值,其确实对应图像中两个不同的最可能边界。在Fig13中,白色框为GT bbox,绿色框为预测bbox。
更多边界清晰的示例见Fig14:

从Fig14可以看到,对于清晰的边界,GFL生成的通用分布相对尖锐,说明GFL非常自信生成了准确的bbox。
7.原文链接
👽Generalized Focal Loss:Learning Qualified and Distributed Bounding Boxes for Dense Object Detection