本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
源码地址:EfficientNet。
扩展(scaling up)卷积神经网络被广泛用于提高模型性能。最常见的扩展方法是增加卷积神经网络的深度和宽度。还有一种少见但日益流行的方法是通过提高图像分辨率来扩展模型。在以往的研究中,通常只采用3种扩展方法中的一种即可,同时使用多种扩展方法反倒可能导致次优的结果。
本文提出了一种简单而有效的复合扩展方法。与传统做法不同,我们的方法通过一组固定的扩展系数,统一的扩展网络的宽度、深度和分辨率。举个例子,如果我们想使用$2^N$倍的计算资源,我们可以直接将网络的深度增加$\alpha^N$倍、宽度增加$\beta^N$倍、图像大小增加$\gamma^N$倍。其中,$\alpha,\beta,\gamma$是在原有小模型基础上通过小范围网格搜索确定的固定系数。Fig2展示了我们提出的复合扩展方法和传统方法的不同,Fig2(b)-(d)是传统的扩展方法,只从一个维度进行扩展,Fig2(e)是我们提出的复合扩展方法,从三个维度同时进行扩展。

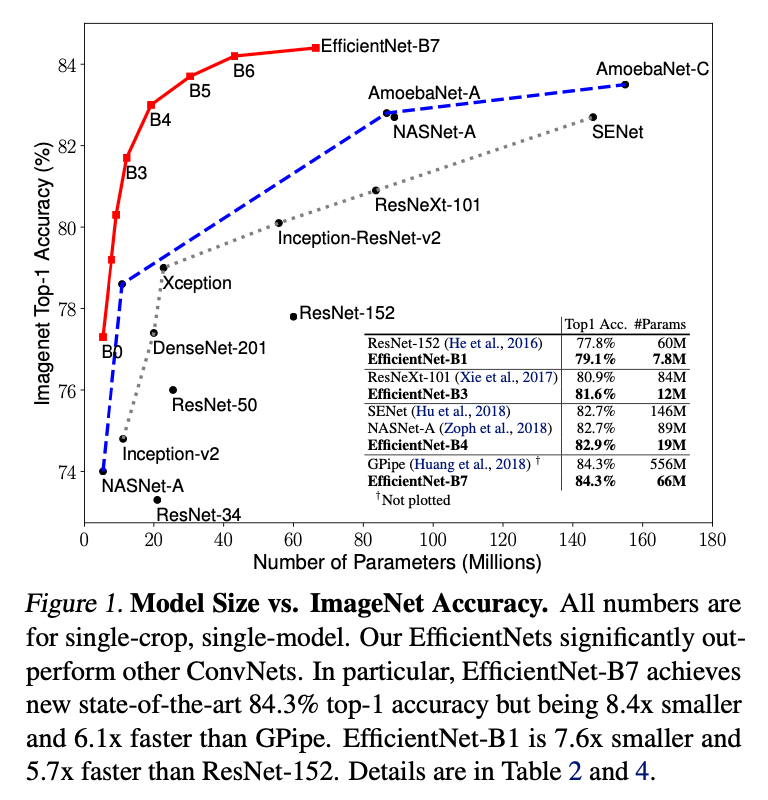
我们证明了我们的扩展方法可以在MobileNets和ResNet上表现良好。需要注意的是,扩展的效果很大程度上依赖于baseline网络,因此,我们使用神经框架搜索(neural architecture search)开发了一个新的baseline网络,并通过扩展该网络得到一系列模型,称为EfficientNets。Fig1是不同方法在ImageNet上的性能比较。
2.Related Work
不再详述。
3.Compound Model Scaling
3.1.Problem Formulation
我们可以将卷积网络的层$i$定义为函数:$Y_i = \mathcal{F}_i (X_i)$,其中$\mathcal{F}_i$是操作子,$Y_i$是输出张量,$X_i$是输入张量,其张量维度为$\langle H_i,W_i,C_i \rangle$(为了简化,省略了batch维度),其中$H_i$和$W_i$是空间维度,$C_i$是通道维度。卷积网络$\mathcal{N}$可以看作是一系列层的组合:$\mathcal{N}=\mathcal{F}_k \odot \cdots \odot \mathcal{F}_2 \odot \mathcal{F}_1(X_1) = \odot_{j=1…k}\mathcal{F}_j(X_1)$。通常情况下,卷积网络的层会被分为多个阶段,每个阶段内的所有层共享相同的结构。举个例子,ResNet有5个阶段,每个阶段内的所有层有着相同的卷积类型(除了第一层用于执行下采样)。因此,我们进一步将卷积网络定义为:
\[\mathcal{N} = \bigodot_{i=1...s} \mathcal{F}_i^{L_i} ( X_{\langle H_i , W_i , C_i \rangle} ) \tag{1}\]其中,$\mathcal{F}_i^{L_i}$表示在阶段$i$中层$\mathcal{F}_i$重复了$L_i$次,$\langle H_i , W_i , C_i \rangle$是层$i$的输入张量$X$的维度。Fig2(a)是一个典型的卷积网络,空间维度逐层减小,而通道维度逐层加大,例如,初始输入维度为$\langle 224,224,3 \rangle$,最终输出维度为$\langle 7,7,512 \rangle$。
常规的卷积网络设计通常聚焦于找到最优的层结构$\mathcal{F}_i$,与之不同的是,模型扩展是在不改变baseline网络层结构的基础上,尝试去扩展网络的长度$L_i$、宽度$C_i$和分辨率$(H_i,W_i)$。但对于每一层仍然存在一个巨大的设计空间,即我们可以探索很多不同的$L_i,C_i,H_i,W_i$。为了进一步缩小设计空间,我们限制所有层必须按照固定的比例进行统一扩展。我们的目标是在给定的资源限制条件下,最大化模型精度,这可以通过一个优化问题来表述:
\[\begin{align} \max_{d, w, r} \quad & \text{Accuracy}(\mathcal{N}(d, w, r)) \\ \text{s.t.} \quad & \mathcal{N}(d, w, r) = \bigodot_{i=1 \ldots s} \hat{\mathcal{F}}_i^{d\cdot \hat{L}_i} \left( X_{\langle r \cdot \hat{H}_i, r \cdot \hat{W}_i, w \cdot \hat{C}_i \rangle} \right) \\ & \text{Memory}(\mathcal{N}) \leq \text{target_memory} \\ & \text{FLOPS}(\mathcal{N}) \leq \text{target_flops} \end{align} \tag{2}\]其中,$w,d,r$是扩展系数。$\hat{\mathcal{F}_i},\hat{L}_i,\hat{H}_i,\hat{W}_i,\hat{C}_i$是baseline网络预定义的参数,例子见表1。

3.2.Scaling Dimensions
第二个问题的难点在于确定最优的$d,w,r$,因为$d,w,r$彼此依赖,并且在不同资源限制下,这些值会发生变化。由于这一难点,传统方法大多选择只在一个维度上扩展卷积网络。
👉Depth(d):
扩展网络深度是许多卷积网络最常用的方法。直觉上来说,更深的卷积网络能够捕获更丰富和更复杂的特征,并且在新任务上有较好的泛化性。但是,更深的网络也因梯度消失问题而难以训练。尽管一些技术,比如skip connections和batch normalization,缓解了训练问题,但随着网络的加深,准确率的收益越来越低:比如,ResNet-1000虽然更深,但其准确率和ResNet-101相似。Fig3中间的图也印证了这一结论。

👉Width(w):
对于较小的模型,扩展网络宽度(即增加通道数)是一种常见的方法。更宽的网络往往能够捕获更细粒度的特征,并且更容易训练。但是,过宽且较浅的网络难以捕获高层次的特征。从Fig3左图可以看出,当网络变得非常宽时(即$w$较大时),准确率很快就饱和了。
👉Resolution(r):
更高分辨率的输入图像能够使网络捕获更细粒度的信息。如Fig3右图所示,更高的分辨率确实可以提升准确率,但当分辨率非常高时,准确率的增益会逐渐减弱($r=1.0$表示分辨率为$224 \times 224$,$r=2.5$表示分辨率为$560 \times 560$)。
👉Observation 1
综上,我们的第一个发现是,无论扩展网络宽度、深度、分辨率中的哪个维度,准确率都可以得到提升,但随着模型越来越大,准确率的增益也越来越小。
3.3.Compound Scaling
我们通过实验观察到,不同维度的扩展并不是相互独立的。直观来说,对于更高分辨率的图像,我们应该增加网络深度,这样可以有更大的感受野。此外,当分辨率更高时,我们也应该增加网络的宽度,这样能够捕获更细粒度的信息。因此,我们应该协调和平衡不同维度的扩展,而不是单一的只扩展某一维度。
为了验证我们的猜测,我们在不同网络深度和分辨率下,比较了宽度扩展的效果,结果见Fig4。如果我们不改变深度($d=1.0$)和分辨率($r=1.0$),只扩展宽度,准确率很快就饱和了。但如果增加深度($d=2.0$)和分辨率($r=2.0$),在相同FLOPS下,扩展宽度可以得到更高的准确率。
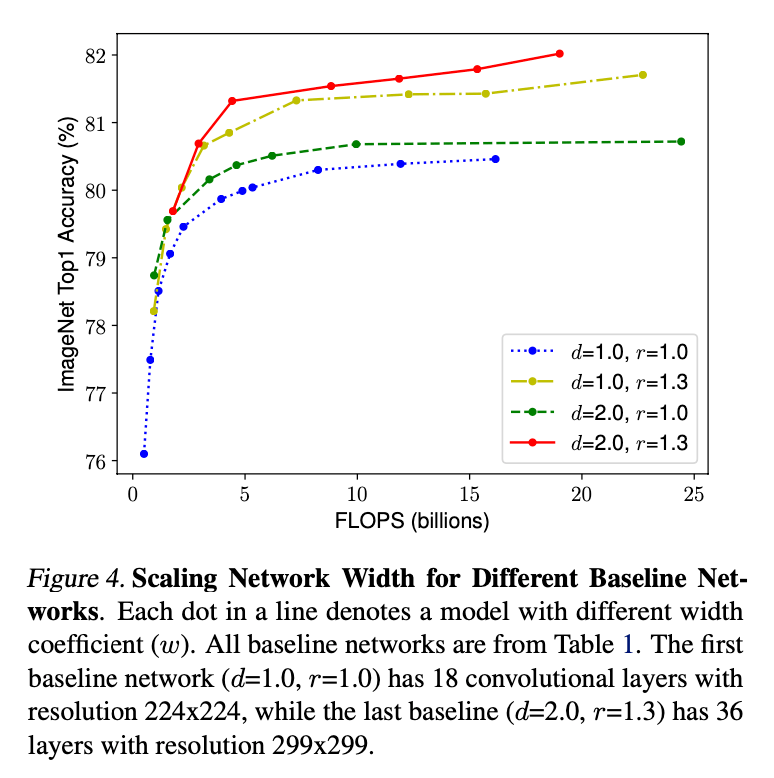
👉Observation 2
综上,我们的第二个发现是,为了追求更高的准确率和效率,在扩展卷积网络时,平衡网络的宽度、深度和分辨率是至关重要的。
事实上,一些先前的研究已经尝试通过任意方式平衡网络的宽度和深度,但这些方法都需要繁琐的手动调参。
我们提出了一种新的复合扩展方法,该方法使用一个复合系数$\phi$来统一扩展网络的宽度、深度和分辨率:
\[\begin{align} \text{depth:} \quad d &= \alpha^\phi \\ \text{width:} \quad w &= \beta^\phi \\ \text{resolution:} \quad r &= \gamma^\phi \\ \text{s.t.} \quad & \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \\ & \alpha \geq 1, \beta \geq 1, \gamma \geq 1 \end{align} \tag{3}\]其中,$\alpha,\beta,\gamma$是通过小范围网格搜索确定的常数。直观来说,$\phi$是一个由用户指定的系数。需要注意的是,常规卷积操作的FLOPS与$d,w^2,r^2$成正比,比如,将网络的深度加倍会使FLOPS加倍,而将网络的宽度或分辨率加倍则会使FLOPS增加四倍。由于卷积操作通常在卷积网络的计算成本中占主导地位,在使用公式(3)扩展卷积网络时,总的FLOPS会近似增加$(\alpha \cdot \beta^2 \cdot \gamma^2)^ \phi$。在本文中,我们限制$\alpha \cdot \beta^2 \cdot \gamma^2 \approx 2$,以确保对于任何新的$\phi$,总FLOPS将近似增加$2^{\phi}$。
4.EfficientNet Architecture
因为模型扩展不改变baseline网络中的层$\hat{\mathcal{F}}_i$,所以设计一个好的baseline网络也至关重要。我们在已有的卷积网络上评估了我们的扩展方法,但为了更好的证明我们扩展方法的有效性,我们提出了一个新的mobile-size的baseline网络,称为EfficientNet。
借鉴论文“Tan, M., Chen, B., Pang, R., Vasudevan, V., Sandler, M., Howard, A., and Le, Q. V. MnasNet: Platform-aware neural architecture search for mobile. CVPR, 2019.”,我们通过利用多目标神经框架搜索(multi-objective neural architecture search)开发了我们的baseline网络,该方法同时优化了准确率和FLOPS。具体来说,我们使用与论文“Tan, M., Chen, B., Pang, R., Vasudevan, V., Sandler, M., Howard, A., and Le, Q. V. MnasNet: Platform-aware neural architecture search for mobile. CVPR, 2019.”相同的搜索空间,并将$ACC(m) \times [FLOPS(m) / T]^w$作为优化目标,其中,$ACC(m)$和$FLOPS(m)$分别表示模型$m$的准确率和FLOPS,$T$是目标FLOPS,$w=-0.07$是控制准确率和FLOPS权衡的超参数。与论文“Tan, M., Chen, B., Pang, R., Vasudevan, V., Sandler, M., Howard, A., and Le, Q. V. MnasNet: Platform-aware neural architecture search for mobile. CVPR, 2019.”不同的是,我们优化的是FLOPS,而不是latency,因为我们并不针对任何特定的硬件设备。我们的搜索过程生成了一个高效的网络,我们将其命名为EfficientNet-B0。由于我们使用了与论文“Tan, M., Chen, B., Pang, R., Vasudevan, V., Sandler, M., Howard, A., and Le, Q. V. MnasNet: Platform-aware neural architecture search for mobile. CVPR, 2019.”相同的搜索空间,所以EfficientNet-B0的框架与MnasNet类似,但是由于我们的目标FLOPS更大(我们的目标FLOPS为400M),所以EfficientNet-B0会稍大一些。EfficientNet-B0的框架见表1。其主要结构为MBConv,并且我们还添加了squeeze-and-excitation optimization。
squeeze-and-excitation optimization论文:Hu, J., Shen, L., and Sun, G. Squeeze-and-excitation networks. CVPR, 2018.。
从baseline模型EfficientNet-B0开始,我们可以通过两步来应用我们提出的复合扩展方法:
- 第一步:首先固定$\phi = 1$,假定有超过两倍的可用资源,基于式(2)和式(3)对$\alpha,\beta,\gamma$进行小范围的网格搜索。对于EfficientNet-B0,我们实验得到的最优值为$\alpha=1.2,\beta=1.1,\gamma=1.15$,满足约束$\alpha \cdot \beta^2 \cdot \gamma^2 \approx 2$。
- 第二步:然后固定$\alpha,\beta,\gamma$,基于式(3),使用不同的$\phi$,就得到了EfficientNet-B1到B7,详见表2。

需要注意的是,直接在大型模型上搜索$\alpha,\beta,\gamma$参数,可以实现更好的性能,但在大型模型上进行搜索的成本会变得极其高昂。我们的方法解决了这个问题:仅在一个小型baseline网络上进行一次搜索(第一步),然后将相同的扩展系数应用于所有其他模型(第二步)。
5.Experiments
5.1.Scaling Up MobileNets and ResNets

5.2.ImageNet Results for EfficientNet
EfficientNet在ImageNet上的训练设置和论文“Tan, M., Chen, B., Pang, R., Vasudevan, V., Sandler, M., Howard, A., and Le, Q. V. MnasNet: Platform-aware neural architecture search for mobile. CVPR, 2019.”差不多:使用RMSProp优化器(decay=0.9,momentum=0.9),batch norm momentum=0.99,weight decay=1e-5,初始学习率为0.256且每2.4个epoch衰减为原来的0.97倍。我们还使用了SiLU激活函数、AutoAugment和stochastic depth(存活概率为0.8)。众所周知,更大的模型需要更多的正则化,我们将dropout比率从EfficientNet-B0的0.2线性增加到B7的0.5。我们从training数据集中随机选择25K张图像作为minival数据集,并且在minival上执行了early stopping,然后在validation数据集上进行了评估并汇报了准确率。结果详见表2。
AutoAugment论文:Cubuk, E. D., Zoph, B., Mane, D., Vasudevan, V., and Le, Q. V. Autoaugment: Learning augmentation policies from data. CVPR, 2019.。
stochastic depth论文:Huang, G., Sun, Y., Liu, Z., Sedra, D., and Weinberger, K. Q. Deep networks with stochastic depth. ECCV, pp. 646–661, 2016.。
Fig1是参数量和准确率的关系图,Fig5是FLOPS和准确率的关系图。

latency的测试结果见表4。

5.3.Transfer Learning Results for EfficientNet
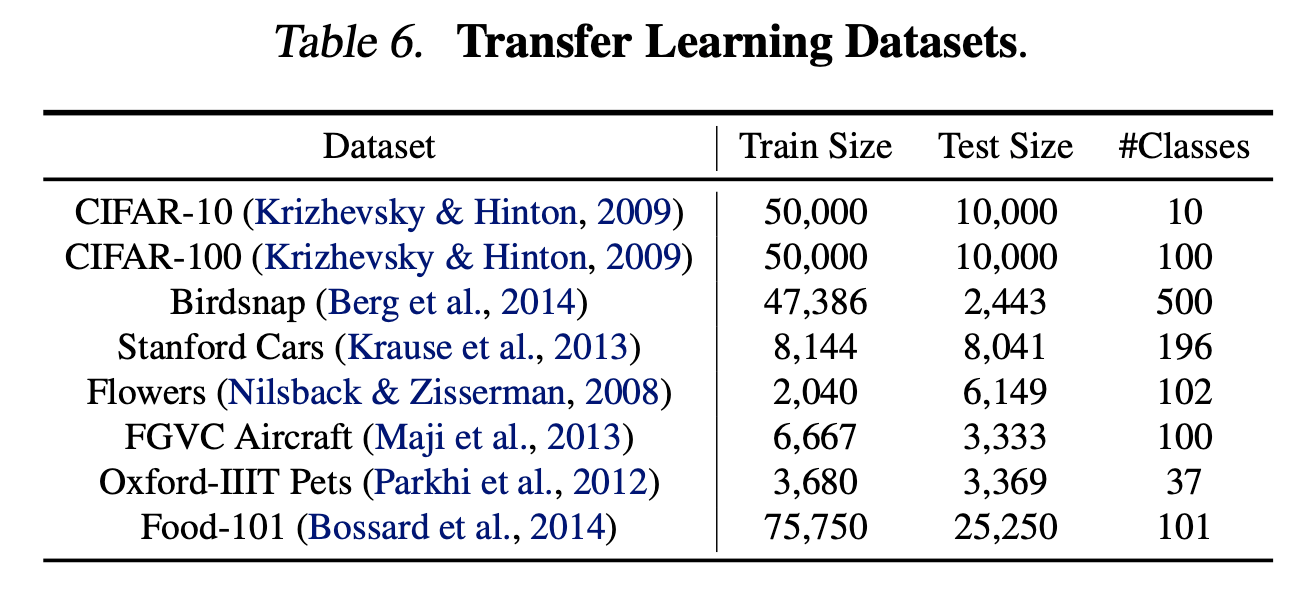
我们还在常见的一系列迁移学习数据集上评估了EfficientNet,这些数据集见表6。我们先在ImageNet上进行了预训练,然后在新数据集上进行了fine-tune。
测试结果见表5。

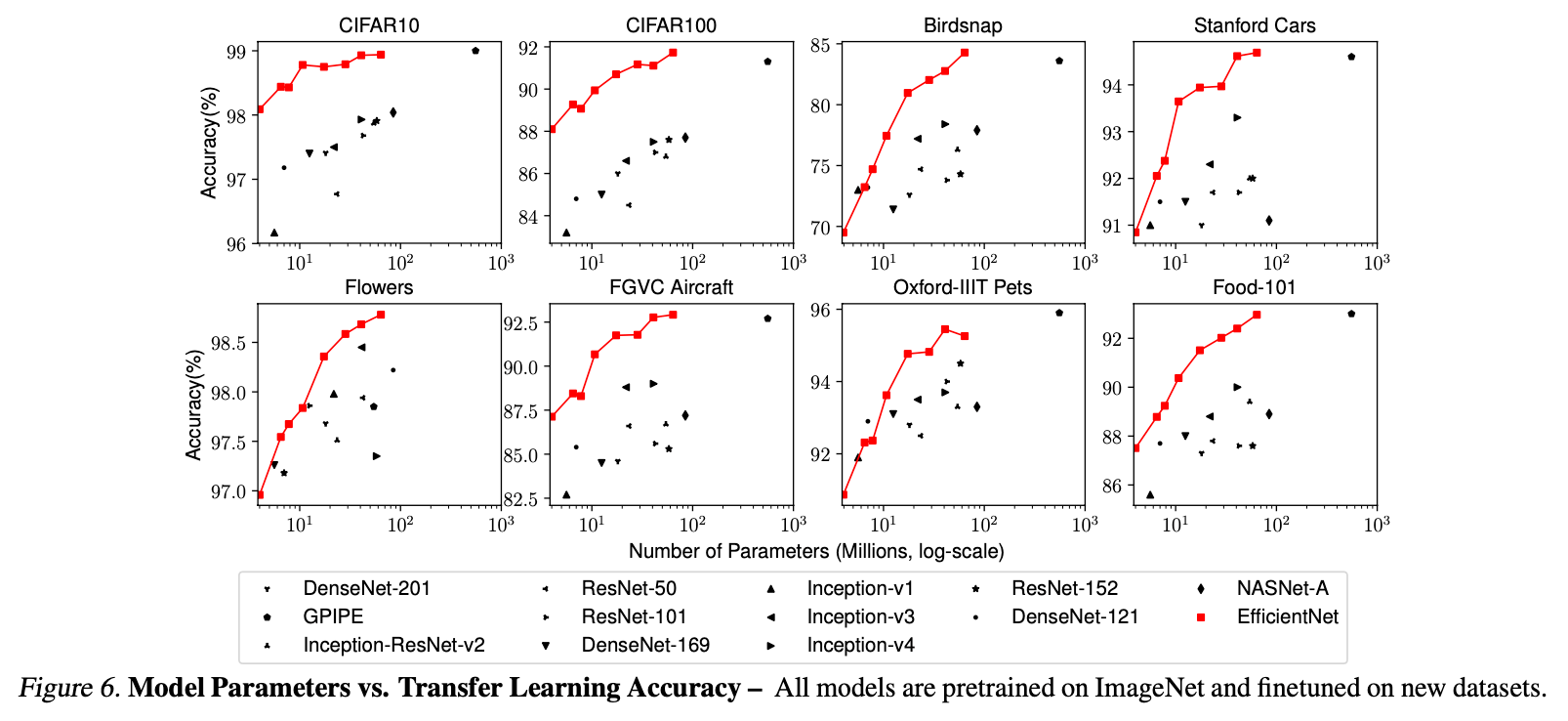
Fig6是参数量和准确率的关系图。
6.Discussion
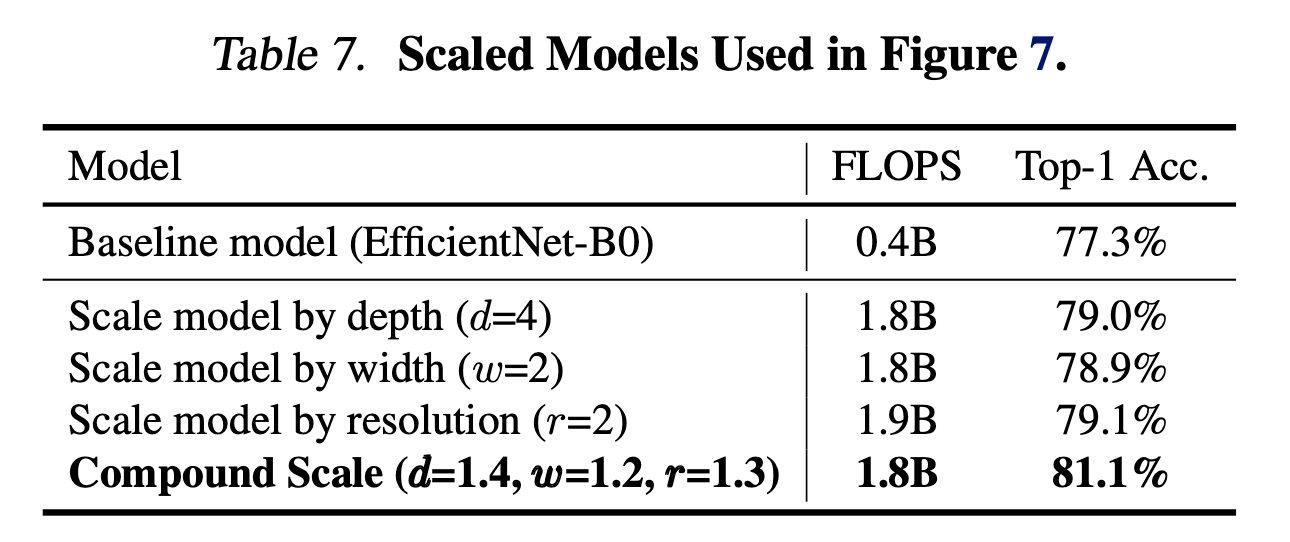
基于EfficientNet-B0,不同扩展方法的比较见Fig8。

为了进一步理解为什么我们提出的复合扩展方法优于其他扩展方法,Fig7比较了不同扩展模型的class activation map。
class activation map论文:Zhou, B., Khosla, A., Lapedriza, A., Oliva, A., and Torralba, A. Learning deep features for discriminative localization. CVPR, pp. 2921–2929, 2016.。

所有这些扩展模型都基于相同的baseline,它们的统计信息见表7。
7.Conclusion
不再赘述。
8.Appendix
9.原文链接
👽EfficientNet:Rethinking Model Scaling for Convolutional Neural Networks