【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.马尔可夫随机场
马尔可夫随机场(Markov Random Field,简称MRF)是典型的马尔可夫网,这是一种著名的无向图模型。图中每个结点表示一个或一组变量,结点之间的边表示两个变量之间的依赖关系。马尔可夫随机场有一组势函数(potential functions),亦称“因子”(factor),这是定义在变量子集上的非负实函数,主要用于定义概率分布函数。
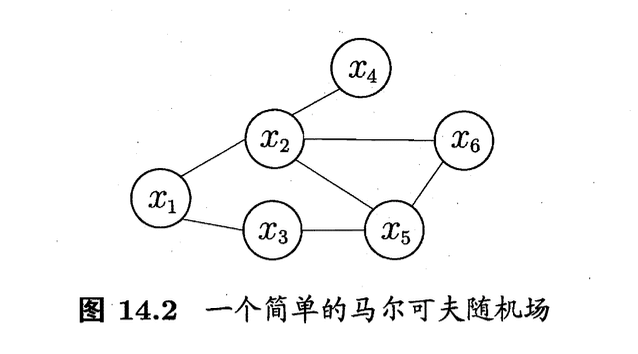
图14.2显示出一个简单的马尔可夫随机场。对于图中结点的一个子集,若其中任意两结点间都有边连接,则称该结点子集为一个“团”(clique)。若在一个团中加入另外任何一个结点都不再形成团,则称该团为“极大团”(maximal clique);换言之,极大团就是不能被其他团所包含的团。例如,在图14.2中,$\{x_1,x_2\},\{x_1,x_3\},\{x_2,x_4\},\{x_2,x_5\},\{x_2,x_6\},\{x_3,x_5\},\{x_5,x_6\}$和$\{x_2,x_5,x_6\}$都是团,并且除了$\{x_2,x_5 \},\{x_2,x_6 \}$和$\{x_5,x_6\}$之外都是极大团;但是,因为$x_2$和$x_3$之间缺乏连接,$\{x_1,x_2,x_3\}$并不构成团。显然,每个结点至少出现在一个极大团中。
在马尔可夫随机场中,多个变量之间的联合概率分布能基于团分解为多个因子的乘积,每个因子仅与一个团相关。具体来说,对于$n$个变量$\mathbf{x}=\{x_1,x_2,…,x_n\}$,所有团构成的集合为$\mathcal{C}$,与团$Q \in \mathcal{C}$对应的变量集合记为$\mathbf{x}_Q$,则联合概率$P(\mathbf{x})$定义为:
\[P(\mathbf{x}) = \frac{1}{Z} \prod_{Q\in \mathcal{C}} \psi _Q(\mathbf{x}_Q) \tag{1}\]其中$\psi_Q$为与团$Q$对应的势函数,用于对团$Q$中的变量关系进行建模,$Z=\sum_{\mathbf{x}}\prod _{Q\in \mathcal{C}}\psi_Q(\mathbf{x}_Q)$为规范化因子,以确保$P(\mathbf{x})$是被正确定义的概率。在实际应用中,精确计算$Z$通常很困难,但许多任务往往并不需获得$Z$的精确值。
显然,若变量个数较多,则团的数目将会很多(例如,所有相互连接的两个变量都会构成团),这就意味着式(1)会有很多乘积项,显然会给计算带来负担。注意到若团$Q$不是极大团,则它必被一个极大团$Q^*$所包含,即$\mathbf{x}_Q \subseteq \mathbf{x}_{Q^*}$;这意味着变量$\mathbf{x}_Q$之间的关系不仅体现在势函数$\psi_Q$中,还体现在$\psi_{Q^*}$中。于是,联合概率$P(\mathbf{x})$可基于极大团来定义。假定所有极大团构成的集合为$\mathcal{C}^*$,则有:
\[P(\mathbf{x})=\frac{1}{Z^*} \prod _{Q\in \mathcal{C}^*} \psi _Q (\mathbf{x}_Q) \tag{2}\]其中$Z^*=\sum_{\mathbf{x}}\prod _{Q \in \mathcal{C}^*}\psi _Q (\mathcal{x}_Q)$为规范化因子。例如图14.2中$\mathbf{x}=\{x_1,x_2,…,x_6 \}$,联合概率分布$P(\mathcal{x})$定义为:
\[P(\mathbf{x})=\frac{1}{Z}\psi_{12}(x_1,x_2)\psi_{13}(x_1,x_3)\psi_{24}(x_2,x_4)\psi_{35}(x_3,x_5)\psi_{256}(x_2,x_5,x_6)\]其中,势函数$\psi_{256}(x_2,x_5,x_6)$定义在极大团$\{ x_2,x_5,x_6 \}$上,由于它的存在,使我们不再需为团$\{x_2,x_5\}$,$\{x_2,x_6\}$和$\{x_5,x_6 \}$构建势函数。
在马尔可夫随机场中如何得到“条件独立性”呢?同样借助“分离”的概念,如图14.3所示,若从结点集$A$中的结点到$B$中的结点都必须经过结点集$C$中的结点,则称结点集$A$和$B$被结点集$C$分离,$C$称为“分离集”(separating set)。对马尔可夫随机场,有:
- “全局马尔可夫性”(global Markov property):给定两个变量子集的分离集,则这两个变量子集条件独立。
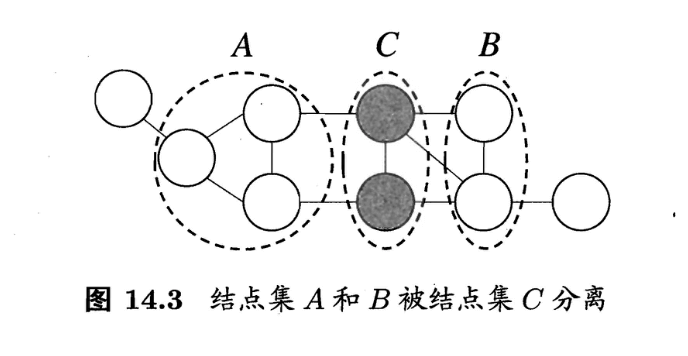
也就是说,图14.3中若令$A$,$B$和$C$对应的变量集分别为$\mathbf{x}_A$,$\mathbf{x}_B$和$\mathbf{x}_C$,则$\mathbf{x}_A$和$\mathbf{x}_B$在给定$\mathbf{x}_C$的条件下独立,记为$\mathbf{x}_A \perp \mathbf{x}_B \mid \mathbf{x}_C$。
下面我们做一个简单的验证。为便于讨论,我们令图14.3中的$A$,$B$和$C$分别对应单变量$x_A$,$x_B$和$x_C$,于是图14.3简化为图14.4。
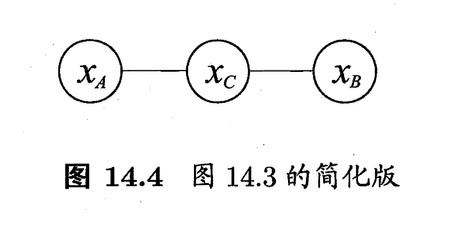
对于图14.4,由式(1)可得联合概率:
\[P(x_A,x_B,x_C)=\frac{1}{Z}\psi_{AC}(x_A,x_C)\psi_{BC}(x_B,x_C) \tag{3}\]基于条件概率的定义可得:
\[\begin{align*} P(x_A,x_B\mid x_C) &= \frac{P(x_A,x_B,x_C)}{P(x_C)} = \frac{P(x_A,x_B,x_C)}{\sum_{x'_A}\sum_{x' _B} P(x'_A,x'_B,x_C)} \\&= \frac{\frac{1}{Z}\psi_{AC}(x_A,x_C)\psi_{BC}(x_B,x_C)}{\sum_{x'_A}\sum_{x'_B}\frac{1}{Z}\psi_{AC}(x'_A,x_C)\psi_{BC}(x'_B,x_C)} \\&= \frac{\psi_{AC}(x_A,x_C)}{\sum_{x'_A}\psi_{AC}(x'_A,x_C)} \cdot \frac{\psi_{BC}(x_B,x_C)}{\sum_{x'_B}\psi_{BC}(x'_B,x_C)} \end{align*} \tag{4}\] \[\begin{align*} P(x_A \mid x_C) &= \frac{P(x_A,x_C)}{P(x_C)} = \frac{\sum_{x'_B}P(x_A,x'_B,x_C)}{\sum_{x'_A}\sum_{x'_B}P(x'_A,x'_B,x_C)} \\&= \frac{\sum_{x'_B}\frac{1}{Z}\psi_{AC}(x_A,x_C)\psi_{BC}(x'_B,x_C)}{\sum_{x'_A}\sum_{x'_B}\frac{1}{Z}\psi_{AC}(x'_A,x_C)\psi_{BC}(x'_B,x_C)} \\&= \frac{\psi_{AC}(x_A,x_C)}{\sum_{x'_A}\psi_{AC}(x'_A,x_C)} \end{align*} \tag{5}\]由式(4)和(5)可知:
\[P(x_A,x_B \mid x_C) = P(x_A \mid x_C)P(x_B \mid x_C) \tag{6}\]即$x_A$和$x_B$在给定$x_C$时条件独立。
由全局马尔可夫性可得到两个很有用的推论:
- 局部马尔可夫性(local Markov property):给定某变量的邻接变量(个人注解:指的是所有邻接变量的集合),则该变量条件独立于其他变量。形式化地说,令$V$为图的结点集,$n(v)$为结点$v$在图上的邻接结点集合,$n^*(v)=n(v) \cup \{v\}$,有$\mathbf{x}_v \perp \mathbf{x}_{V \setminus n^*(v)} \mid \mathbf{x}_{n(v)}$。
- 成对马尔可夫性(pairwise Markov property):给定所有其他变量,两个非邻接变量条件独立。形式化地说,令图的结点集和边集分别为$V$和$E$,对图中的两个结点$u$和$v$,若$\langle u,v \rangle \notin E$,则$\mathbf{x}_u \perp \mathbf{x}_v \mid \mathbf{x}_{V \setminus \langle u,v \rangle}$。
某变量的所有邻接变量组成的集合称为该变量的“马尔可夫毯”(Markov blanket)。
现在我们来考察马尔可夫随机场中的势函数。显然,势函数$\psi_Q(\mathbf{x}_Q)$的作用是定量刻画变量集$\mathbf{x}_Q$中变量之间的相关关系,它应该是非负函数,且在所偏好的变量取值上有较大函数值。例如,假定图14.4中的变量均为二值变量,若势函数为:
\[\psi_{AC}(x_A,x_C) = \begin{cases} 1.5, & \text{if} \ x_A=x_C; \\ 0.1, & \text{otherwise,} \end{cases}\] \[\psi_{BC}(x_B,x_C) = \begin{cases} 0.2, & \text{if} \ x_B=x_C; \\ 1.3, & \text{otherwise,} \end{cases}\]则说明该模型偏好变量$x_A$与$x_C$拥有相同的取值,$x_B$与$x_C$拥有不同的取值;换言之,在该模型中$x_A$与$x_C$正相关,$x_B$与$x_C$负相关。结合式(1)易知,令$x_A$与$x_C$相同且$x_B$与$x_C$不同的变量值指派将取得较高的联合概率。
为了满足非负性,指数函数常被用于定义势函数,即:
\[\psi_Q(\mathbf{x}_Q)=e^{-H_Q(\mathbf{x}_Q)} \tag{7}\]$H_Q(\mathbf{x}_Q)$是一个定义在变量$\mathbf{x}_Q$上的实值函数,常见形式为:
\[H_Q(\mathbf{x}_Q)= \sum_{u,v\in Q,u\neq v} \alpha_{uv}x_ux_v+\sum_{v\in Q}\beta_v x_v \tag{8}\]其中$\alpha_{uv}$和$\beta_v$是参数。上式中的第二项仅考虑单结点,第一项则考虑每一对结点的关系。
2.关于式(1)的理解
假设$n$个变量$\mathbf{x}=\{x_1,x_2,…,x_n\}$都是二值型,即不是0就是1,那么$P$可以是$P(x_1=0,x_2=0,…,x_n=0)$,或者$P(x_1=0,x_2=0,…,x_n=1)$,一共有$2^n$种取值组合,而$Z$就是为了确保这些组合的概率加起来总和为1,即$\sum_{\mathbf{x}}P(\mathbf{x})=1$。