本文为原创文章，未经本人允许，禁止转载。转载请注明出处。
1.最大流问题
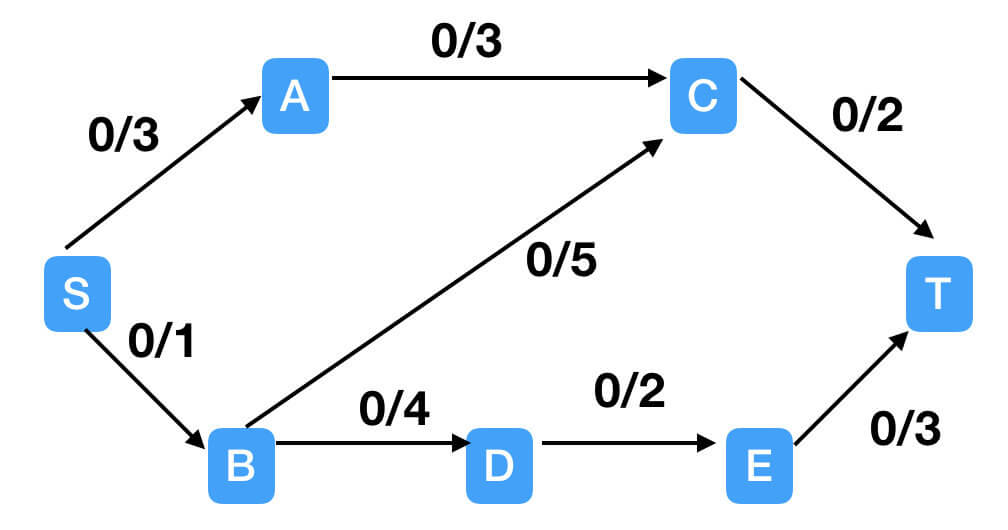如上图所示，如果起点为S点，终点为T点，有水流从S点流向到T点。图中黑色带箭头的直线为管道，水流只能按照箭头的方向前进，很明显，一个管道中不可能有两种方向的水流。“/”前的数字表示该条管道目前的流量，“/”后面的数字表示该条管道能承载的最大流量。水流从S点出发，集结到T点，S点出发的流和进入T点的流应该是相等的。最大流问题就是使流尽可能的大（在满足每条边容量的限制下）。
解决最大流问题通常有两种方法：
- 增广路径算法（augmenting paths）
- 预流推进算法（push-relabel）
本文主要介绍增广路径算法以及Graph Cut图割算法中所用的最大流-最小割算法。
2.增广路径算法
增广路径算法主要有：Fold-Fulkerson算法，Edmonds-Karp算法，Dinic算法等。其中，Fold-Fulkerson 是最基本的增广路径思想，也是本博客要主要介绍的一种算法。
2.1.基本术语
通常将第1部分中的那张图称之为容量网络，对于容量网络中的一条边$(u,v)$，该边的上限称为容量，记作$c(u,v)$。实际流量记作$f(u,v)$。
$c(u,v)-f(u,v)$为剩余的容量，也称为残量。任意时刻，图中残量不为0的边组成的网络被称为残余网络，该网络上从s到t的路径被称为增广路径。
2.2.增广路径算法的主体思想
不断地从S点开始寻找增广路径，每次都对其进行增广，直到S点和T点不连通（因为残余网络的边的残量如果为0则从残余网络中删去这条边，所以最后会造成S点和T点不连通），也就是找不到增广路径为止（因为如果S点和T点连通，就意味着还存在增广路径）。当找不到增广路径的时候，当前的流量就是最大流。
接下来我们演示一下增广路径算法是怎么实现的：
STEP1：将容量网络转化成残余网络。
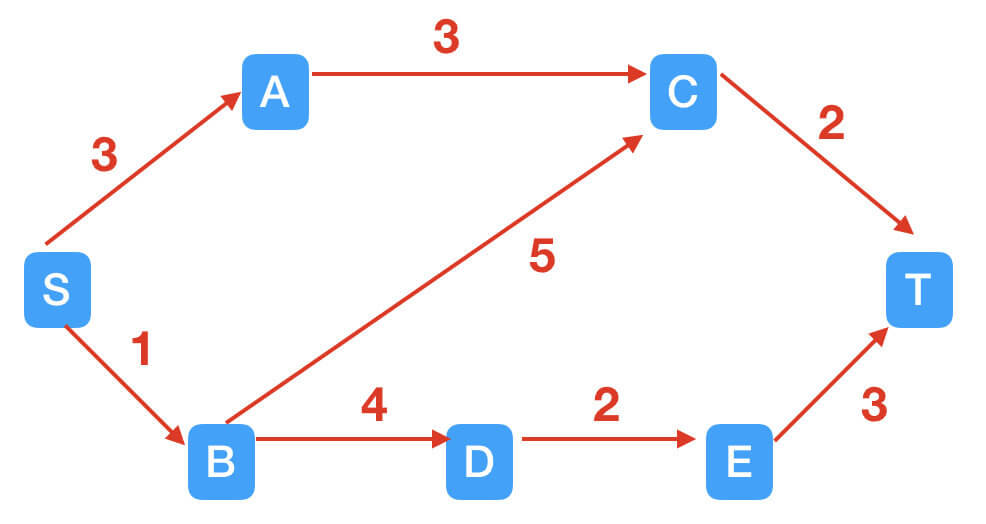
STEP2：找到增广路径S$\rightarrow$A$\rightarrow$C$\rightarrow$T。
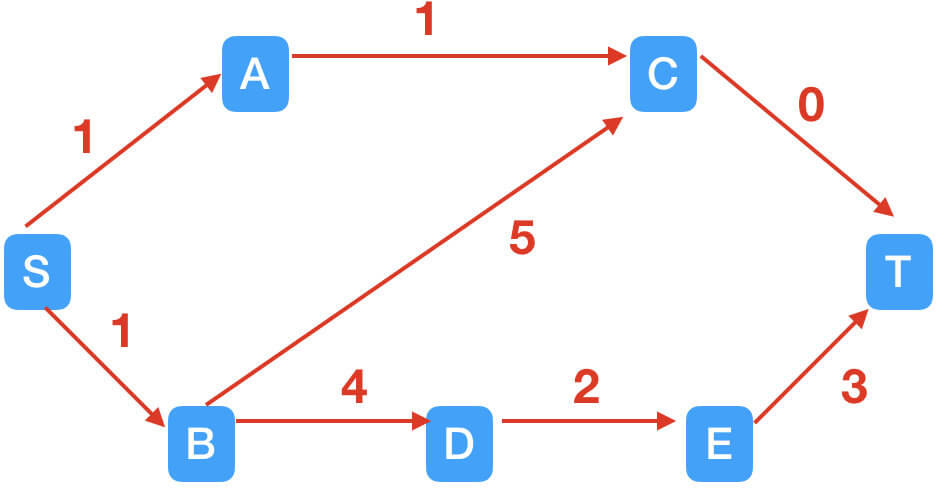
STEP3：找到增广路径S$\rightarrow$B$\rightarrow$D$\rightarrow$E$\rightarrow$T。
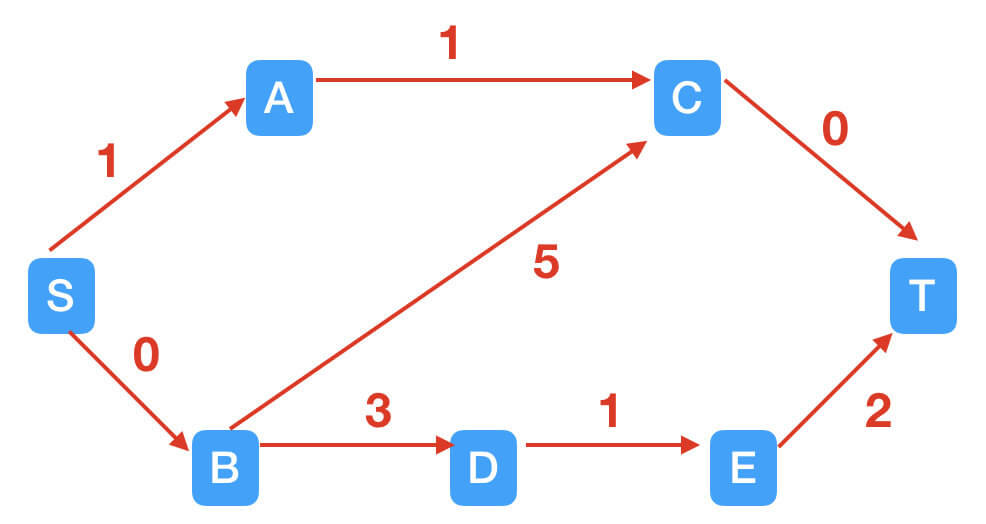
至此，找不到其他增广路径了，最大流为3，最大流问题解决。
但是这里存在一个问题，如果我们在STEP2找到的是路径S$\rightarrow$B$\rightarrow$C$\rightarrow$T，残余网络见下图：
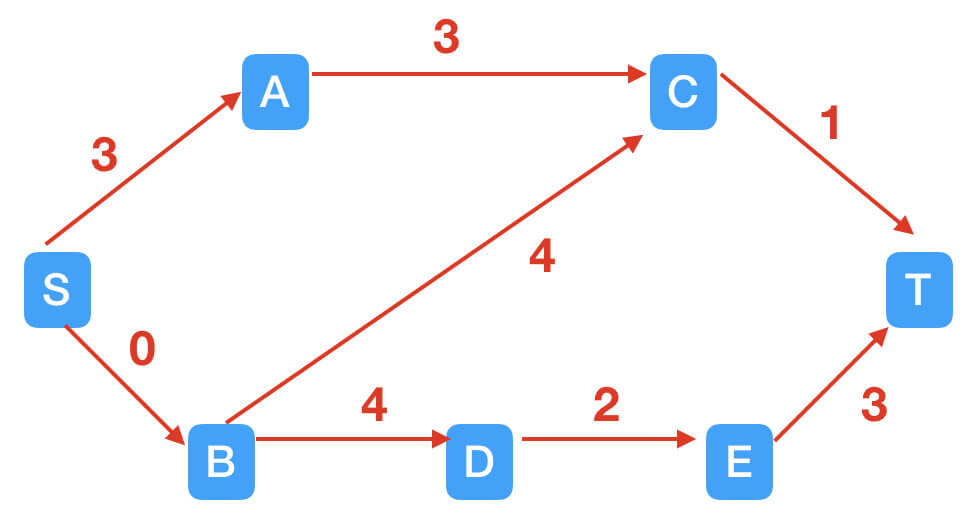然后下一步找到路径S$\rightarrow$A$\rightarrow$C$\rightarrow$T：
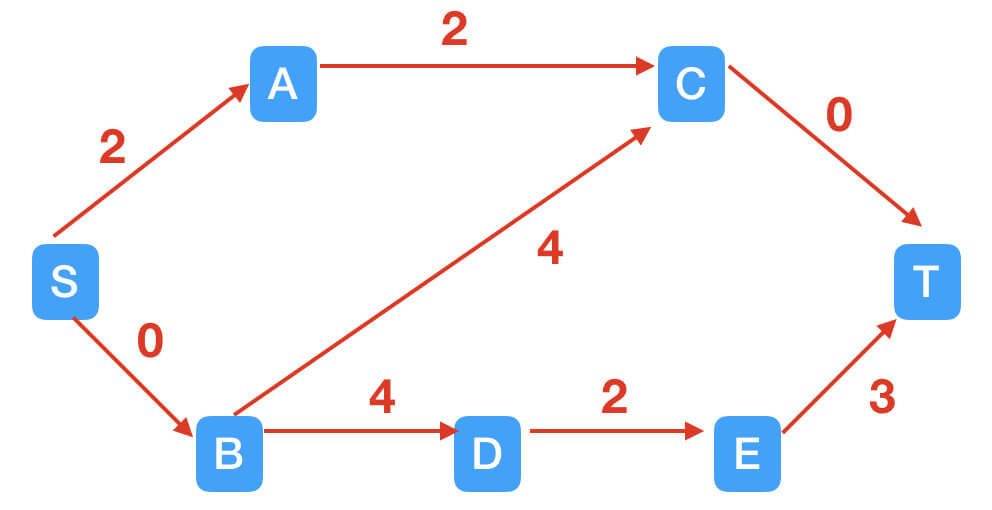此时，也满足残余网络S点和T点不连通，找不到其他增广路径等条件，但是最大流为2，这个结果明显不是最大流。这里，引入Fold-Fulkerson算法来解决这个问题。
2.3.Fold-Fulkerson算法
Fold-Fulkerson算法的核心思想就是引入反向边，正向边流了k个单位的流量，其反向边的残量增加k。
STEP1：引入反向边。
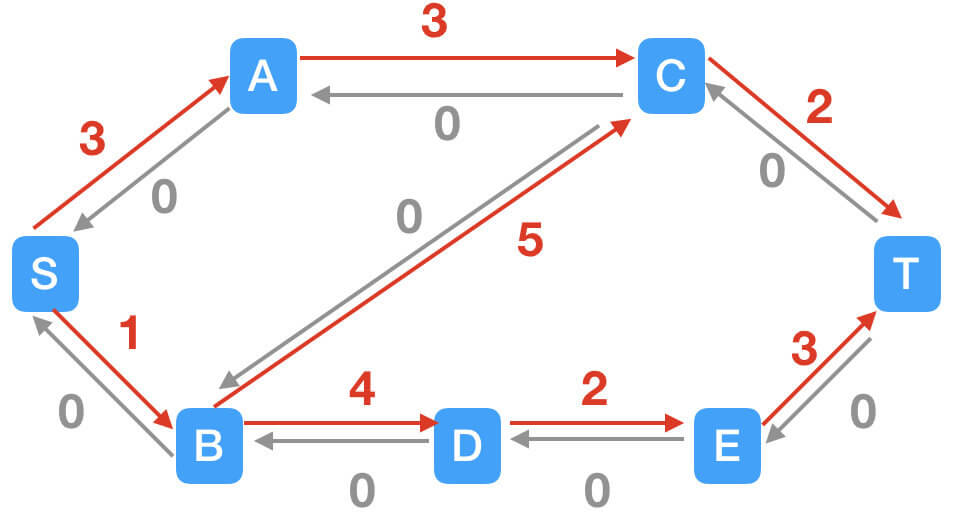
STEP2：找到路径S$\rightarrow$B$\rightarrow$C$\rightarrow$T。
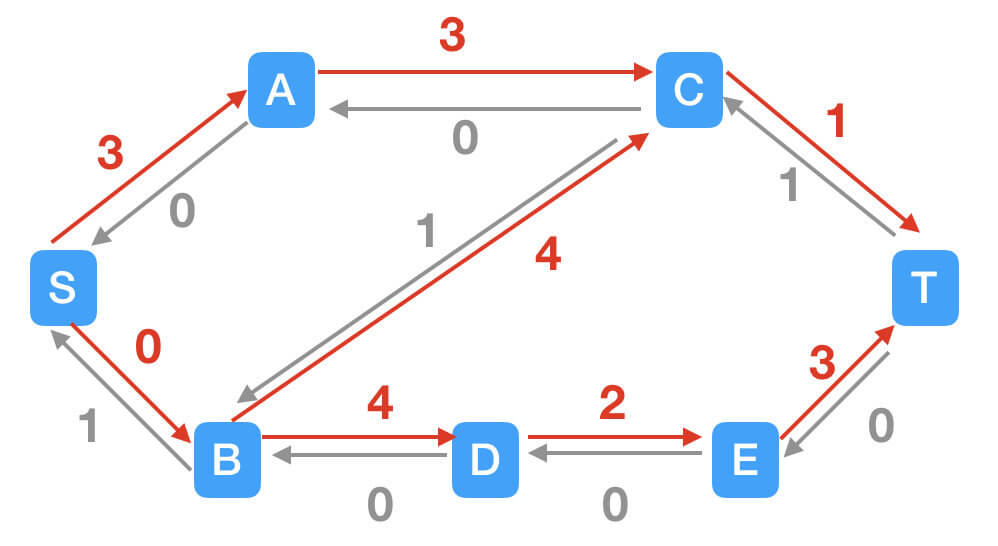
STEP3：找到路径S$\rightarrow$A$\rightarrow$C$\rightarrow$T。
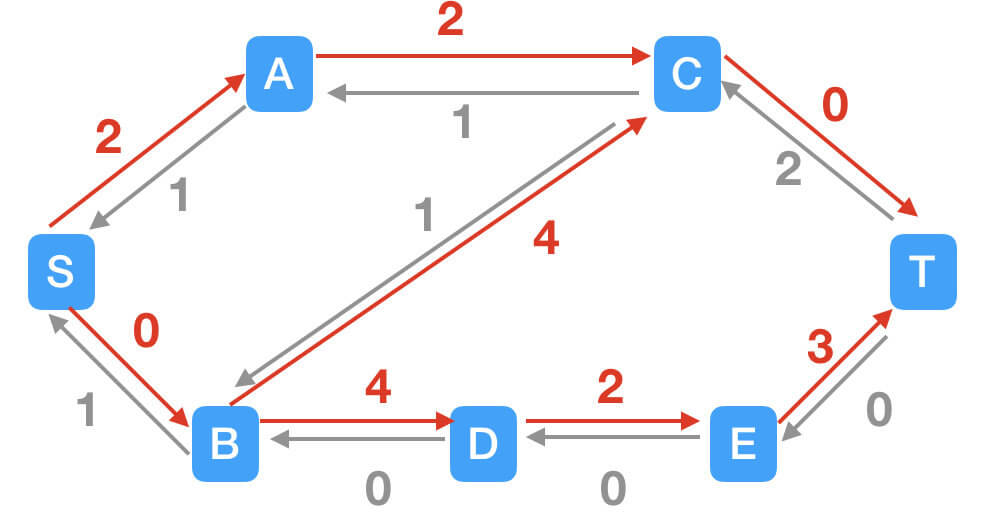
STEP4：正向边此时已经不存在增广路径，但是在引入反向边之后，出现了一条新的增广路径：S$\rightarrow$A$\rightarrow$C$\rightarrow$B$\rightarrow$D$\rightarrow$E$\rightarrow$T。
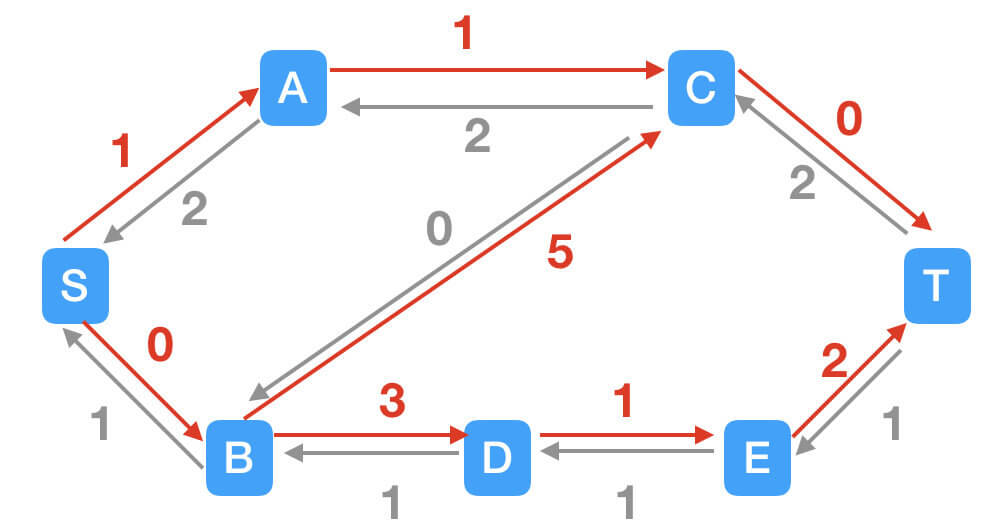
此时，彻底不存在增广路径，最大流为3，得到的结果与2.2部分正确结果一样。
2.4.搜索路径的方法
主要有两种搜索方法：宽度优先搜索（BFS）和深度优先搜索（DFS）。
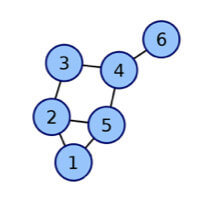
- BFS（宽度优先搜索，广度优先搜索）：如果从1开始进行搜索的话，BFS的步骤就是，先搜索所有和1相连的，也就是2和5被找到了，然后再从2开始搜索和他相连的，也就是3被找到了，然后从5搜，也就是4被找到了，然后从3开始搜索，4被找到了，但是4之前已经被5找到了，所以忽略掉就行。然后3开始搜索，忽略4所以啥都没搜到，然后从4开始，6被找到了。
- DFS（深度优先搜索）：DFS的话从1开始，先找到其中一个相连的，2被找到了，然后直接开始从2开始搜索，3被找到了，然后从3开始搜索，4被找到了，然后从4开始搜索，5被找到了，然后从5开始搜索，忽略已经找到的所以啥都没找到。然后没路可走了，回到前面去再走另一条路，从4开始，6被找到了，然后又没路可走了，然后再回去前面4，然后没路了 ，回去前面3，然后一直这样。
3.最大流和最小割的关系
最大流最小割定理是指在一个网络流中，能够从源点（S点）到达汇点（T点）的最大流量等于如果从网络中移除就能够导致网络流中断的边的集合的最小容量和。即在任何网络中，最大流的值等于最小割的容量。
一个重要的相关定理：如果f是网络中的一个流，CUT(S,T)是任意一个割，那么f的值等于正向割边的流量与负向割边的流量之差。换种说法就是，任意一个流小于等于任意一个割。
最大流等于最小割的证明：
设相等的流和割分别为$F_m$和$C_m$。则因为任意一个流小于等于任意一个割。$任意F≤F_m=C_m≤任意C$。证明完成。
我们根据之前的例子来验证一下：
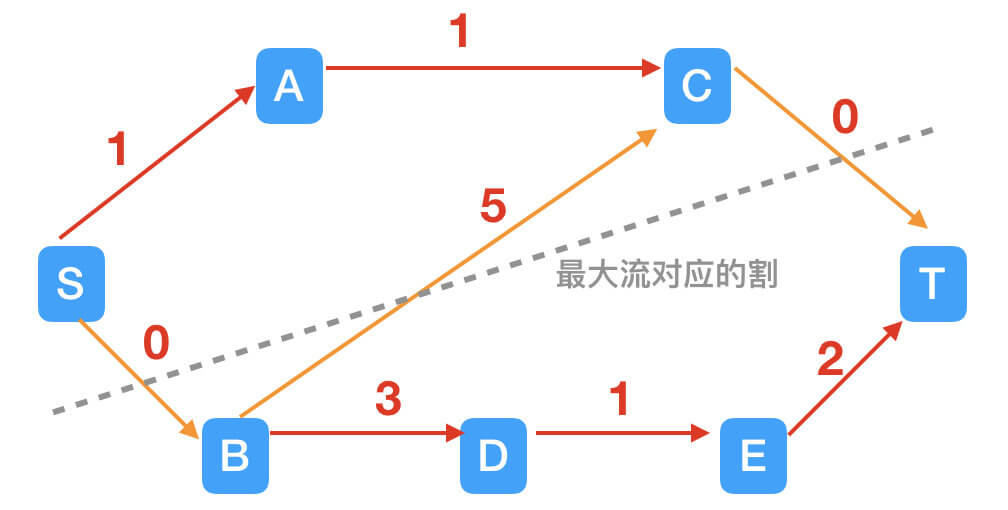割的净流：$f=f(C,T)-f(B,C)+f(S,B)=2-0+1=3=max-flow$
4.Graph Cut中所用的最大流/最小割算法
先附上论文地址和OpenCV中的源码地址：
论文链接👉An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision.
OpenCV源码地址👉maxflow
Graph Cut中所用的最大流/最小割算法是在Fold-Fulkerson算法基础上的改进，使用BFS方法寻找路径。接下来让我们一探究竟吧。
关于Graph Cut算法的详细介绍请见本人的另一篇博客：【图像分割】Graph Cut算法
4.1.背景知识
首先，构建有向加权图$G=<V,E>$，V是节点，E是有向边，如下图所示：
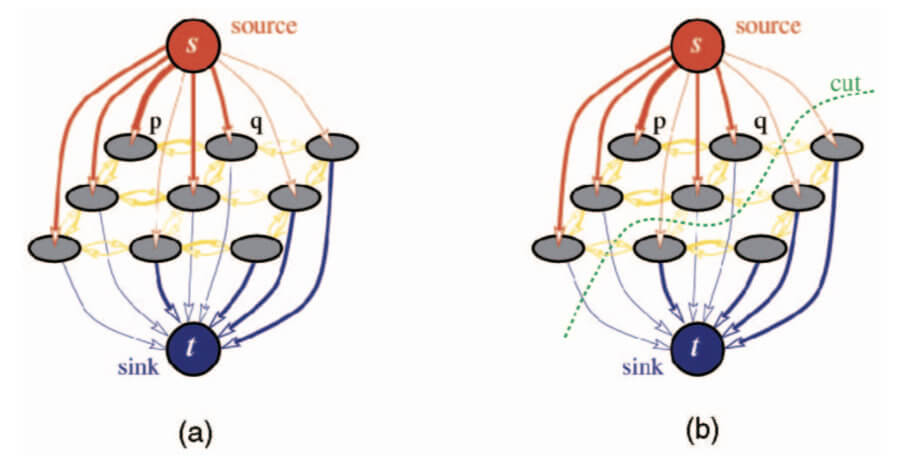通常情况下，节点可以是像素，体素或者其他特征。s和t是被称为终端的附加特殊节点。图中所有的边都分配有权重或者代价。$(p,q)$的代价可能和$(q,p)$的代价不一样，这一点在图像分析的很多应用场景中是很重要的。
图(b)中，割C将图分为两个互斥的子集S和T，源点s属于S，汇点t属于T。 找到所有割中代价最小的割（即最小割）可以通过最大流（从源点s到汇点t）解决。
4.2.新的最小割/最大流算法
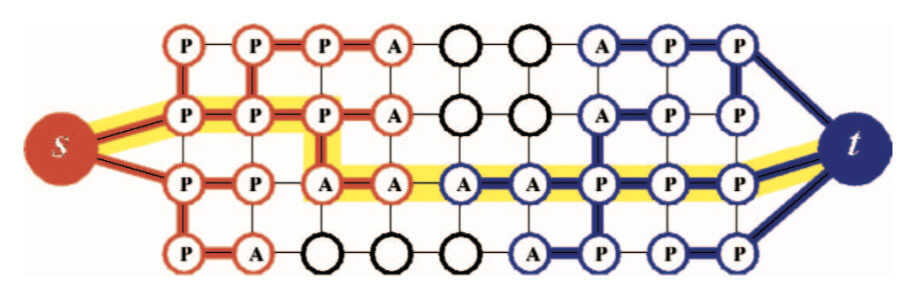如上图所示，构建了两个不重叠的搜索树S和T，有$S\in V,s\in S,T\in V,t\in T,S\cap T=\emptyset$。两棵树的根节点分别是s和t。在树S中，从每个父节点到其子节点的所有边都是不饱和的，而在树T中，从子节点到其父节点的边是不饱和的。（树S中的所有边都是由父节点指向子节点（存在流量），树T中则由子节点指向父节点）。
树S和树T中的节点分为“主动”(A)和“被动”(P)两种。主动节点允许树继续生长，代表每个树的边界。被动节点不能生长，因为它们完全被来自同一树的其他节点阻塞。既不属于S也不属于T的节点称为自由节点。
该算法迭代重复以下三个阶段：
- “生长”阶段：搜索树S和T扩展节点，直到两树相遇，得到一条由源点s到汇点t的增广路径。
- “增广”阶段：根据找到的增广路径将搜索树拆分为子树或森林。
- “领养”阶段：搜索树S和T重新构建。
在开始详细讲解三个阶段之前，再来了解一些会用到的符号的含义：
用tree_cap$(p\rightarrow q)$表示剩余容量。$TREE(p)=S$或$TREE(p)=T$表示$p$属于树S或树T。
4.2.1.“生长”阶段(Growth Stage)
while循环执行的条件：$A\neq \emptyset$，即主动节点的集合A不能为空集。
while循环第一步：选择主动节点$p\in A$。
while循环第二步：$q$对$p$的邻居节点，判断tree_cap$(p\rightarrow q)$是否大于0，即是否是饱和边。如果大于0，执行for循环，否则，执行while循环第三步。
for循环第一步：如果$TREE(q)=\emptyset$，则将$q$设为对应搜索树的主动节点，有$TREE(q)=TREE(p),PARENT(q)=p$，将$q$节点加到集合A中，$A=A\cup \lbrace q \rbrace$（符号“:=”的意思是“定义为”）。
for循环第二步：如果$TREE(q)\neq \emptyset$，且$TREE(q)\neq TREE(p)$，说明找到了增广路径，返回$P=PATH_{s\rightarrow t}$。
while循环第三步：将$p$从集合A中移除（经历过for循环之后，节点$p$从主动节点变为被动节点）。
如果一直到while循环结束，都没有找到增广路径，则返回$P=\emptyset$。
4.2.2.“增广”阶段(Augmentation Stage)
“增广”阶段的输入就是“生长”阶段产生的增广路径$P$。
第一步：确定路径$P$中所有边的最小残余容量$\Delta$。
第二步：增广操作。路径$P$流入大小刚好为$\Delta$的流。
for循环判断语句：如果$P$中有边(p,q)变为饱和边，则执行for循环，否则，跳出for循环。
for循环第一步：如果$TREE(q)=TREE(p)=S$，则q没有父节点，即$PARENT(q)=\emptyset$，将q加入到孤儿节点的集合$O$中，即$O=O\cup \lbrace q \rbrace$。
for循环第二步：如果$TREE(q)=TREE(p)=T$，则p没有父节点，即$PARENT(p)=\emptyset$，将p加入到孤儿节点的集合$O$中，即$O=O\cup \lbrace p \rbrace$。
结束for循环。
4.2.3.“领养”阶段(Adoption Stage)
这一阶段主要处理集合$O$中的所有孤儿节点。
每个孤儿节点$p$在同一树内都尝试去寻找一个新的有效的父节点。如果成功，$p$保留在树中，并具有新的父节点；否则，它变成一个自由节点，它的所有子节点都变为孤儿节点加入到集合$O$中。
处理集合$O$中的每一个孤儿节点，直至$O=\emptyset$。
那么要怎么处理孤儿节点呢？
首先，在孤儿节点$p$的邻居节点中尝试找一个新的有效父节点。
有效的父节点$q$应该满足以下条件：
- 属于同一颗树$TREE(q)=TREE(p)$。
- $(q,p)$为不饱和边，即tree_cap$(q\rightarrow p)>0$。
- $q$的“起源“应该是源点s或者汇点t(注意：“起源”不能是其他自由节点或者孤儿节点)。
如果节点$p$找到了新的有效父节点$q$，则$PARENT(p)=q$。在这种情况下，$p$被保留在搜索树中，$p$的主动（或被动）状态保持不变。
另一种情况，如果$p$没有找到有效的父节点，则$p$变为自由节点，接下来的操作是：
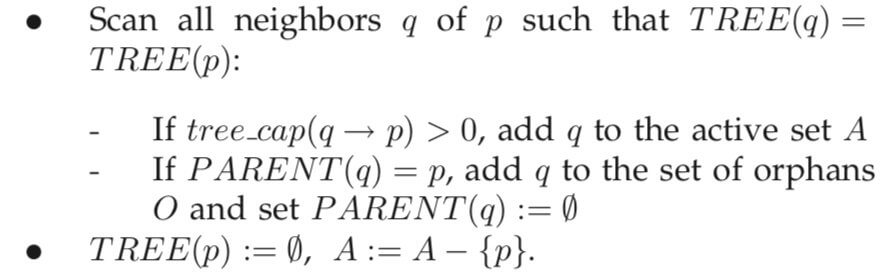1.扫描同一棵树内$p$的所有邻居节点$q$：
- 如果tree_cap$(q \rightarrow p)>0$，把$q$ 加到集合A中。
- 如果$PARENT(q)=p$，把$q$加到集合$O$中，同时设置$PARENT(q)=\emptyset$。即自由节点$p$的所有子节点全部变为孤儿节点。
2.$TREE（p）=\emptyset,A=A-\lbrace p \rbrace$。
