本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.泰勒公式
针对一元函数来说(也有针对多元函数的泰勒展开,此处仅讨论针对一元函数的展开):
如果函数足够光滑的话,在已知函数在某一点(假设为$x_0$)的各阶导数值的情况下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值:
\[f(x)=\frac{f(x_0)}{0!}+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+...+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x)\]其中,
- $f(x_0)$为0阶导数,即函数本身代入$x_0$。
- $0!=1$。
- $R_n(x)$为余项,即$(x-x_0)^n$的高阶无穷小:$o[(x-x_0)^n]$。
当$x_0=0$时:
\[f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+...+\frac{f^{(n)}(0)}{n!}x^n+R_n(x)\]此时,也称为麦克劳伦公式。
1.1.泰勒公式的余项
对于泰勒公式中余项的理解(以展开到一阶导数为例):
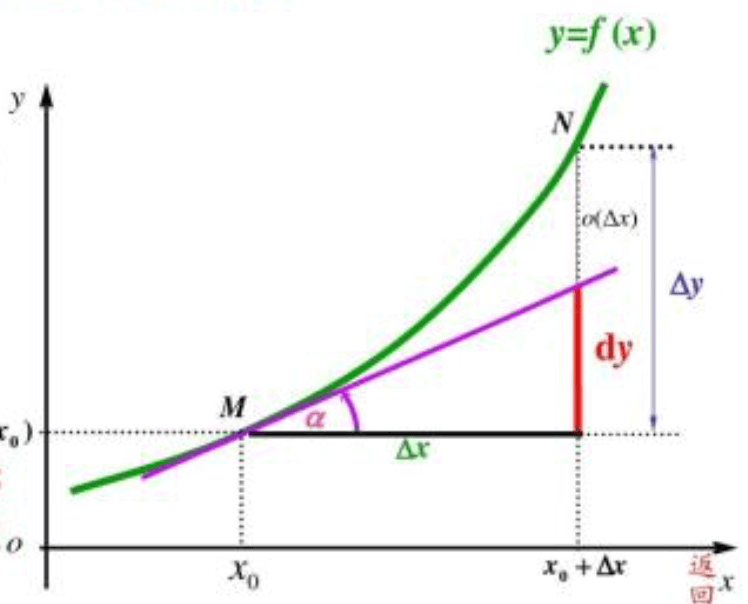
从图中可以很容易看出:
\[f(x)=f(x_0)+f'(x_0)\Delta x+o(\Delta x)\]所以用$f(x_0)+f’(x_0)\Delta x$这个多项式去近似$x_0$附近的函数值,但是存在一定误差。
泰勒公式的余项$R_n(x)$可以写成多种不同的形式:

1.2.泰勒公式的应用
1.2.1.例题1
$f(x)=e^x$的麦克劳伦公式(即$x_0=0$)。
解:
$f’(x)=f^{(2)}(x)=…=f^{(n)}(x)=e^x$
$f’(x_0)=f^{(2)}(x_0)=…=f^{(n)}(x_0)=e^0=1$
$x-x_0=x-0=x$
$f(x_0)=e^{x_0}=e^0=1$
所以$e^x$在0附近的泰勒展开为:
$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+…+\frac{x^n}{n!}+R_n(x)$
1.2.2.例题2
求$lim_{x\to 0}\frac{\sqrt{3x+4}+\sqrt{4-3x}-4}{x^2}$
📌方法一:$x\to 0$时,分子分母都为0且可导,可用洛必达法则。
📌方法二:使用泰勒公式。
在0附近,对$\sqrt{3x+4}$进行泰勒展开:
$x-x_0=x-0=x$
$f(x_0)=4^{\frac{1}{2}}=2$
$f’(x)=\frac{1}{2}(3x+4)^{-\frac{1}{2}}\times 3=\frac{3}{2}(3x+4)^{-\frac{1}{2}}$,所以:$f’(x_0)=f’(0)=\frac{3}{4}$
$f^{(2)}(x)=-\frac{3}{4}(3x+4)^{-\frac{3}{2}}\times 3=-\frac{9}{4}(3x+4)^{-\frac{3}{2}}$,所以:$f^{(2)}(x_0)=f^{(2)}(0)=-\frac{9}{32}$
因此在0附近,对$\sqrt{3x+4}$进行泰勒展开:$\sqrt{3x+4}=2+\frac{3}{4}x-\frac{9}{64}x^2+o(x^2)$
同理,$\sqrt{4-3x}=2-\frac{3}{4}x-\frac{9}{64}x^2+o(x^2)$
所以原式$=\lim_{x\to 0}\frac{2+\frac{3}{4}x-\frac{9}{64}x^2+2-\frac{3}{4}x-\frac{9}{64}x^2+o(x^2)-4}{x^2}=\lim_{x\to 0} \frac{-\frac{9}{32}x^2+o(x^2)}{x^2}=-\frac{9}{32}$
1.2.3.例题3
用泰勒展开证明洛必达法则:
首先有:$\lim_{x\to x_0}f(x)=0;\lim_{x\to x_0}g(x)=0$
\[\begin{align} \lim_{x\to x_0} \frac{f(x)}{g(x)} & = \lim_{x\to x_0} \frac{f(x_0)+f'(x_0)\Delta x+o(\Delta x)}{g(x_0)+g'(x_0)\Delta x+o(\Delta x)} \tag{1} \\ & = \lim_{\Delta x\to 0} \frac{f'(x_0)\Delta x+o(\Delta x)}{g'(x_0)\Delta x+o(\Delta x)} \\&= \lim_{\Delta x\to 0} \frac{f'(x_0)+o(\Delta x)/\Delta x}{g'(x_0)+o(\Delta x)/\Delta x} \tag{2} \\&= \frac{f'(x_0)}{g'(x_0)} \end{align}\]式(1)中分别对$f(x)$和$g(x)$进行泰勒展开。
式(2)中根据高阶无穷小,可得$\lim_{\Delta x\to0}\frac{o(\Delta x)}{\Delta x}=0$
1.3.二元函数的泰勒展开
二元函数在点$(x_k,y_k)$处的泰勒展开:
\[\begin{align} f(x,y) & = f(x_k,y_k) \\ & + (x-x_k)f'_x(x_k,y_k)+(y-y_k)f'_y(x_k,y_k) \\ & + \frac{1}{2!}(x-x_k)^2f^{(2)}_{xx}(x_k,y_k)+\frac{1}{2!}(x-x_k)(y-y_k)f^{(2)}_{xy}(x_k,y_k)+\frac{1}{2!}(x-x_k)(y-y_k)f^{(2)}_{yx}(x_k,y_k)+\frac{1}{2!}(y-y_k)^2f^{(2)}_{yy}(x_k,y_k) \\ & + 余项 \end{align}\]2.梯度
梯度定义:设二元函数$z=f(x,y)$在平面区域$D$上具有一阶连续偏导数,则对于每一个点$P(x,y)$都可定出一个向量:$\lbrace \frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\rbrace=f_x(x,y)\vec i+f_y(x,y)\vec j$,该函数就称为函数$z=f(x,y)$在点$P(x,y)$的梯度,记作$grad f(x,y)$或$\nabla f(x,y)$,即有:
\[grad f(x,y)=\nabla f(x,y)=\{\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\}=f_x(x,y)\vec i+f_y(x,y)\vec j\]其中$\nabla=\frac{\partial}{\partial x}\vec i+\frac{\partial}{\partial y}\vec j$称为(二维的)向量微分算子或Nabla算子,$\nabla f=\frac{\partial f}{\partial x}\vec i+\frac{\partial f}{\partial y}\vec j$。
相关概念的解释:
【📌一阶连续偏导数】对于二元函数来说,在定义域内是处处可微的(对于二元函数来说,所有方向可导,才是可微的)。也就是可以用一个过这个点的平面去近似那个点附近的曲面。(个人理解:存在过该点的切平面。)
【📌$\vec i,\vec j$】可以理解为$(1,0)$和$(0,1)$两个基向量,构成一个二维平面坐标系。
2.1.梯度与方向导数
- 方向导数是一个数值,即是一个标量。
- 梯度是一个向量,梯度的方向指向函数值(即上述定义中的$z$值)增加最快的方向,梯度的模就是方向导数的最大值。
2.2.梯度的证明
2.1部分中有关梯度的性质 是怎么来的呢?证明方法见下:
已知方向导数:$\frac{\partial f}{\partial l}=\frac{\partial f}{\partial x}\cos \varphi+\frac{\partial f}{\partial y}\sin \varphi$
如果设$\vec e=\cos \varphi \vec i+\sin \varphi \vec j$是与方向$l$(即射线$l$的方向)同方向的单位向量:
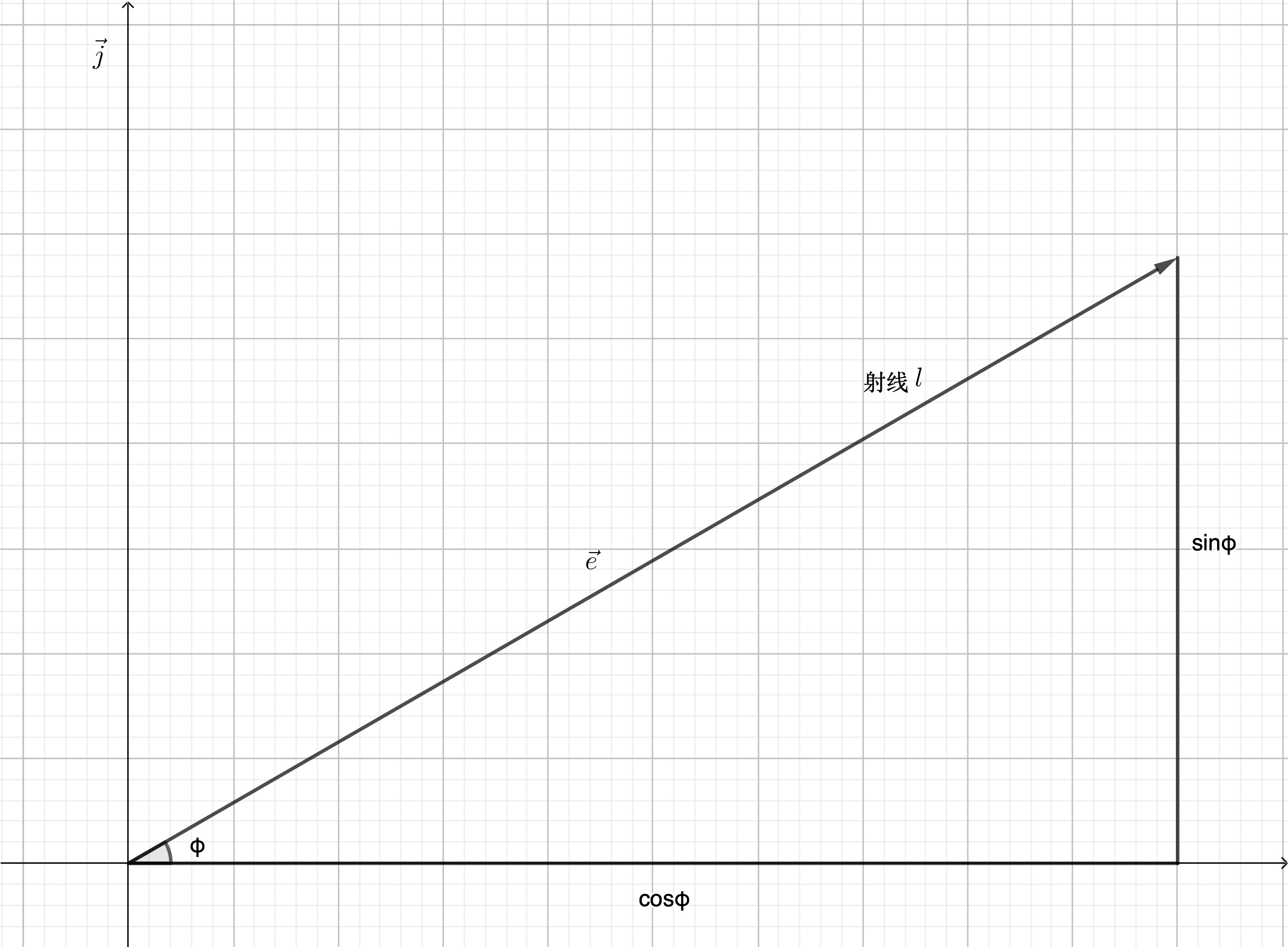
\[\begin{align} \frac{\partial f}{\partial l} & = \frac{\partial f}{\partial x}\cos \varphi +\frac{\partial f}{\partial y}\sin \varphi \tag{1} \\ & = \{ \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \} \cdot \{ \cos \varphi ,\sin \varphi \} \tag{2} \\&= gradf(x,y) \cdot \vec e \tag{3} \\&= \mid gradf(x,y) \mid \cdot \mid \vec e \mid \cdot \cos <gradf(x,y),\vec e> \tag{4} \\&= \mid gradf(x,y) \mid \cdot \cos <gradf(x,y),\vec e> \tag{5} \end{align}\]单位向量:是指模等于1的向量。
$(\sin \varphi)^2+(\cos \varphi)^2=1$
式(2)中涉及向量的点积,即:
$\vec a=(a_1,a_2,…,a_n)$
$\vec b=(b_1,b_2,…,b_n)$
$\vec a \cdot \vec b=a_1b_1+a_2b_2+,…,+a_nb_n$式(4)中,$\cos <\vec a,\vec b>$表示向量a和向量b夹角的cos值。
当方向$l$与梯度的方向一致时,有$cos <gradf(x,y),\vec e>=1$,$\frac{\partial f}{\partial l}$取得最大值,即$\mid gradf(x,y) \mid$,也就是说梯度的方向是函数$f(x,y)$在这点增长最快(即斜率最大)的方向。
2.3.梯度下降法
所谓梯度下降法就是沿着梯度的反方向,可以以最快的速度达到函数的最小值:
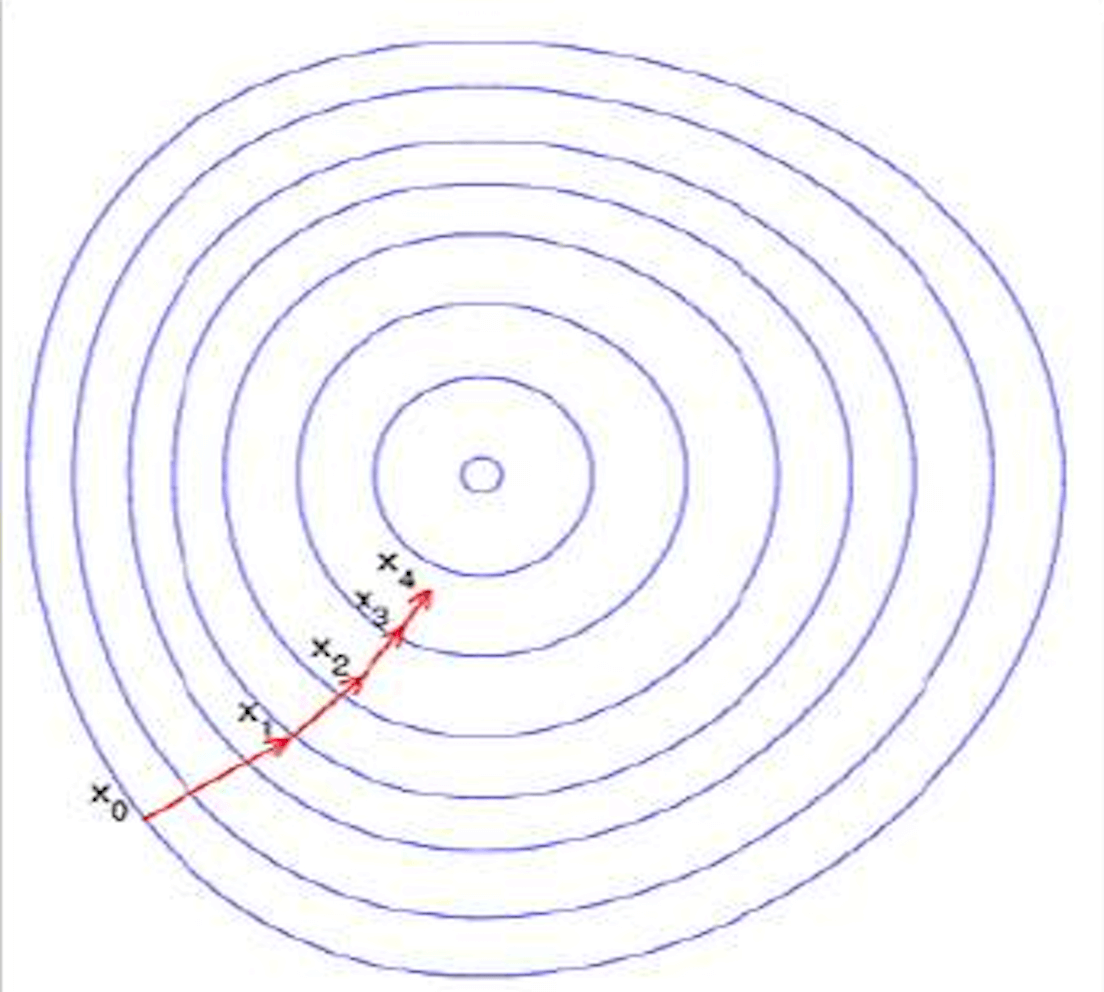
(图片来源:最优化理论梯度下降法)
梯度下降法:如果函数$f(x)$是个多元函数,$x$是一个向量,在$x_0$处对$f$做线性逼近:
\[f(x_0+\Delta x)=f(x_0)+\Delta^T_x \cdot \nabla f(x_0)+o(\mid \Delta x \mid)=g(\Delta x)+o(\mid \Delta x \mid)\]举个例子:
$f(x,y)=x^2+y^2,(x_0,y_0)=(1,1)$
$\nabla f=[2x_0,2y_0]=[2,2]$
在$(1,1)$附近有:
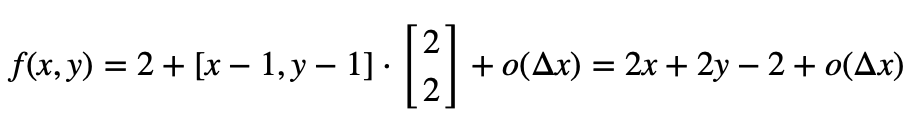
❗️梯度下降法不能告诉我们极值点在什么地方,只能告诉我们极值点在什么方向(区别于牛顿法)。
3.牛顿法
梯度下降法采用一阶逼近,而牛顿法采用二阶逼近。
以一元牛顿法为例(即只有一个变量,在$x=x_0$处展开):
\[f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f^{(2)}(x_0)}{2}(x-x_0)^2+o((x-x_0)^2)=g(x)+o((x-x_0)^2)\]$g(x)$为二次函数,函数图像为抛物线:
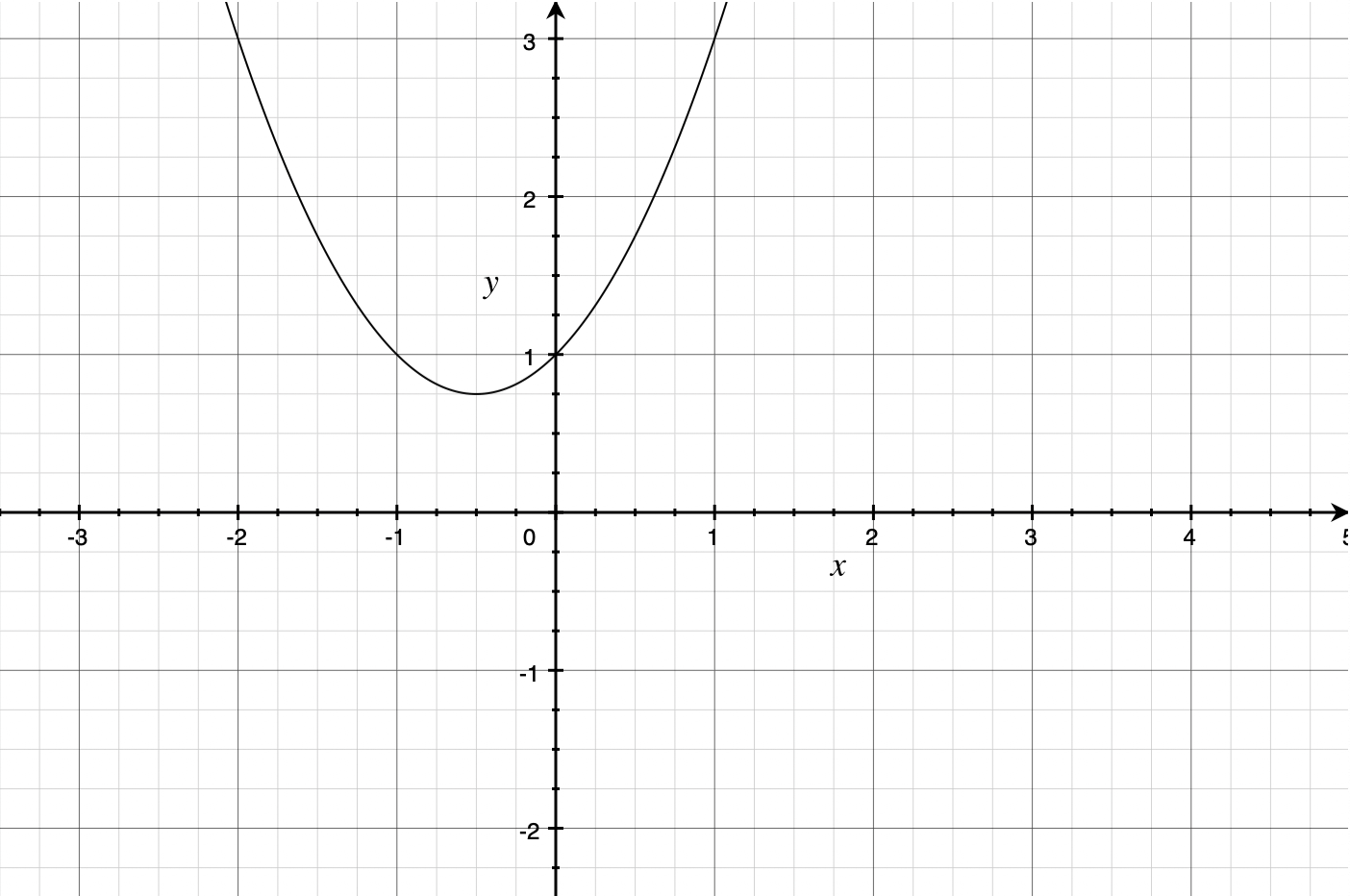
若二次项系数大于0,图像见下,此时有最小值:
若二次项系数小于0,图像见下,此时有最大值:
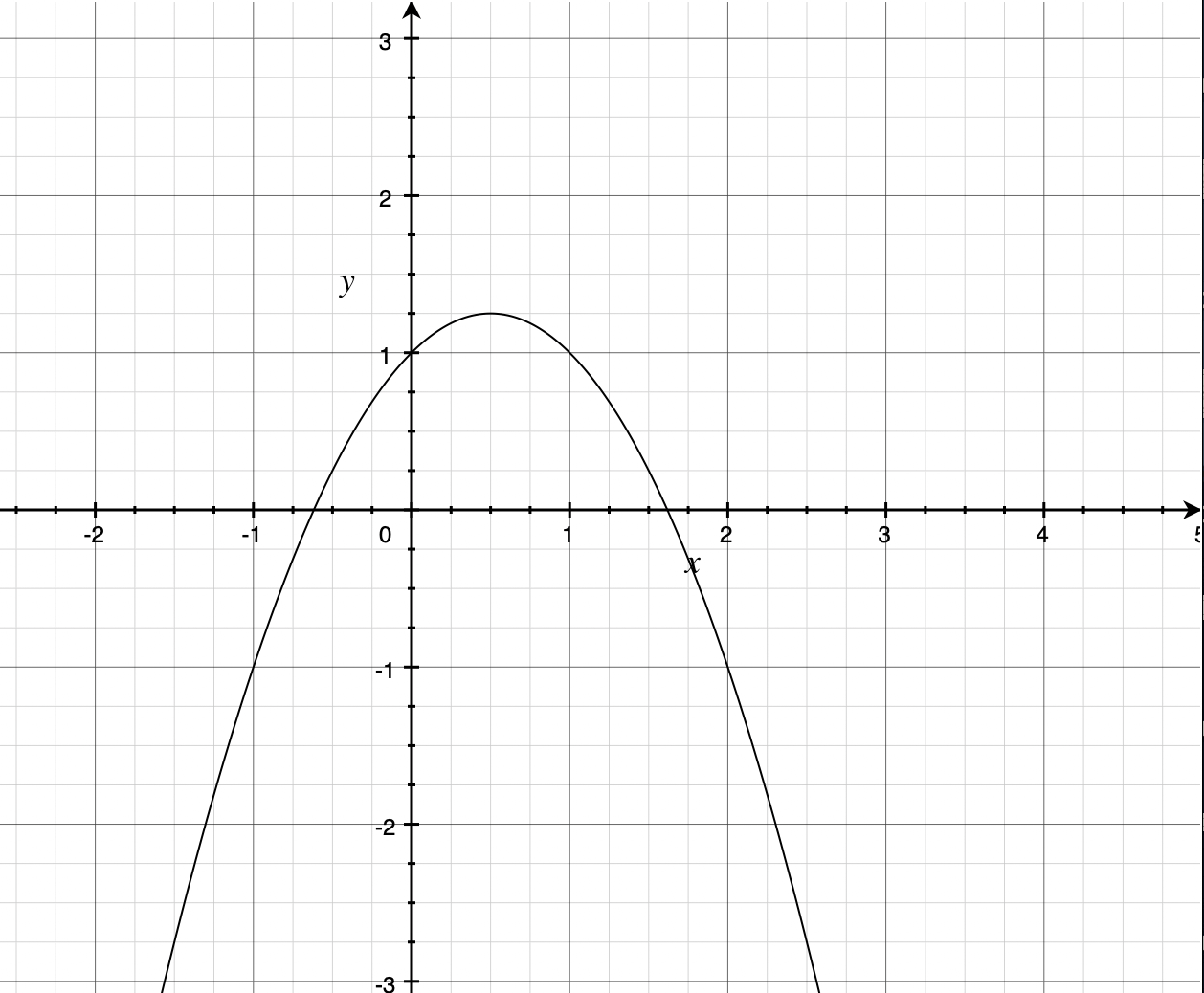
相关知识补充:
二次函数:$y=ax^2+bx+c(a\neq 0)$
二次函数的图像为抛物线,且关于y轴或平行于y轴的直线对称。
抛物线的顶点坐标:$x=- \frac{b}{2a};y=\frac{4ac-b^2}{4a}$
据上可知,$f(x)$的极值点估计在$x_1=x_0-\frac{f’(x_0)}{f^{(2)}(x_0)}$,可推广至:$x_n=x_{n-1}-\frac{f’(x_{n-1})}{f^{(2)}(x_{n-1})}$,直至收敛。
4.梯度下降法和牛顿法的异同
- 都只能寻找局部极值(不能寻找全局最小值)。
- 都必须给一个初始点$x_0$(需要避开使二阶导等于0或黑塞矩阵不可逆的点)。
- 从数学原理上,梯度下降法使用一阶逼近,牛顿法使用二阶逼近。
- 牛顿法对局部凸的函数找到极小值,对局部凹的函数找到极大值,对局部不凸不凹的可能会找到鞍点。
- 梯度下降法一般不会找到最大值,但是同样可能会找到鞍点。
- 当初始值选取合理的情况下,牛顿法比梯度下降法收敛速度快(步数更少)。
- 牛顿法要求估计二阶导数,计算难度更大。
个人理解:通常$f(x)$中的$x$为一组参数,即$x=(\theta_1,\theta_2,\theta_3,…,\theta_n)$,每组参数取值代入特定的代价函数都可得到一个总代价(即$f(x)$),因此可以通过牛顿法或者梯度下降法求得$f(x)$的局部极小值,从而也可以得到相对应的一组参数取值,最终得到最优模型。
4.1.多元梯度
\[\nabla f=[\frac{\partial f}{\partial x_1},...,\frac{\partial f}{\partial x_n}]\]4.2.多元牛顿法
\[x_n=x_{n-1}-\frac{\nabla f(x_{n-1})}{\mathbb H f(x_{n-1})}\]或:
\[x_n=x_{n-1}-\mathbb H f(x_{n-1})^{-1}\nabla f(x_{n-1})\]其中,$\mathbb H f(x_{n-1})$为Hessian矩阵(黑塞矩阵)。
4.3.鞍点
例如函数:$z=x^2-y^2$;图像见下:
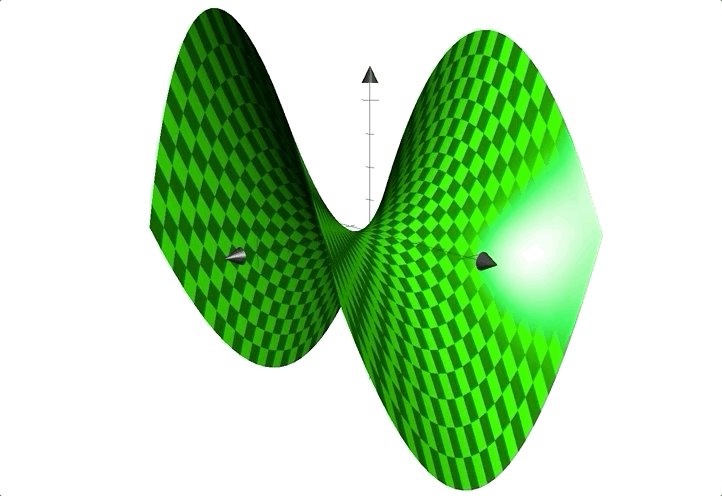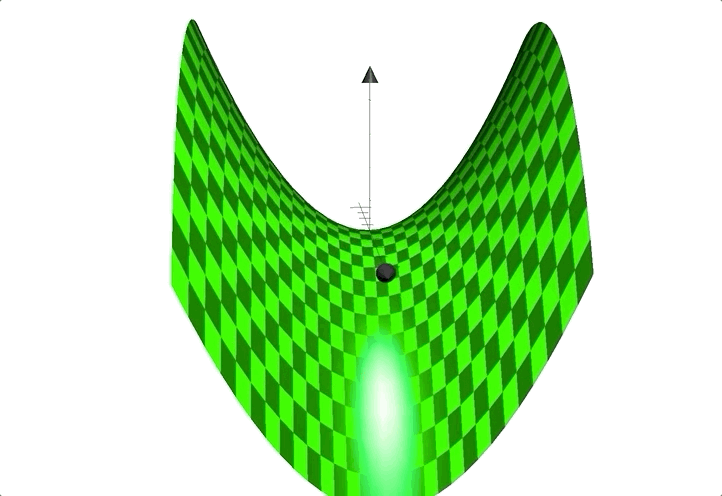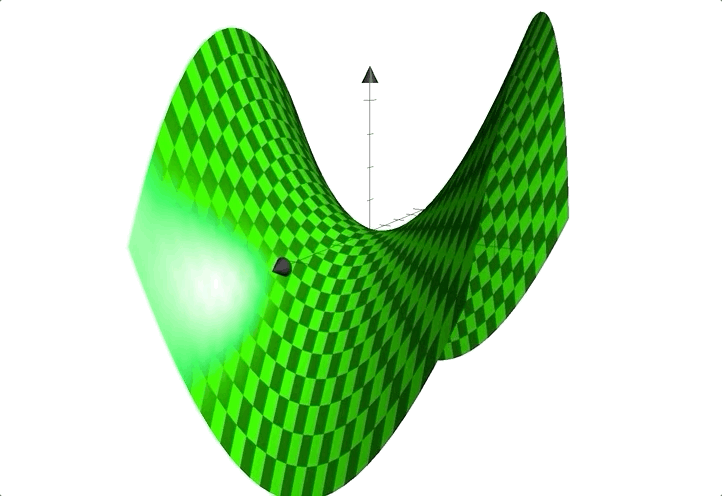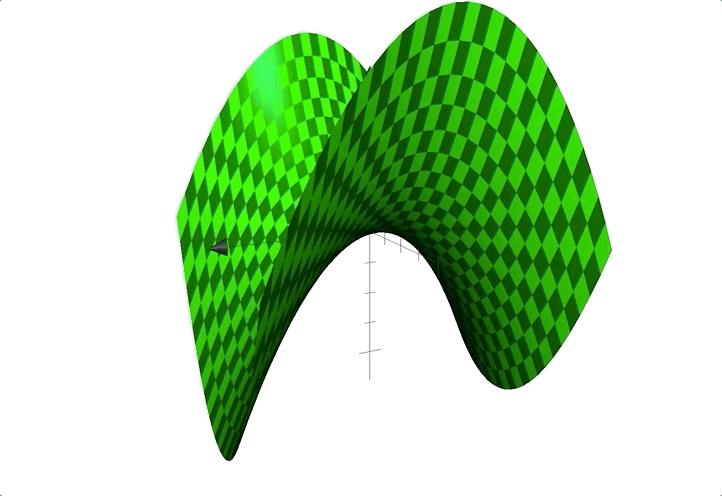
形状似马鞍,鞍点在$(0,0)$处。
❗️鞍点是临界点,却不是极值点。
4.4.Hessian Matrix
又称黑塞矩阵,是一个多元函数的二阶偏导数构成的方阵:
\[\begin{bmatrix} \frac{\partial ^2 f}{\partial x^2_1} & \frac{\partial ^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial ^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial ^2 f}{\partial x_2 \partial x_1} & \frac{\partial ^2 f}{\partial x^2_2} & \cdots & \frac{\partial ^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial ^2 f}{\partial x_n \partial x_1} & \frac{\partial ^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial ^2 f}{\partial x^2_n} \end{bmatrix}\]4.4.1.应用
👉定理:
设$n$多元实函数$f(x_1,x_2,…,x_n)$在点$M_0(a_1,a_2,…,a_n)$的邻域内有二阶连续偏导,若有:
\[\frac{\partial f}{\partial x_j} \bigg| _{(a_1,a_2,...,a_n)} = 0, j = 1,2,...,n\]并且
\[A = \begin{bmatrix} \frac{\partial ^2 f}{\partial x^2_1} & \frac{\partial ^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial ^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial ^2 f}{\partial x_2 \partial x_1} & \frac{\partial ^2 f}{\partial x^2_2} & \cdots & \frac{\partial ^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial ^2 f}{\partial x_n \partial x_1} & \frac{\partial ^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial ^2 f}{\partial x^2_n} \end{bmatrix}\]则有如下结果:
- 当A为正定矩阵时,$f(x_1,x_2,…,x_n)$在点$M_0(a_1,a_2,…,a_n)$处是极小值。
- 当A为负定矩阵时,$f(x_1,x_2,…,x_n)$在点$M_0(a_1,a_2,…,a_n)$处是极大值。
- 当A为不定矩阵时,$M_0(a_1,a_2,…,a_n)$不是极值点。
- 当A为半正定矩阵或半负定矩阵时,$M_0(a_1,a_2,…,a_n)$是“可疑”极值点,尚需要利用其他方法来判定。
👉实例:
求三元函数$f(x,y,z)=x^2+y^2+z^2+2x+4y-6z$的极值。
解:因为$\frac{\partial f}{\partial x}=2x+2,\frac{\partial f}{\partial y}=2y+4,\frac{\partial f}{\partial z}=2z-6$,故该三元函数的驻点是$(-1,-2,3)$。
又因为$\frac{\partial^2 f}{\partial x^2}=2,\frac{\partial^2 f}{\partial y^2}=2, \frac{\partial^2 f}{\partial z^2}=2, \frac{\partial^2 f}{\partial x \partial y}=0,\frac{\partial^2 f}{\partial x \partial z}=0, \frac{\partial^2 f}{\partial y \partial z}=0$,
故有:
\[A = \begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ \end{bmatrix}\]因为A是正定矩阵,故$(-1,-2,3)$是极小值点,且极小值$f(-1,-2,3)=-14$。