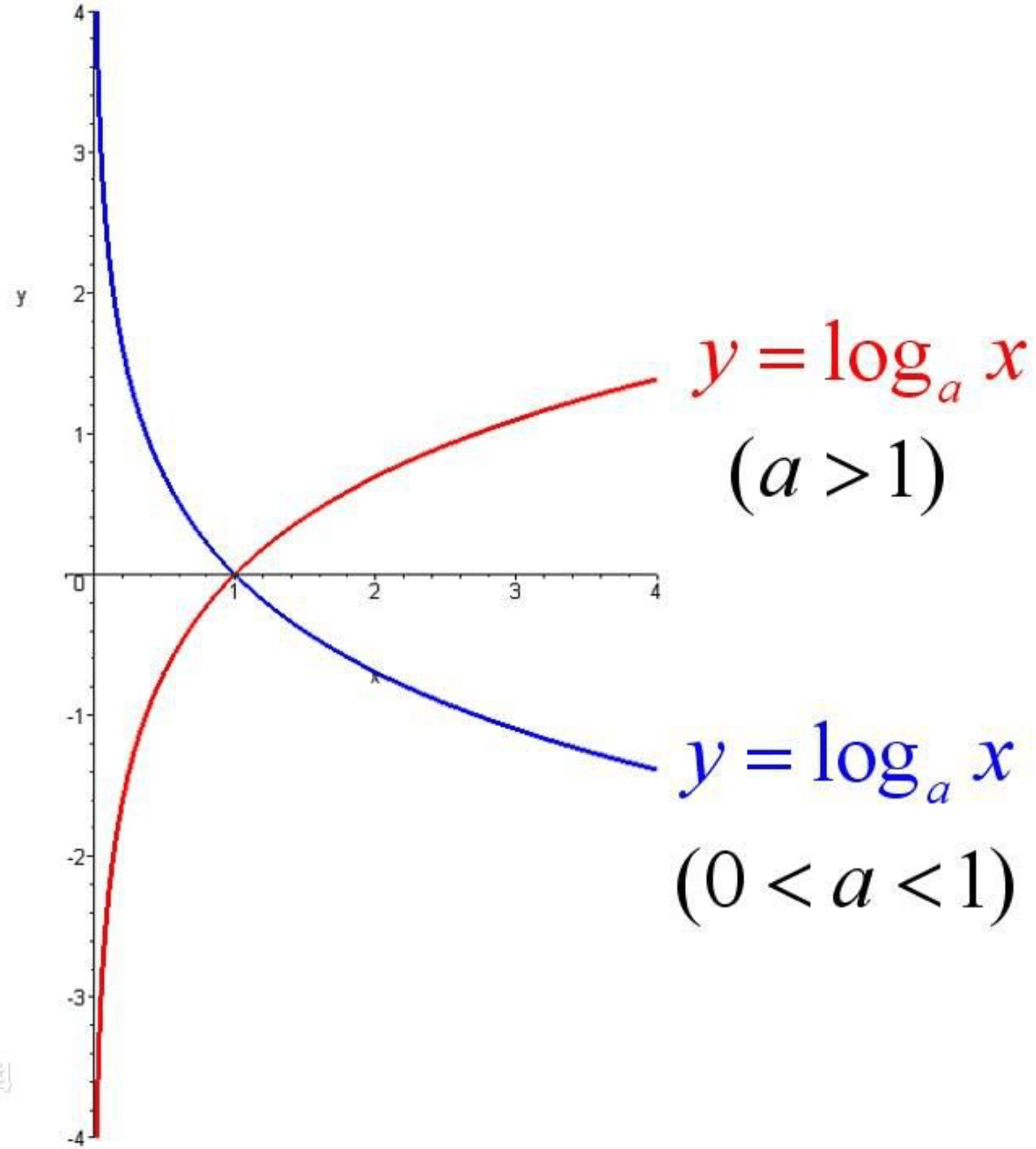【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.对数几率回归
【机器学习基础】第六课中讨论了如何使用线性模型进行回归学习,但若要做的是分类任务该怎么办?答案就是广义线性模型。
考虑二分类任务,其输出标记$y \in \{0,1\}$,而线性回归模型产生的预测值$z=\mathbf w^T \mathbf x+b$是实值,于是,需将实值$z$转换成$0/1$值,最理想的是“单位阶跃函数”(unit-step function),亦称Heaviside函数:
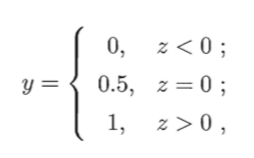
即若预测值$z$大于零就判为正例,小于零则判为反例,预测值为临界值零则可任意判别:
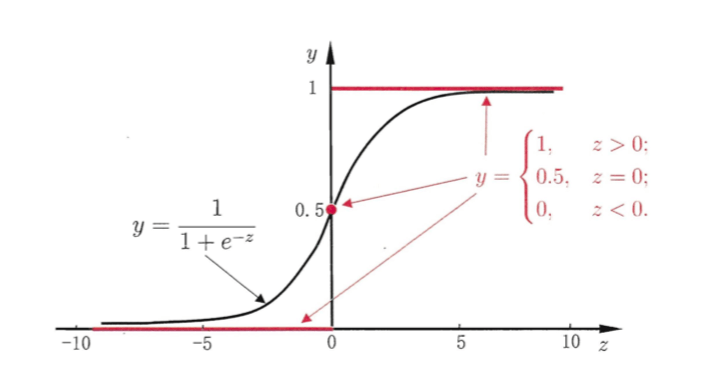
可以看出单位阶跃函数不连续,因此不能直接用作$g^-(\cdot)$,于是希望能在一定程度上近似单位阶跃函数“替代函数”,并希望它单调可微。对数几率函数(简称“对率函数”,logistic function)(⚠️对率函数和对数函数不同)正是这样一个常用的替代函数:
\[y=\frac{1}{1+e^{-z}} \tag{1}\]从上图中可以看出,对率函数是一种“sigmoid” 函数,并且其输出值在$z=0$附近变化很陡。
Sigmoid函数即形似S的函数,对率函数是Sigmoid函数最重要的代表。
将式(1)中的$z$代入:
\[y=\frac{1}{1+e^{-(\mathbf w^T \mathbf x+b)}} \tag{2}\]式(2)可变为:
\[\ln \frac{y}{1-y}=\mathbf w^T \mathbf x+b \tag{3}\]若将y视为样本$\mathbf x$作为正例的可能性,则1-y是其反例可能性,则两者的比值:
\[\frac{y}{1-y}\]称为“几率”(odds),反映了$\mathbf x$作为正例的相对可能性,对几率取对数则得到“对数几率”(log odds,亦称logit) :
\[\ln \frac{y}{1-y}\]上述模型就称为“对数几率回归”(logistic regression,亦称logit regression)。
对数几率回归译成逻辑回归(logistic regression)其实并不恰当,因为和“逻辑”(logistic)一词并无关系。
对数几率回归名字中带有“回归”二字,但实际却是一种分类学习方法。
对率函数是任意阶可导的凸函数。
2.最大似然估计
简单来说,最大似然估计(Maximum likelihood estimation,MLE)就是:
利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值。
即给定数据集$\{(\mathbf x_i,y_i)\}^m_{i=1}$,推测哪一组参数$\theta$,可以使其等于真实标记$y_i$的概率最大。
3.对数几率回归的参数估计
将式(3)中的$y$视为条件概率:
\[\ln \frac{y}{1-y}=\ln \frac{p(y=1\mid \hat{\mathbf x};\mathbf \beta)}{p(y=0\mid \hat{\mathbf x};\mathbf \beta)}=\mathbf \beta^T \hat{\mathbf x}\]其中$\mathbf \beta=(\mathbf w;b),\hat{\mathbf x}=(\mathbf x;1)$,则$\mathbf w^T \mathbf x+b$可简写为$\mathbf \beta^T \hat{\mathbf x}$。(此处可参考【机器学习基础】第六课)。
很显然可计算得到:
\[y=p(y=1\mid \hat{\mathbf x};\mathbf \beta)=\frac{e^{\mathbf \beta^T \hat{\mathbf x}}}{1+e^{\mathbf \beta^T \hat{\mathbf x}}} \tag{3.1}\] \[1-y=p(y=0\mid \hat{\mathbf x};\mathbf \beta)=\frac{1}{1+e^{\mathbf \beta^T \hat{\mathbf x}}} \tag{3.2}\]采用“极大似然法”来估计$\mathbf w,b$。给定数据集$\{(\mathbf x_i,y_i)\}^m_{i=1}$,对率回归模型最大化“对数似然”(log-likelihood):
\[\ell (\mathbf w,b)=\sum ^m_{i=1} \ln p(y_i \mid \hat{\mathbf x_i} ; \beta) \tag{3.3}\]连乘操作易造成下溢,所以通常使用对数似然(log-likelihood)。
式(3.3)中,只有$\beta$是未知的。即令每个样本属于其真实标记的概率越大越好。
对数函数图像:
对数计算法则:
- $\log_a(MN)=\log_aM+\log_aN$
- $\log_a(\frac{M}{N})=\log_aM-log_aN$
- $\log_aM^n=n\log_aM$
令:
- $p_1(\hat{\mathbf x};\mathbf \beta)=p(y=1 \mid \hat{\mathbf x} ;\mathbf \beta)$
- $p_0(\hat{\mathbf x};\mathbf \beta)=p(y=0 \mid \hat{\mathbf x} ;\mathbf \beta)=1-p_1(\hat{\mathbf x};\mathbf \beta)$
此时有:
\[p(y_i \mid \hat{\mathbf x_i};\mathbf \beta)=y_ip_1(\hat{\mathbf x_i};\mathbf \beta)+(1-y_i)p_0(\hat{\mathbf x_i};\mathbf \beta) \tag{3.4}\]当$y_i=1,p(y_i \mid \hat{\mathbf x_i};\mathbf \beta)=p_1(\hat{\mathbf x_i};\mathbf \beta)=\frac{e^{\mathbf \beta^T \hat{\mathbf x}}}{1+e^{\mathbf \beta^T \hat{\mathbf x}}}$
当$y_i=0,p(y_i \mid \hat{\mathbf x_i};\mathbf \beta)=p_0(\hat{\mathbf x_i};\mathbf \beta)=\frac{1}{1+e^{\mathbf \beta^T \hat{\mathbf x}}}$
根据式(3.1),(3.2),(3.3),(3.4)可得:
- $\ln p_1(\hat{\mathbf x_i};\mathbf \beta)=\mathbf \beta ^T\hat{\mathbf x_i}-\ln (1+e^{\mathbf \beta^T \hat{\mathbf x_i}}) \tag{3.5}$
- $\ln p_0(\hat{\mathbf x_i};\mathbf \beta)=-\ln (1+e^{\mathbf \beta^T \hat{\mathbf x_i}}) \tag{3.6}$
把式(3.5),(3.6)代入式(3.4)并取自然对数(⚠️log运算不会影响函数本身的单调性,并且式子中有$e$,取自然对数可以减少计算量):
\[\ln p(y_i \mid \hat{\mathbf x_i};\mathbf \beta)=y_i\mathbf \beta^T \hat{\mathbf x_i}-\ln (1+e^{\mathbf \beta^T \hat{\mathbf x_i}}) \tag{3.7}\]$y_i=1$,式(3.7)变为式(3.5)
$y_i=0$,式(3.7)变为式(3.6)
此时我们需要求得式(3.7)的最大值,对式(3.7)进行取负,改为求最小值:
\[\ell (\mathbf \beta)=\sum^m_{i=1}[-y_i\mathbf \beta^T \hat{\mathbf x_i}+\ln (1+e^{\mathbf \beta^T \hat{\mathbf x_i}})] \tag{3.8}\]这样做的原因是式(3.8)变为了高阶可导连续凸函数,这样就可以利用梯度下降法、牛顿法等求得最优解,于是就得到:
\[\mathbf \beta^*=\mathop{\arg\min} _{\mathbf \beta} \ell(\mathbf \beta)\]以牛顿法为例,其第$t+1$轮迭代解的更新公式为:
\[\mathbf\beta^{t+1}=\mathbf\beta^t-(\frac{\partial^2\ell(\mathbf\beta)}{\partial\mathbf\beta\partial\mathbf\beta^T})^{-1}\frac{\partial\ell(\mathbf\beta)}{\partial\beta}\]代入$\mathbf\beta$的一阶导和二阶导即可。