本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.概率分布
概率分布,是指用于表述随机变量取值的概率规律。事件的概率表示了一次试验中某一个结果发生的可能性大小。若要全面了解试验,则必须知道试验的全部可能结果及各种可能结果发生的概率,即随机试验的概率分布。如果试验结果用变量X的取值来表示,则随机试验的概率分布就是随机变量的概率分布,即随机变量的可能取值及取得对应值的概率。根据随机变量所属类型的不同,概率分布取不同的表现形式。
⚠️概率分布指的是随机变量【所有】可能的取值以及其概率。
几种常见的概率分布:
- 离散型分布:两点分布,二项分布,泊松分布。其随机变量为离散型随机变量,即值可以逐个列举出来。
- 连续型分布:均匀分布,指数分布,正态分布。其随机变量为连续型随机变量,即值无法逐个列举出来。
1.1.离散型分布
1.1.1.伯努利分布
只有两个可能结果的试验,记这两个可能的结果为0和1,下面的定义就是建立在这类试验基础上的。
如果随机变量X只取0和1两个值,并且对应的概率为(其中$0<p<1$):
- $\Pr(X=1)=p$
- $\Pr(X=0)=1-p$
则称随机变量X服从参数为p的伯努利分布(Bernoulli distribution),又称两点分布。
若令$q=1-p$,则X的概率函数可写为:
\[f(x \mid p) = \begin{cases} p^xq^{1-x}, & \text{x=0,1;} \\ 0, & \text{x≠0,1.} \end{cases}\]👉期望:
\[E(X)=1 \cdot p+0\cdot q=p\]👉方差:
\[Var(X)=E(X^2)-[E(X)]^2=1^2\cdot p+0^2\cdot q-p^2=pq\]1.1.2.二项分布
二项分布,即重复n次的伯努利试验,试验之间互相独立。
如果独立重复抛10次硬币,正面朝上的次数k可能为0,1,2,3,4,5,6,7,8,9,10中的任何一个,那么k显然是一个随机变量,这里就称随机变量k服从二项分布。
概率函数为:
\[b(k,n,p)=C^k_n p^k q^{n-k}\]其中:
- n为独立实验的次数,如独立重复抛硬币10次。
- k为事件发生的次数,如硬币正面朝上的次数。
- p为事件发生的概率,如一次独立试验中硬币正面朝上的概率。
二项分布图像示例:
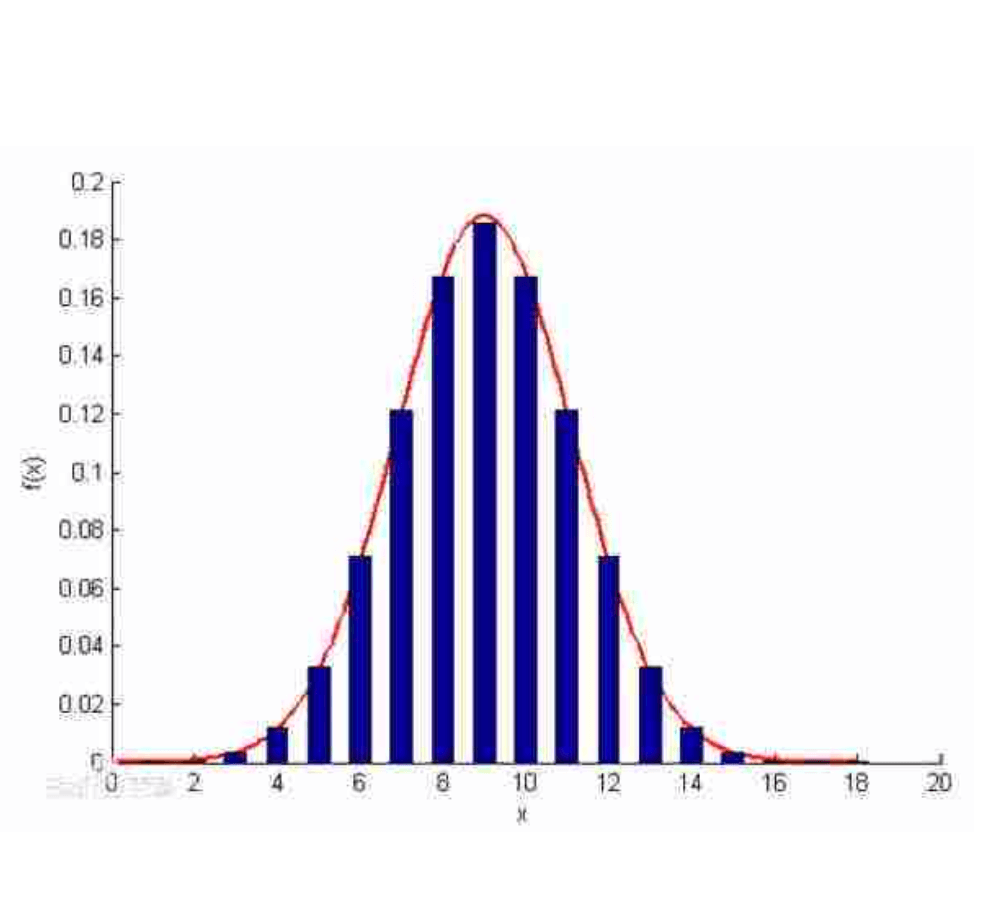
👉期望:np
👉方差:npq
1.1.3.泊松分布
❗️泊松分布适合描述【单位时间】内随机事件发生的次数的概率分布。
⚠️二项分布中如果n足够大,而p趋近于0时,二项分布趋近于泊松分布。证明见下:
\[\begin{align} \lim \limits_{n \to \infty , p \to 0} C^k_n p^k (1-p)^{n-k} & = \lim \limits_{n \to \infty , p \to 0} \frac{n(n-1)\cdots (n+1-k)}{k!} p^k (1-p)^{n-k} \tag{1.1} \\&= \lim \limits_{n \to \infty , p \to 0} \frac{n^k}{k!} p^k (1-p)^{n-k} \tag{1.2} \\&= \lim \limits_{n \to \infty , p \to 0} \frac{\lambda^k}{k!} (1-p)^{\frac{\lambda}{p}-k} \tag{1.3} \\&= \lim \limits_{n \to \infty , p \to 0} \frac{\lambda^k}{k!} [(1-p)^{\frac{1}{-p}}]^{-\lambda} \frac{1}{(1-p)^k} \tag{1.4} \\&= \lim \limits_{n \to \infty , p \to 0} \frac{\lambda^k}{k!} e^{-\lambda} \tag{1.5} \end{align}\]对上述推导过程的一些解释:
- 式(1.2):因为$n\to \infty$,所以有$\lim \limits_{n\to \infty} n(n-1)\cdots (n+1-k)=n^k$。
- 式(1.3):设$\lambda=np$,且$\lambda$为常数。
- 式(1.4):
- $\lim \limits_{p\to 0} \frac{1}{(1-p)^k}=1$。
- 因为$\lim \limits_{x\to \infty}(1+\frac{1}{x})^x=e$,所以有$\lim \limits_{p\to 0}(1-p)^{\frac{1}{-p}}=e$,其中$x=-\frac{1}{p}$。
因此,泊松分布的概率函数为:
\[p(k,\lambda)=\frac{\lambda^k}{k!}e^{-\lambda}\]其中,$\lambda >0,k=0,1,2,…,n$。
👉期望:$\lambda$
👉方差:$\lambda$
1.1.3.1.关于$\lambda$的解释
👉关于$\lambda=np$的解释:
在特定时间段内(假设特定时间段长度$t=1$),如果将该时间段平均分成n份,可以用$\frac{\lambda}{n}$($\lambda$为常数)代表在这$\frac{t}{n}$的极小的一个时间段内事件发生的概率p。因为当n趋于无穷大时,每个$\frac{t}{n}$时间段内几乎不可能有事件发生,即p趋向于0,$\frac{\lambda}{n}$($\lambda$为常数)也趋向于0。p近似地与$\frac{t}{n}$极小时间段的长度成正比。因此有$p=\frac{\lambda t}{n}=\frac{\lambda}{n}$,即$\lambda=np$。
‼️$\lambda$表示了该事件在指定时间段发生的频度(即平均频数)。例如,每周3次违章,每分钟诞生1个婴儿等。可以理解为特定时间段(比如t)内,事件平均发生$\lambda$次。即进行n次试验(n表示将时间段t平均分成n份),事件发生的期望。
1.1.3.2.泊松分布的应用
泊松分布的概率函数可以写成两种不同的形式:
- 公式1:$p=\frac{\lambda^k}{k!}e^{-\lambda}$,即我们之前一直在讨论的形式。
- 公式2:$p=\frac{(\lambda t)^k e^{-\lambda t}}{k!}$。
接下来通过一个实际的例子来看下两种形式的不同:
假设一家医院1个小时出生3个婴儿,那么接下来2个小时,一个婴儿都不出生的概率为多少?
\[p=\frac{(3\times2)^0e^{-3\times 2}}{0!}\approx 0.0025\]如果对应公式1,则$\lambda=2\times 3=6$。$\lambda$像1.1.3.1部分中所说的,为特定时间段(此处为2个小时)内,事情平均发生的次数(即2个小时内应出生6个婴儿,$\lambda=6$)。
如果对应公式2,则$\lambda =3,t=2$。$\lambda$为单位时间内事情发生的次数,即1个小时出生的婴儿数,因此$\lambda=3$,t表示单位时间的个数。
1.2.连续型分布
1.2.1.均匀分布
概率密度函数为:
\[p(x) = \begin{cases} \frac{1}{b-a}, & a\leqslant x \leqslant b \\ 0, & \text{others} \end{cases}\]其中$a<b$,且a,b均为常数。
⚠️注意:这里用的是概率密度函数,并不是之前离散型分布中的概率函数,相关区分请见本文第2部分。
👉期望:$\frac{a+b}{2}$
👉方差:$\frac{(b-a)^2}{12}$
均匀分布的概率密度函数图像和概率分布函数(累积分布函数)的图像见下:
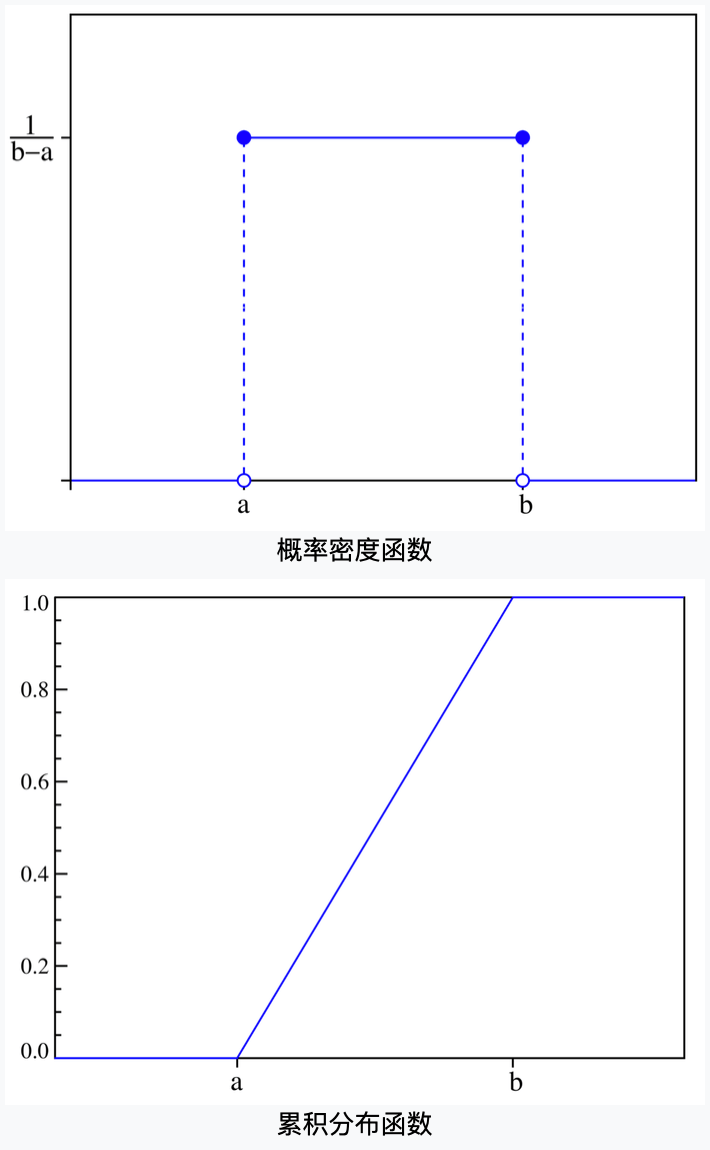
1.2.2.正态分布
若随机变量X服从一个位置参数为$\mu$,尺度参数为$\sigma$的概率分布,且其概率密度函数为:
\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma ^2}}\]则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作$X\sim N(\mu,\sigma ^2)$,读作X服从$N(\mu,\sigma ^2)$,或X服从正态分布。
👉期望:$\mu$
👉方差:$\sigma^2$
⚠️当$\mu=0,\sigma=1$时,正态分布就称为标准正态分布。
正态分布的概率密度函数图像见下:
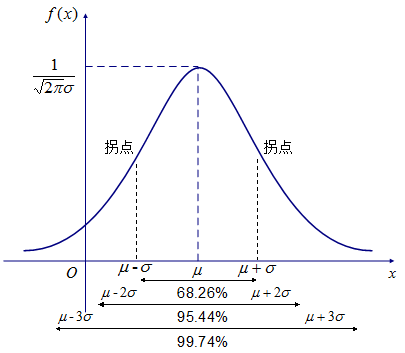
‼️当实验次数n变的非常大,几乎可以看成连续时,二项分布和泊松分布都可以近似看作正态分布。
正态分布的概率分布函数:
\[F(x)=\frac{1}{\sqrt{2\pi} \sigma}\int_{-\infty}^xe^{-\frac{(t-\mu)^2}{2\sigma ^2}}dt\]1.2.3.指数分布
‼️指数分布是描述泊松过程中的事件之间的时间的概率分布。
即距离下次事件发生的时间间隔为随机变量,其对应的概率分布。
指数分布是gamma分布的一个特殊情况。
概率密度函数:
\[f(x) = \begin{cases} \lambda e^{-\lambda x}, & {x>0} \\ 0, & {x\leqslant 0} \end{cases}\]其中$\lambda >0$是分布的一个参数,常被称为率参数。即每单位时间内发生某事件的次数(和1.1.3.2部分公式2中的$\lambda$是一个意思)。
指数分布的概率分布函数函数推导过程:
根据1.1.3.2部分公式2,泊松分布的概率函数为:$p=\frac{(\lambda t)^k e^{-\lambda t}}{k!}$。如果单位时间内事件未发生,则有$k=0$,代入求得:$p=e^{-\lambda t}$。反过来,若单位时间内有事件发生:$p=1-e^{-\lambda t}$,即指数分布的概率分布函数。对t求导,就得到其概率密度函数,即$\lambda e^{-\lambda t}$,和前文的公式一致。
👉举个应用实例:
假设一家医院1个小时出生3个婴儿,那么接下来15分钟到30分钟,会有婴儿出生的概率为:
\[\begin{align} p(0.25\leqslant X \leqslant 0.5) & = p(X\leqslant 0.5)-p(X \leqslant 0.25) \\& = (1-e^{-3\times 0.5})-(1-e^{-3\times 0.25}) \\& \approx 0.2492 \end{align}\]👉期望:$\frac{1}{\lambda}$
指数分布概率密度函数的期望可以理解为预期事件发生的间隔时间。即这次事件发生后,下次事件预期多久后会发生。
👉方差:$\frac{1}{\lambda ^2}$
2.概率函数、概率密度函数、概率分布函数
2.1.概率函数
概率函数是针对离散型概率分布来说的。
根据概率函数可以求得离散型随机变量取某一值时的概率。
2.2.概率密度函数
概率密度函数是针对连续型概率分布来说的。
根据概率密度函数可以求得连续型随机变量取某一值时的概率密度。
如下图中的(b)所示:
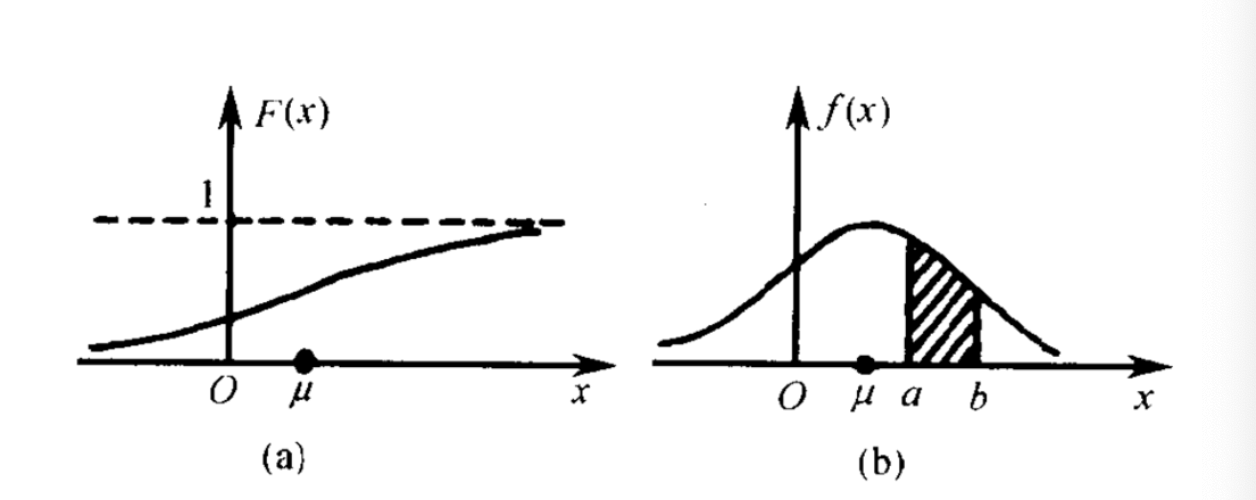
上图(b)中,a,b为连续型随机变量的取值,$f(x)$为概率密度。
此时,概率=区间$\times$概率密度。即上图(b)中阴影部分的面积表示连续型随机变量$a\leqslant X \leqslant b$时的概率。
类似于质量=体积$\times$密度
2.3.概率分布函数
⚠️注意区分【概率分布】和【概率分布函数】。
2.3.1.离散型随机变量的概率分布
对于离散型随机变量,设$x_1,x_2,…,x_n$为变量X的取值,而$p_1,p_2,…,p_n$为对应上述取值的概率,则离散型随机变量X的概率分布为:
\[P(X=x_i)=p_i,i=1,2,...,n\]且满足$\sum_{i=1}^np_i=1$。因此,离散型随机变量X的概率分布函数为:
\[F(x)=P(X\leqslant x)=\sum_{x_i \leqslant x}p_i\]其实概率分布函数就是概率函数取值的累加结果,因此又叫累积概率函数。
2.3.2.连续型随机变量的概率分布
对于连续型随机变量,设变量X取值区间为(a,b),并假设其概率分布函数$F(x)$为单调增函数,且在$-\infty < x < \infty$间可微分及其导数$F’(x)$在此区间连续,则变量X落在x至$(x+\Delta x)$区间内的概率为:
\[P(x\leqslant X \leqslant x+\Delta x)=F(x+\Delta x)-F(x)\]为描述其概率分布规律,这时不可能用分布列表示,而是引入“概率密度函数”$f(x)$的新概念。定义概率分布函数$F(x)$的导数$F’(x)$为概率密度函数$f(x)$,即:
\[f(x)=F'(x)=\lim \limits_{\Delta x\to 0}\frac{F(x+\Delta x)-F(x)}{\Delta x}\]于是连续型随机变量X的概率分布函数可写为常用的概率积分公式的形式:
\[F(x)=\int_{-\infty}^x f(x)dx\]$F(x)$图像见2.2部分图(a)。
有时称概率密度函数$f(x)$的图像为分布曲线,概率分布函数$F(x)$的图像为累积分布曲线。
因此也可求得X落在某一区间$(x_1,x_2)$内的概率:
\[P(x_1\leqslant X \leqslant x_2)=F(x_2)-F(x_1)=\int_{x_1}^{x_2}f(x)dx\]与离散型随机变量的概率函数一样,对于概率密度函数,有:
\[f(x)\geqslant 0,\int_{-\infty}^{\infty}f(x)dx=1\]