【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章，未经本人允许，禁止转载。转载请注明出处。

1.前言

向量化(vectorization)可以消除代码中显式的for循环，大大提升代码的运行效率。

因此，只要有可能，就尽量避免在代码中使用显式的for循环。

2.什么是向量化

假设有：$z=w^Tx+b$，其中，

我们看下在python代码中，分别使用非向量化和向量化两种方法计算z时的差异。

👉使用非向量化的方法：

1
2
3
4
z=0
for i in range n :
	z+=w[i]*x[i]
z+=b

👉使用向量化的方法：

1
2
import numpy as np
z=np.dot(w,x)+b

下面通过一个更加直观的例子来看下向量化和非向量化两种方式的效率：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
a = np.random.rand(1000000) #构建1000000维的数组a
b = np.random.rand(1000000) #构建1000000维的数组b

tic = time.time()
c = np.dot(a,b) #向量化方法
toc = time.time()
print(c)
print("Vectorized Version : " + str(1000*(toc-tic)) + "ms")

c = 0
tic = time.time()
for i in range(1000000) :
    c += a[i]*b[i] #使用for循环，非向量化方法
toc = time.time()
print(c)
print("for loop : " + str(1000*(toc-tic)) + "ms")

输出结果见下：

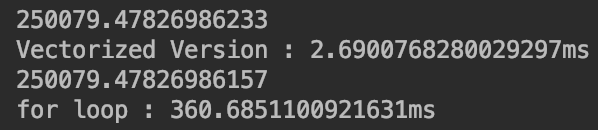
首先确保两种方法的输出结果c都是一样的。

从结果中可以明显看出，向量化方法的效率比非向量化高很多。因为numpy隐去了显式的for循环，并充分利用了并行化。这个特点对于在CPU和GPU上运算都是成立的。

2.1.更多的例子

👉假设向量v：

求v的指数：

非向量化的方法：

1
2
3
u = np.zeros((n,1))
for i in range(n):
	u[i]=math.exp(v[i])

向量化的方法：

1
2
import numpy as np
u = np.exp(v)

numpy中其他的类似用法：

1. u=np.log(v)
2. u=np.abs(v)
3. u=np.maximum(v,0) #返回v中每个元素和0之间的最大值
4. v**2 #计算v中每个元素的平方
5. 1/v #计算v中每个元素的倒数

3.使用向量化实现logistic回归梯度下降算法

根据之前博客【深度学习基础】第四课：正向传播与反向传播中所讲的计算logistic回归中梯度的算法：

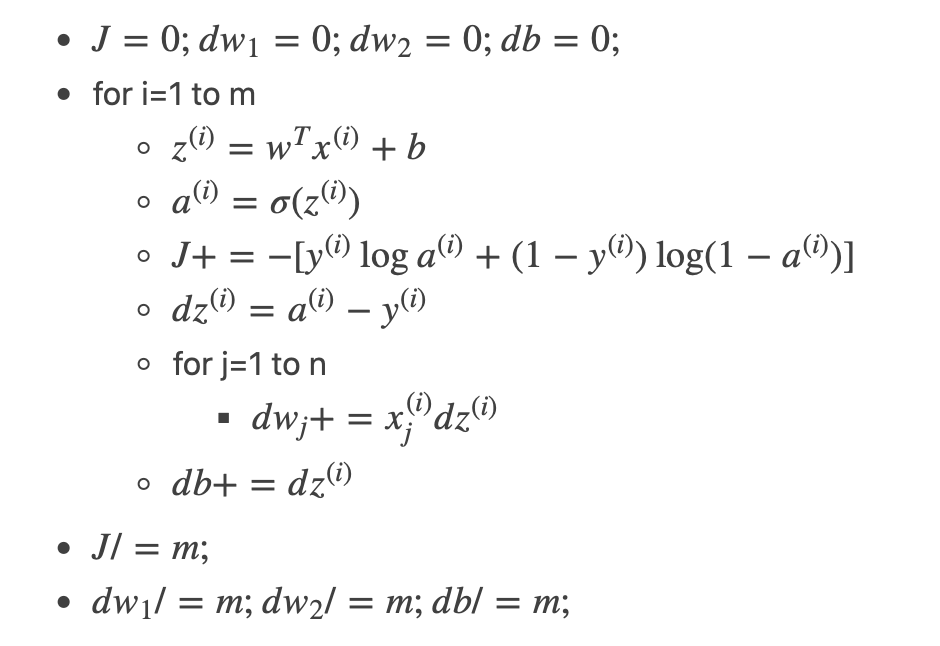
这里有两个显式for循环。

👉现在向量化第一个for循环：

定义$Z=[z^{(1)},z^{(2)},…,z^{(m)}]$，则有：

即：$Z=w^T X+b$。可使用numpy将上式写为：Z=np.dot(w.T,X)+b。

❗️在实际运算时，numpy会将实数b扩展为$[b,b,…,b]$，这个操作在python中叫做广播(broadcasting)。

同理，我们可以定义$A=[a^{(1)},a^{(2)},…,a^{(m)}]$，然后将$Z$作为sigmoid函数的输入，输出为A。

同时定义$dZ=[dz^{(1)},dz^{(2)},…,dz^{(m)}];Y=[y^{(1)},y^{(2)},…,y^{(m)}]$，因此有：$dZ=A-Y$。

👉同样的，我们也可以将第二个for循环向量化：

首先将$dw_1,dw_2,…,dw_n$初始化为一个向量dw：dw=np.zeros((n,1))。然后可以把第二个for循环向量化为：$dw+=x^{(i)} dz^{(i)}$，在消去第一个for循环后即为：$dw=X \cdot dZ^T$。

但是其中还有对$dw,db$中各元素累加求和然后求平均的过程，这也需要对m个样本做一个遍历。同样也可以对其进行向量化：db=(1/m)* np.sum(dZ)、dw=(1/m)* np.dot(X,dZ.T)。

最后，便可对参数$(w,b)$进行一次更新：$w:=w-\alpha dw$、$b:=b-\alpha db$。

到此，我们就实现了不使用任何一个显式的for循环就能利用梯度下降法完成一次参数的更新。但是，如果想要对参数进行多次更新，即多次迭代，就不得不使用一个for循环了，这个是无法避免的。

4.广播(Broadcasting)

通过几个例子来看下python中broadcasting的原理。

更加详细的介绍请查阅numpy官方文档中对broadcasting的介绍。本节所介绍的broadcasting方式是深度学习中主要用到的。

4.1.例子一

假设现在我们得到了四种食物的成分表：

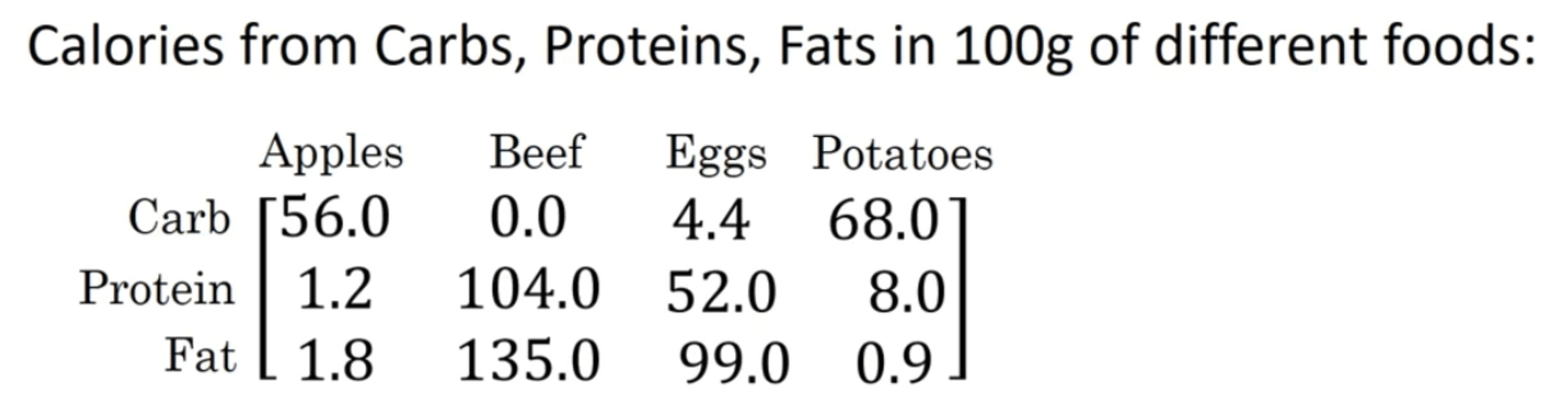
如果我们现在想要知道每种食物中碳水、蛋白质和脂肪的卡路里占比。例如苹果中碳水的卡路里占比为：$\frac{56.0}{56.0+1.2+1.8}=94.9\%$。那么我们需要做的就是用每列中的各个元素去除以对应列的和。我们尝试不使用显式的for循环来完成这个任务。

先将数据输入到数组中：

1
2
3
4
5
A = np.array([
    [56.0, 0.0, 4.4, 68.0],
    [1.2, 104.0, 52.0, 8.0],
    [1.8, 135.0, 99.0, 0.9]
])

对各列求和：

1
cal = A.sum(axis=0) #输出为：[ 59.  239.  155.4  76.9]

axis=0为各列求和；axis=1为各行求和。

计算各成分所占百分比：

1
percentage = A / cal.reshape(1,4)

调用reshape的成本很低，可以经常调用reshape以确保所用的矩阵是自己想要的尺寸。

得到最后的结果：

4.2.例子二

broadcasting会将其扩展为：

同样的，这种扩展形式也适用于行向量。

broadcasting会复制第二个矩阵的行，使之与第一个矩阵的维数相同以满足矩阵加法的条件：

类似的，

被broadcasting扩展为：

5.关于numpy中的向量

numpy在赋予编码极大灵活性的同时也容易因使用不当而造成一些不易察觉、难以调试的bug。

本节我们来简单的讲解一下如何避免使用numpy构建向量时容易出现的错误。

首先使用numpy生成5个随机高斯变量并存在数组a中：

1
2
import numpy as np
a = np.random.randn(5)

通过a.shape可以看到a的结构为(5,)，这是python中秩为1的数组，既不是行向量也不是列向量。如果此时对a做转置，即a.T，会发现a和a转置是完全一样的。

因此，在深度学习编程时，应避免使用这种(n,)秩为1的数组。我们可以通过a = np.random.randn(5,1)来构建一个维度为$5\times 1$的数组，从而避免秩为1的数组。

也可以通过设置参数keepdims=True来避免秩为1的数组。

tips:
经常使用assert来确保构建的数组是自己想要的维度（assert的执行效率很高，所以不用担心会使代码的运行速度变慢）。例如：assert(a.shape == (5,1))。

此外，也可以使用a.reshape()来转换秩为1的数组的维度。

6.代码地址

1. 向量化、logistic回归

• Previous
  【OpenCV基础】第六课：图像混合
• Next
  【C++基础】第十二课：自定义数据结构