【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.前言
目前为止,我们所用的激活函数都是sigmoid函数,但有时其他函数的效果要更好,本文将介绍其他常用的激活函数。
2.常用的激活函数
2.1.tanh函数
tanh函数又叫双曲正切函数:

有:
\[a=g(z)=\tanh (z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}\]a表示activate function,即激活函数。
可以看出,tanh函数其实就是sigmoid函数平移后的版本。
⚠️tanh函数作为激活函数的效果几乎总是比sigmoid函数的效果要好!但是有一个例外:如果输出的结果为二分类问题,则输出层可以选择sigmoid函数作为激活函数。
❗️不同层的激活函数可以不同。例如我们可以用$g^{[1]}(z^{[1]})$表示第一层的激活函数,用$g^{[2]}(z^{[2]})$表示第二层的激活函数。
⚠️但是tanh函数和sigmoid函数都存在一个很明显的缺点:当z值很大或者很小的时候,函数的斜率就会变得非常小(接近于0),这样会拖慢梯度下降算法。
2.2.ReLU函数
ReLU函数(Rectified Linear Unit, ReLU),又称修正线性单元:

公式为:$a=g(z)=max(0,z)$。
- 当z为负时,斜率为0。
- z刚好为0时,导数是不存在的。但是在实际情况中,z=0的概率非常非常低。所以在编程实现时,并不需要考虑这个问题。或者也可以当z=0时,把导数值设为0或1。
- 当z为正时,斜率为1。
‼️ReLU函数是大多数神经网络的默认激活函数。因此在不知道选择哪种函数作为激活函数时,可以优先选择ReLU函数。
⚠️ReLU函数的一个缺点就是当z<0时,导数为0。因此引入Leaky ReLU函数克服这个缺点。
2.3.Leaky ReLU函数
Leaky ReLU函数的图像见下:

公式可能为:$a=g(z)=max(0.01z,z)$。常数通常为0.01,当然也可以作为一个参数,从而根据实际情况进行调整。
⚠️Leaky ReLU的效果通常比ReLU函数要好,但是实际使用的频率并不高。
❗️ReLU函数(或Leaky ReLU函数)不会因为z值过大而导致学习速度减慢,因此以ReLU函数(或Leaky ReLU函数)作为激活函数的神经网络的学习速度通常比sigmoid函数和tanh函数快很多。
3.激活函数的选择
可以通过交叉验证的方法选择最适合的激活函数。
4.为什么需要非线性激活函数
从上述介绍可以看出,基本所有的激活函数都是非线性函数。那么神经网络为什么需要这些非线性激活函数呢?
正常的神经网络结构见下:
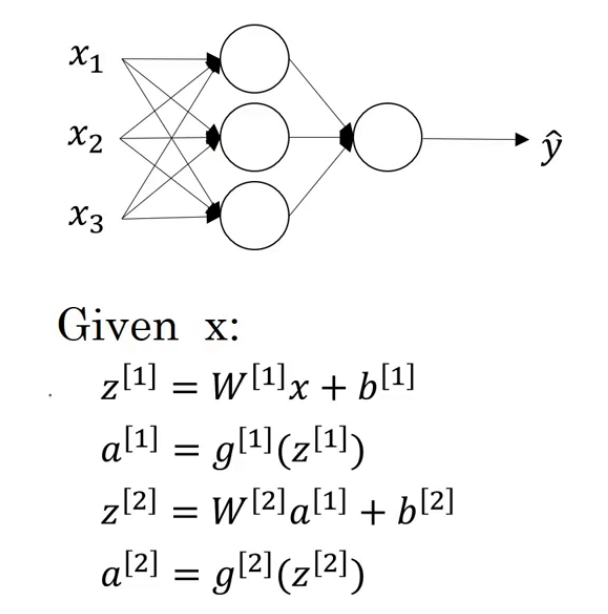
$g^{[1]}$和$g^{[2]}$为非线性激活函数,我们现在将其改为线性激活函数(也称恒等激活函数):
- $a^{[1]}=z^{[1]}=W^{[1]}x+b^{[1]} \tag{4.1}$
- $a^{[2]}=z^{[2]}=W^{[2]}a^{[1]}+b^{[2]} \tag{4.2}$
将式4.1带入式4.2:
\[\begin{align} a^{[2]} & = W^{[2]}(W^{[1]}x+b^{[1]})+b^{[2]} \\ & = (W^{[2]}W^{[1]})x+(W^{[2]}b^{[1]}+b^{[2]}) \\ & = W'x+b' \\ \end{align}\]⚠️可以看出,假设我们使用线性激活函数,那么神经网络的输出其实就是输入特征的线性组合。这种情况下,隐藏层就失去了存在的意义。
❗️只有一个地方可以使用线性激活函数:当解决回归问题时,输出层的激活函数可以为线性激活函数。
5.激活函数的导数
当进行反向传播时就需要计算激活函数的导数。
- sigmoid函数:$g’(z)=\frac{d}{dz}g(z)=g(z)(1-g(z))=a(1-a)$。
- tanh函数:$g’(z)=1-a^2$。
- ReLU函数:
- $if \ z<0,g’(z)=0$。
- $if \ z>0,g’(z)=1$。
- $if \ z=0,undefined$。但是在实际编码中,可令$g’(z)=1 \ or \ 0$(原因见2.2部分)。
- Leaky ReLU函数:
- $if \ z<0,g’(z)=0.01$(以2.3部分的公式为例)。
- $if \ z>0,g’(z)=1$。
- 同理,当z=0时,可令$g’(z)=1 \ or \ 0.01$。