本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.期望
在概率论和统计学中,数学期望是试验中每次可能结果的概率乘以其结果的总和,即概率加权下的“平均值”。
👉离散型随机变量的期望:$E(X)=\sum^\infty_{k=1} x_k p_k$
👉连续型随机变量的期望:$E(X)=\int^\infty _{-\infty}xf(x)dx$
1.1.期望的性质
设C为一个常数,X和Y是两个随机变量。以下是数学期望的重要性质:
- $E(C)=C$
- $E(CX)=CE(X)$
- $E(X+Y)=E(X)+E(Y)$
- 当X和Y相互独立时,$E(XY)=E(X)E(Y)$
❗️性质3和性质4可以推到任意有限个相互独立的随机变量之和或之积的情况。
⚠️针对性质4:若$E(XY)=E(X)E(Y)$,则X和Y不一定相互独立。举例见下:
假设随机变量Y的分布为:$P_{(Y=1)}=P_{(Y=-1)}=0.5$。当Y=1时,$P_{(X=1)}=P_{(X=-1)}=0.5$;当Y=-1时,$P_{(X=2)}=P_{(X=-2)}=0.5$。很显然X和Y不互相独立,但是:
- $E(Y)=1\times 0.5+(-1)\times 0.5=0$
- $E(X)=1\times 0.5+(-1)\times 0.5+2\times 0.5+(-2)\times 0.5=0$
- XY共有四种取值:1,-1,-2,2,概率均为0.25,可求得$E(XY)=0$
此时$E(XY)=E(X)E(Y)$,但X和Y并不相互独立。
2.方差
❗️方差的定义:
\[Var(X)=E\{ [X-E(X)]^2 \}=E(X^2)-E^2(X) \tag{2.1}\]公式推导:
\[\begin{align} Var(x) & = E\{ [X-E(X)]^2 \} \tag{2.2} \\ & = E[X^2-2XE(X)+E^2(X)] \tag{2.3} \\ & = E(X^2)-2E[XE(X)]+E[E^2(X)] \tag{2.4} \\ & = E(X^2)-2E(X)E(X)+E^2(X) \tag{2.5} \\&= E(X^2)-2E^2(X)+E^2(X) \\&= E(X^2)-E^2(X) \end{align}\]- 式2.3可利用期望的性质3展开。
- 式2.4中$E(X)$和$E^2(X)$均是一个具体的数值,可作为常数提出去,外层的$E$对其不起作用。
2.1.方差的性质
- $Var(C)=0$
- $Var(X+C)=Var(X)$
- $Var(kX)=k^2Var(X)$
- 当X和Y互相独立时,$Var(X+Y)=Var(X)+Var(Y)$
3.协方差
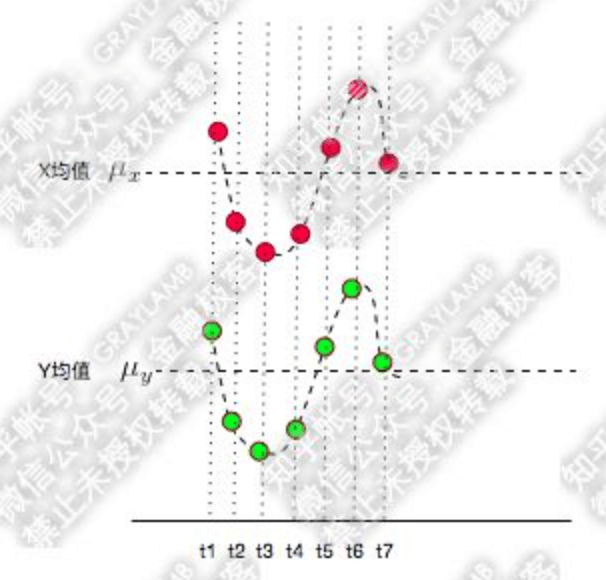
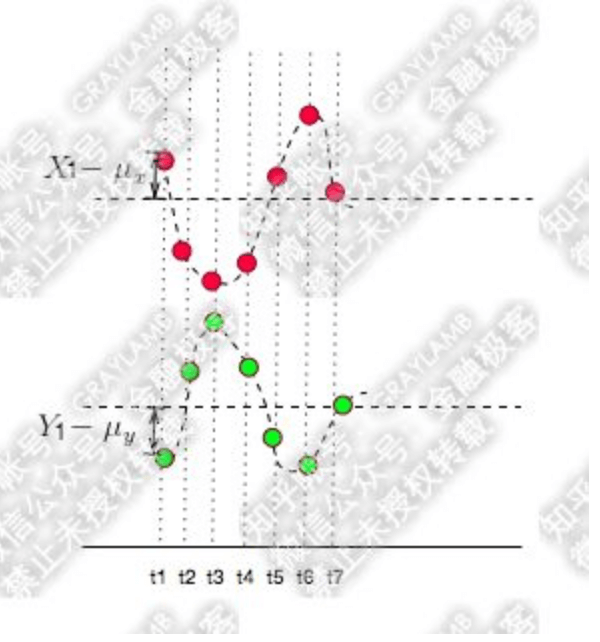
协方差表示的是两个变量的总体误差:
\[Cov(X,Y)=E\{ [X-E(X)][Y-E(Y)] \}\]- $Cov(X,Y)=0$:X和Y不相关。
- $Cov(X,Y)>0$:X和Y同向运动,值越大,同向程度越高(数量级一样,比较大小才有意义)。
- $Cov(X,Y)<0$:X和Y反向运动,值越小,反向程度越高(数量级一样,比较大小才有意义)。
虽然个别点可能会有例外,但并不影响总体:
个人理解:协方差中的X和Y通常是一一对应的关系,而不是像1.1中举的例子那样,Y的一个取值对应多个X的取值。
3.1.协方差的性质
- $Cov(X,Y)=Cov(Y,X)$
- $Cov(aX+b,cY+d)=acCov(X,Y)$
- $Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(X_2,Y)$
- $Cov(X,Y)=E(XY)-E(X)E(Y)$
‼️协方差只能评价两个变量的线性关系,无法判断非线性关系。
3.2.协方差矩阵
设$X=(X_1,X_2,…,X_N)^T$为n维随机变量(其中$X_1,X_2,…,X_N$均为随机变量),如果需要计算各维度两两之间的协方差,可构建协方差矩阵:
\[C=(c_{ij})_{n\times n}=\begin{bmatrix} c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{n1} & c_{n2} & \cdots & c_{nn} \\ \end{bmatrix}\]其中:
\[c_{ij}=Cov(X_i,X_j),i,j=1,2,...,n\]4.相关系数
⚠️协方差虽然在一定程度上能够反映X和Y之间的相关关系,但其受X和Y量纲的影响。
因此引入“相关系数”的概念,消除量纲影响。
首先对X和Y分别进行标准化处理:
\[X^*=\frac{X-E(X)}{\sqrt{D(X)}};Y^*=\frac{Y-E(Y)}{\sqrt{D(Y)}}\]其中$D(X)$和$D(Y)$为方差。
这样就将其转化为了标准化随机变量,标准化随机变量有性质:$E(X^*)=E(Y^*)=0$、$\sqrt{D(X^*)}=\sqrt{D(Y^*)}=1$。
其实也不一定必须除以标准差,这只是标准化常用的一个选择。
此时计算去量纲的协方差,即相关系数:
\[\begin{align} r(X,Y) & = Cov(X^*,Y^*) \\ & = E\{ [X^*-E(X^*)][Y^*-E(Y^*)] \} \\ & = E[\frac{X-E(X)}{\sqrt{D(X)}} \cdot \frac{Y-E(Y)}{\sqrt{D(Y)}}] \\ & = \frac{E\{ [X-E(X)][Y-E(Y)] \}}{\sqrt{D(X)} \sqrt{D(Y)}} \\&= \frac{Cov(X,Y)}{\sqrt{D(X)} \sqrt{D(Y)}} \end{align}\]‼️所以说,相关系数是一种剔除了两个变量量纲影响,即标准化后的特殊协方差。
4.1.相关系数与向量内积
假设有向量:
- $\vec{a}=(x_1-\bar x,x_2-\bar x,x_3-\bar x,…,x_n-\bar x)$,其中$\bar x=\frac{1}{n}(x_1+x_2+x_3+…+x_n)$。
- $\vec{b}=(y_1-\bar y,y_2-\bar y,y_3-\bar y,…,y_n-\bar y)$,其中$\bar y=\frac{1}{n}(y_1+y_2+y_3+…+y_n)$。
根据向量内积,有
\[\begin{align} \cos \theta & = \frac{\vec a \cdot \vec b}{\mid \vec a \mid \cdot \mid \vec b \mid} \\ & = \frac{\sum^n_{i=1}(x_i-\bar x)(y_i-\bar y)}{\sqrt{\sum^n_{i=1}(x_i-\bar x)^2} \sqrt{\sum^n_{i=1}(y_i-\bar y)^2}} \\ & = \frac{\frac{\sum^n_{i=1}(x_i-\bar x)(y_i-\bar y)}{n} }{\frac{\sqrt{\sum^n_{i=1}(x_i-\bar x)^2}}{ \sqrt{n}} \frac{\sqrt{\sum^n_{i=1}(y_i-\bar y)^2}}{\sqrt{n}}} \\ & = \frac{Cov(X,Y)}{\sqrt{D(X)} \sqrt{D(Y)}} \\&= r(X,Y) \end{align}\]4.2.相关系数的性质
- $-1\leqslant r \leqslant 1$
- $r > 0$:正相关
- $r = 0$:无相关性
- $r < 0$:负相关