本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.黎曼积分(Riemann Integral)
黎曼积分是积分学中一种比较基础且常见的积分概念。除此之外,还有勒贝格积分等。但是本文只讨论黎曼积分。
👉单变量函数黎曼积分:
令$f(x)$为开区间$(a,b)$上的一个连续函数,对于任何一个正整数$n$定义,$x_i=a+\frac{i(b-a)}{n}$求和式:
\[S_n(f)=\sum^{n-1}_{i=0}f(x_i)(x_{i+1}-x_i)\]如果极限$\lim _{n\to \infty} S_n(f)$存在,那么函数$f(x)$在这个区间上的黎曼积分为:
\[\int ^b_a f(x)dx=\lim_{n\to \infty} S_n(f)\]1.1.黎曼积分的几何意义
‼️黎曼积分的几何意义:函数与x轴之间的有向面积。
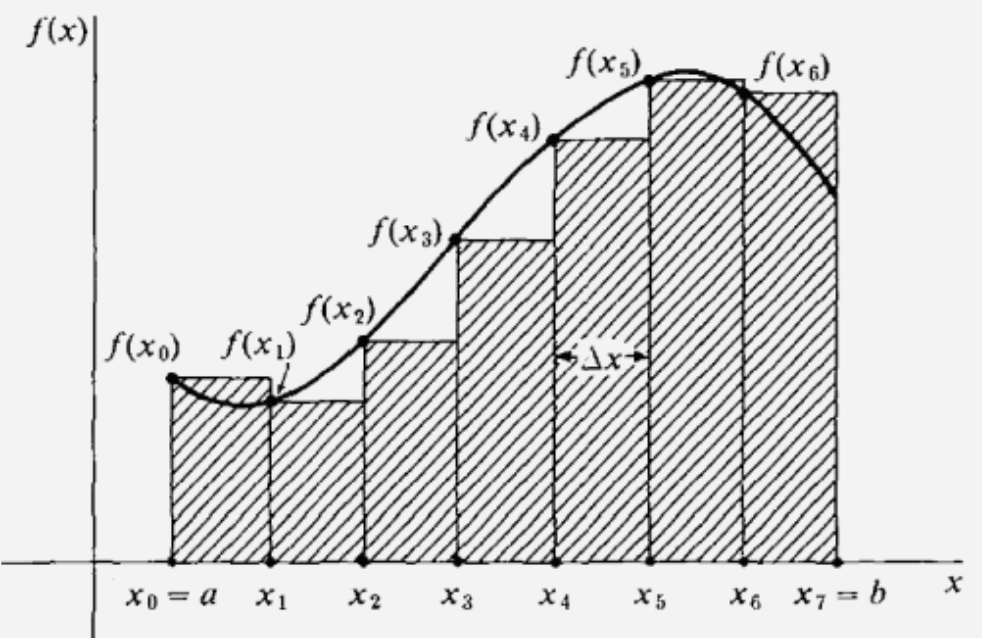
如上图所示,黎曼积分其实就是用多个矩形的面积去逼近函数曲线下面积。
上图中每个矩形的面积为$f(x_h)(x_{i+1}-x_i),x_h \in [x_{i},x_{i+1}]$。此外,每个矩形的宽度也不一定非得是相同的:
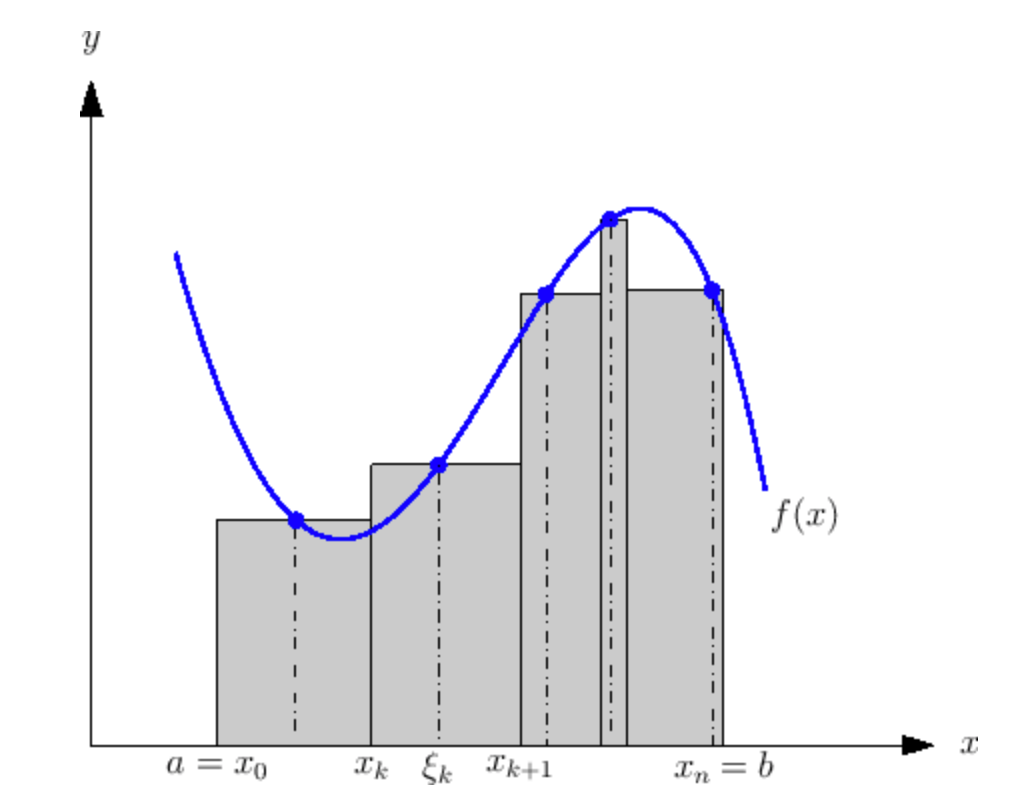
这是因为当矩形的个数趋于无限大时,得到的结果都是相同的,都是曲线下的面积。
了解了这些之后,我们再来进一步看下什么叫做有向面积。
函数与x轴之间的有向面积即下图中蓝色区域的面积减去黄色区域的面积:
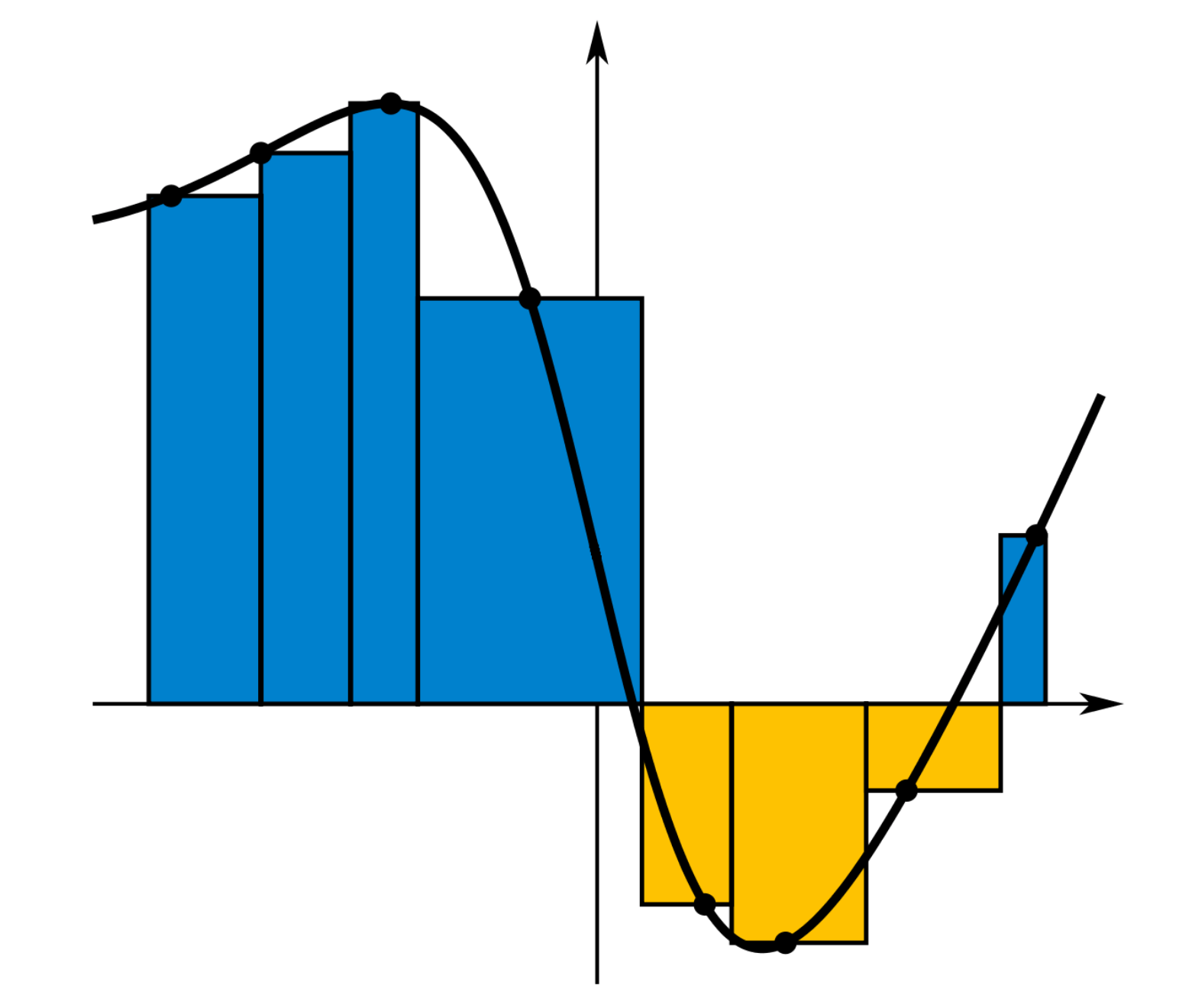
这个结合上述的公式也很好理解,因为蓝色区域部分$f(x_h)>0$,而黄色区域部分$f(x_h)<0$,并且$(x_{i+1}-x_i)$是始终大于0的。
2.牛顿-莱布尼兹公式
如果$f(x)$是定义在闭区间$[a,b]$上的可微函数,那么就有:
\[\int^b_a f'(t)dt=f(b)-f(a)\]⚠️上式为定积分形式,无常数项,有具体的范围,单纯地表示$y=f(x)$围成的图形的面积,是一个具体的数值。
👉不定积分的形式(无特定范围,需要一个常数项):
\[\int f'(t)dt=f(x)+C\]❗️牛顿-莱布尼兹公式展示了微分与积分的基本关系:在一定程度上微分与积分互为逆运算。
2.1.几何意义
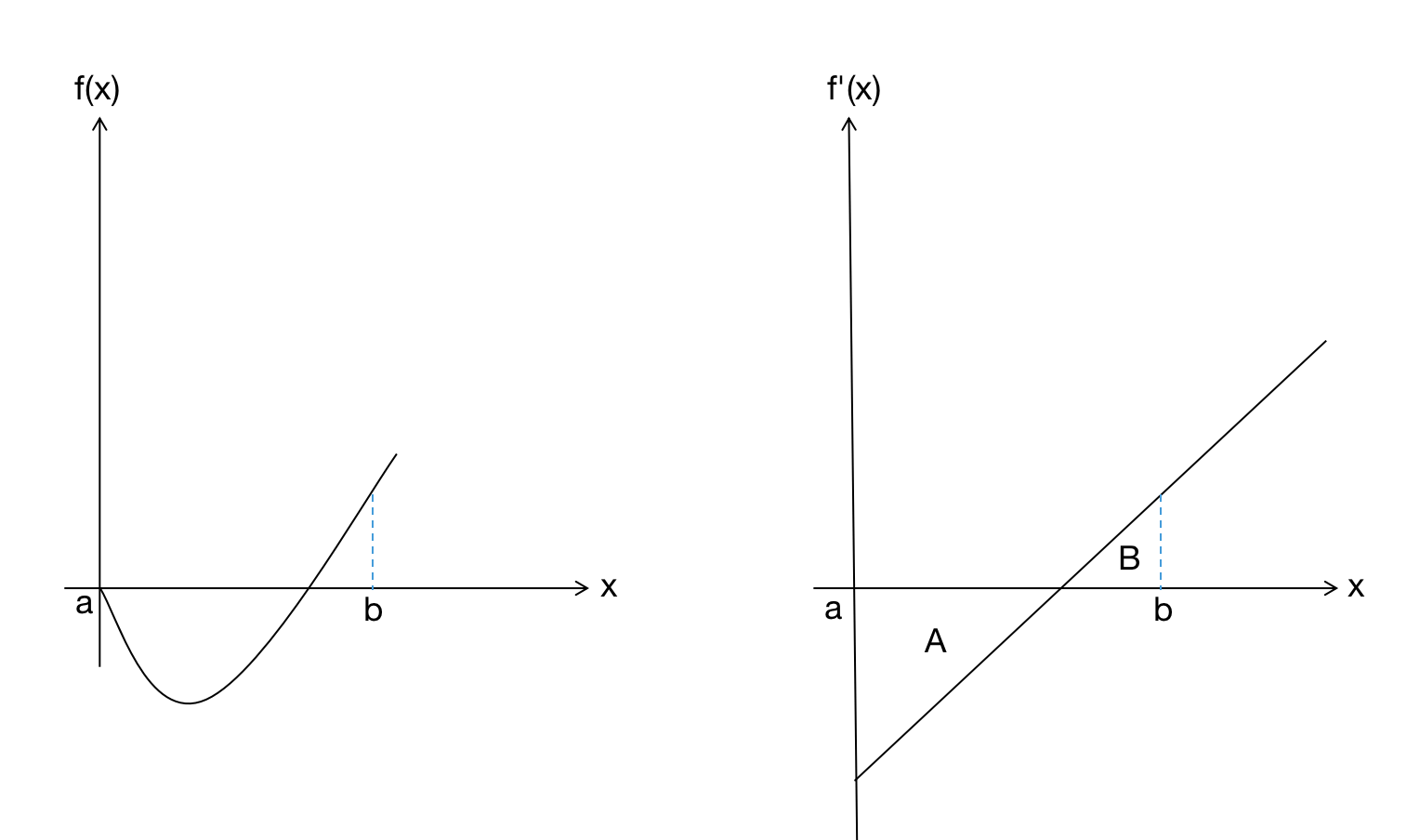
根据1.1部分,$\int ^b_a f’(x)dx$可以理解为函数与x轴之间的有向面积,即所有矩形面积的和。其中矩形的高为$f’(x)$,宽为$dx$,单个矩形的面积为$f’(x)dx$,根据微分的相关知识可知$dy=f’(x)dx$,即每个矩形的面积对应着原函数$f(x)$中$dx$所对应的增量$dy$,那么从a到b所有矩形的面积之和也就对应着$f(x)$从a到b的函数值增量之和,即$f(b)-f(a)$。因此有:
\[\int^b_a f'(t)dt=f(b)-f(a)\]2.2.分部积分法
设$u=u(x)$及$v=v(x)$是两个关于$x$的函数。
根据求导法则有:
\[(u(x)\cdot v(x))'=u'(x)\cdot v(x)+u(x)\cdot v'(x)\]对等式两边同时求不定积分:
\[\int (u(x)\cdot v(x))' dx=\int u'(x)\cdot v(x) dx+ \int u(x)\cdot v'(x) dx\]化简:
\[u(x)\cdot v(x)=\int u'(x)\cdot v(x) dx+ \int u(x)\cdot v'(x) dx\]通常写为:
\[\int u(x)\cdot v'(x) dx = u(x)\cdot v(x)-\int u'(x)\cdot v(x) dx\]上式即为分部积分法,可简写为:
\[\int uv' dx=uv-\int vu' dx\]其中$v’=\frac{dv}{dx},u’=\frac{du}{dx}$,带入上式可得:
\[\int udv=uv-\int v du\]这是分部积分法的另一种表现形式。
2.3.例题
2.3.1.例题1
\[\begin{align} \int \ln x dx & = \int d(x\ln x) - \int x d(\ln x) \\ & = x\ln x+C_1 - \int x \cdot \frac{1}{x} dx \\ & = x\ln x+C_1 - \int 1 dx \\ & = x\ln x+C_1 - (x+C_2) \\ & = x\ln x -x + C \end{align}\]2.3.2.例题2
👉换元法的使用:
\[\begin{align} \int^{\ln 3}_0 e^x \sqrt{1+e^x}dx & = \int^{\ln 3}_0 \sqrt{1+e^x}d(e^x) \\ & = \int^{\ln 3}_0 \sqrt{1+e^x} d(1+e^x) \\ & = \int^{\ln 3}_0 (1+e^x)^{\frac{1}{2}} d(1+e^x) \\ & = \frac{2}{3} (1+e^x)^{\frac{3}{2}} | ^{\ln 3}_0 \\ & = \frac{2}{3} [8-2\sqrt{2}] \end{align}\]2.3.3.例题3
计算$x^{-\alpha}$的不定积分。
当$\alpha \neq 1$时:
\[\int \frac{1}{x^{\alpha}} dx=\frac{1}{(1-\alpha)x^{\alpha -1}}+C\]当$\alpha =1$时:
\[\int \frac{1}{x^{\alpha}} dx = \int \frac{1}{x} dx=\ln x+C\]3.多变量函数的积分
\[\int^d_c \int^b_a f(x,y)dxdy\]依次从里向外积分即可。
⚠️二重积分的几何意义是积分函数与X-Y坐标平面之间部分的有向体积。