【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.为什么要正则化?
正则化可以降低模型复杂度,防止过拟合。
2.范数
$L_1$范数、$L_2$范数和$F$范数都常用于正则化。
2.1.向量的$L_p$范数
\[\parallel \mathbf x \parallel _p = (\sum^N_{i=1} \mid x_i \mid^p)^{\frac{1}{p}},p\in [0,+\infty)\]由此可得:
👉$L_1$范数:
\[\parallel \mathbf x \parallel _1 = \sum^N_{i=1} \mid x_i \mid\]👉$L_2$范数:
\[\parallel \mathbf x \parallel _2 = \sqrt {\sum^N_{i=1} x_i^2}\]2.2.矩阵的$F$范数
$F$范数全称为:Frobenius范数。
定义如下:
\[\parallel \mathbf X \parallel _F=\sqrt{\sum^m_i \sum^m_j x^2_{ij}}\]3.正则化的应用
3.1.正则化在逻辑回归中的应用
3.1.1.L2正则化
构建目标函数:
\[J(w,b)+\frac{\lambda}{2m} \parallel w \parallel ^2_2\]其中,
\[\parallel w \parallel ^2_2=\sum^{n_x}_{j=1} w^2_j\],m为样本个数,$n_x$为维数。
这种方法称为L2正则化。
当然也可以加上对参数b的正则化:
\[J(w,b)+\frac{\lambda}{2m} \parallel w \parallel ^2_2 + \frac{\lambda}{2m} b^2\]因为w通常为一个高维向量,但是b只是一个数(即只是众多参数中的一个),所以省略对b的正则化没有什么太大的影响,因此常被省去。
3.1.2.L1正则化
类似的,也存在L1正则化方法:
\[J(w,b)+\frac{\lambda}{2m} \parallel w \parallel _1\]👉但是在实际训练模型时,人们通常倾向于选择L2正则化。
3.1.3.超参数$\lambda$
可以看出,无论是L1正则化还是L2正则化,都含有超参数$\lambda$。
3.1.4.L1正则化和L2正则化的区别
- L1正则化更适用于特征选择。
- L2正则化更适用于防止模型过拟合。
下面从梯度下降法的角度探讨一下这种区别的原因。
为了简化,假设数据只有两个特征$w_1,w_2$。
👉L1正则化:$J+\frac{\lambda}{2m}(\mid w_1 \mid + \mid w_2 \mid)$
在每次更新$w_1$时:
\[\begin{align} w_1 : & = w_1 - \alpha dw_1 \\ & = w1 - \alpha (\frac{\partial J}{\partial w_1}+\frac{\lambda}{2m} sign(w_1)) \\&= w1-\alpha \frac{\partial J}{\partial w_1} - \frac{\alpha \lambda}{2m} sign(w_1) \end{align}\]数学符号:sign
当x>0时,sign(x)=1
当x=0时,sign(x)=0
当x<0时,sign(x)=-1
若$w_1$为正数,则每次更新会减去一个常数;若$w_1$为负数,则每次更新会加上一个常数,所以很容易产生特征的系数为0的情况,特征系数为0表示该特征不会对结果有任何影响,因此L1正则化会让特征变得稀疏,起到特征选择的作用。
👉L2正则化:$J+\frac{\lambda}{2m}(w_1^2+w_2^2)$
在每次更新$w_1$时:
\[\begin{align} w_1 : & = w_1 - \alpha dw_1 \\&= w_1 - \alpha (\frac{\partial J}{\partial w_1}+\frac{\lambda}{m}w_1) \\&= (1-\frac{\alpha \lambda}{m})w_1 - \alpha \frac{\partial J}{\partial w_1} \end{align}\]其中,设定合适的超参数$\lambda$,让$0<(1-\frac{\alpha \lambda}{m})<1$。
从上式可以看出每次更新时,会对$w_1$进行特定比例的缩小,防止系数过大从而让模型变得复杂,避免过拟合,而不会起到特征选择的作用。因此L2正则化也称为权重衰减(weight decay)。
一般认为权值较小的模型比较简单,能适应不同的数据集,也能在一定程度上避免过拟合现象。因为当权值很大的时候,只要数据有一点点的偏移,就会对结果造成很大的影响,从而导致模型对新数据的适应能力很差。
3.2.正则化在神经网络中的应用
因为在神经网络中,w通常为一个矩阵,因此我们使用F范数用于正则化,其目标函数为:
\[J(w^{[1]},b^{[1]},...,w^{[L]},b^{[L]})+\frac{\lambda}{2m} \sum^L_{l=1} \parallel w^{[l]} \parallel ^2_F\]其中,
\[\parallel w^{[l]} \parallel ^2_F = \sum^{n^{[l]}}_{i=1} \sum^{n^{[l-1]}}_{j=1} (w^{[l]}_{ij})^2\]在每次更新$w^{[l]}$时:
\[\begin{align} w^{[l]} : & = w^{[l]} - \alpha dw^{[l]} \\&= w^{[l]} - \alpha (\frac{\partial J}{\partial w^{[l]}} + \frac{\lambda}{m} w^{[l]}) \\&= (1-\frac{\alpha \lambda}{m})w^{[l]} - \alpha \frac{\partial J}{\partial w^{[l]}} \end{align}\]和L2正则化基本相同,可参照3.1.4部分。
4.为什么正则化可以减少过拟合?
我们已经在3.1.4部分讨论了为什么正则化可以避免过拟合。这里我们通过两个例子来进一步的说明。
👉第一个例子:
以3.2部分的正则化应用为例,当$\lambda$足够大时,会有$w^{[l]} \approx 0$,可直观的理解为把多个隐藏神经元的权重设为0(或者接近于0),于是基本消除了这些隐藏神经元的许多影响。因此一个大的神经网络会被简化成一个很小的网络:
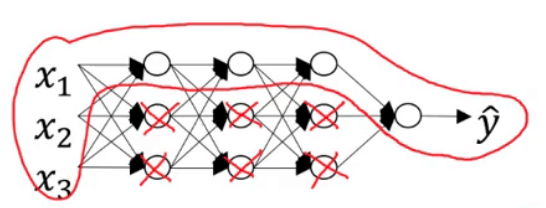
上述操作会使得模型从下图最右侧的状态逐渐变为最左侧的状态:
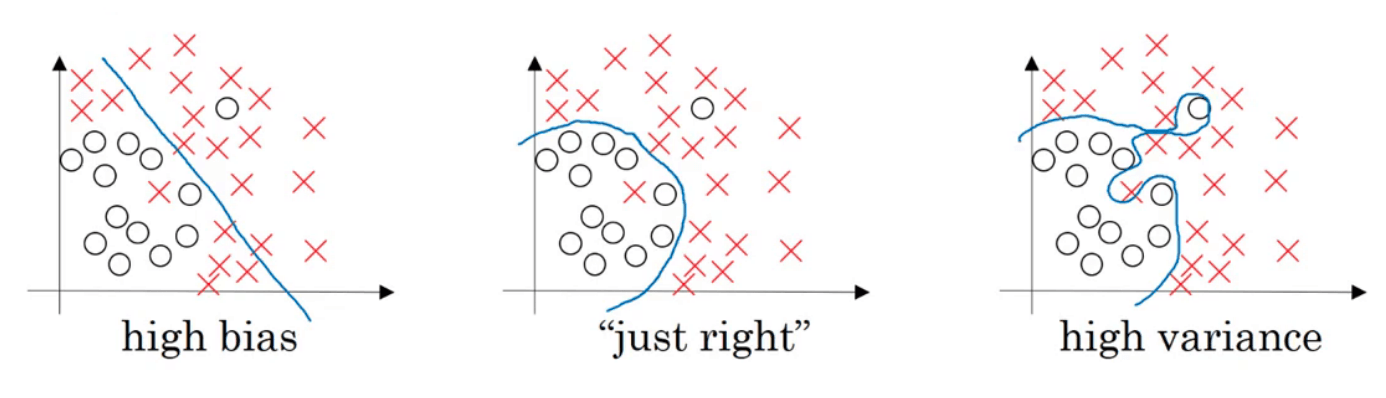
但是总会存在一个合适的$\lambda$,使得模型正好处于上图中中间模型的状态。
👉第二个例子:
以tanh激活函数为例。
当$\lambda$增大时,$w^{[l]}$变小,又$z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}$,因此$z^{[l]}$也会变小。当$\lambda$取值合适时,tanh函数会被简化为线性激活函数(如下图红线部分所示):

我们在【深度学习基础】第七课:激活函数中提到过,如果每层都是线性激活函数,那么网络中的隐藏层便失去了意义,整个网络被简化成一个线性模型。
5.Dropout正则化
除了使用F范数,dropout也是神经网络中非常实用的一种正则化方法。
我们来看一下dropout的工作原理。
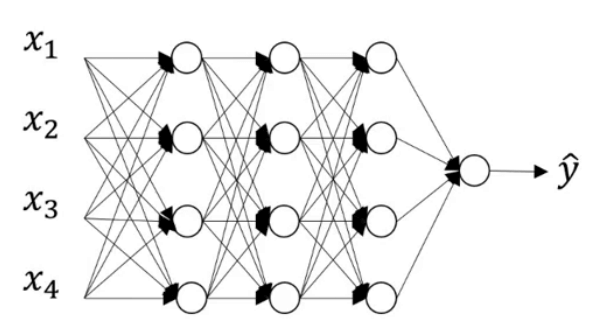
假设上图中的模型存在过拟合现象。dropout会遍历网络的每一层并设置消除神经网络中节点的概率。假设每个节点得以保留和消除的概率都为0.5,我们会得到一个节点更少,规模更小的网络:
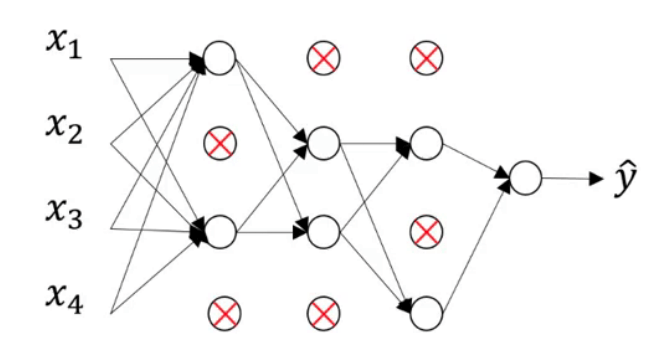
对于每一个样本,都会执行一次dropout,所以说对每个样本来说,网络中被隐藏的节点可能是不同的。
5.1.Inverted Dropout
以某一层(假设为第l层)的inverted dropout为例。
1
dl=np.random.rand(al.shape[0],al.shape[1])<keep_prob
其中,keep_prob是预先设置好的阈值,表示保留某个隐藏神经元的概率。上述语句得到的dl是一个矩阵,矩阵里面的元素为True或者False。
1
al=np.multiply(al,dl) #也可写为:al*=dl
np.multiply为两个同型矩阵对应的元素相乘。
python会把矩阵
dl中的true和false翻译成1和0。
然后对al进行扩展:
1
al /= keep_drop
⚠️这一步是inverted dropout和dropout的区别所在。inverted dropout相比dropout多了这一步。
这是因为当我们在继续计算$z^{[l+1]}=w^{[l+1]}a^{[l]}+b^{[l+1]}$时,$a^{[l]}$中有(1-keep_drop)比例的元素被归零,因此我们对$a^{[l]}$进行了扩展,以确保$a^{[l]}$的期望值是不变的,从而不影响$z^{[l+1]}$的期望值。
这里只介绍了inverted dropout在前向传播中的应用,其在后向传播中的应用是一样的,这里不再赘述。
‼️目前实施dropout最常用的方法就是inverted dropout。
5.1.1.keep_prob的设置
‼️每一层的keep_prob可以不同。但是也会因此产生很多超参数需要提前设置。
- 对于容易产生过拟合的层(即权重矩阵$w^{[l]}$比较大的层),
keep_prob的阈值可以设置的偏低一些。 - 对于不容易产生过拟合的层(即权重矩阵$w^{[l]}$比较小的层),
keep_prob的阈值可以设置的偏高一些。 - 对于不会产生过拟合的层,可设置
keep_prob=1。
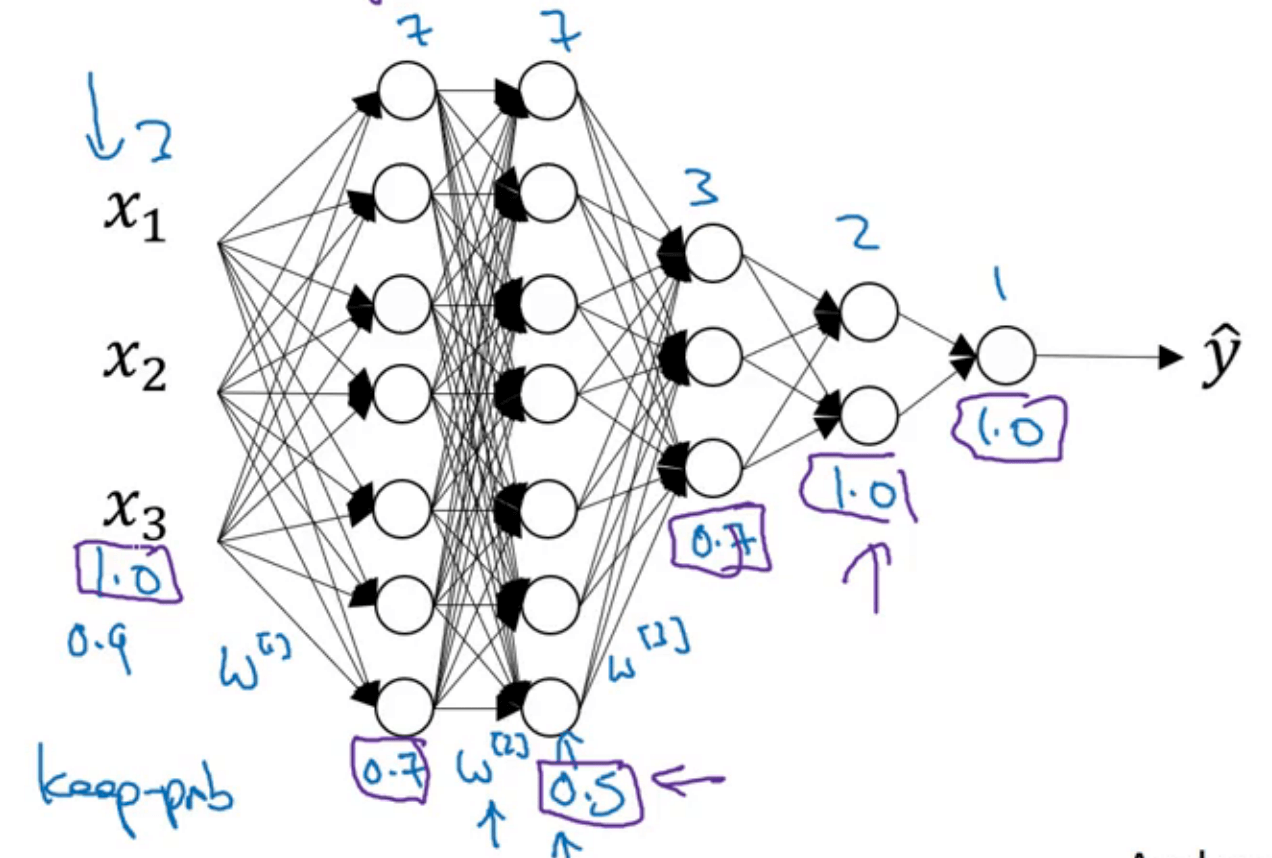
上图中每层的keep_prob用紫色方框标示出来。
⚠️dropout也可应用于输入层。但是输入层的keep_prob应该接近于1,不能太小。
5.2.测试阶段
⚠️在测试阶段不使用dropout函数。
如果测试阶段应用dropout函数,预测会受到干扰。
6.其他正则化方法
6.1.data augmentation
可以通过对原始训练集中的数据进行扩展(比如裁剪;旋转;反转等),从而避免过拟合:
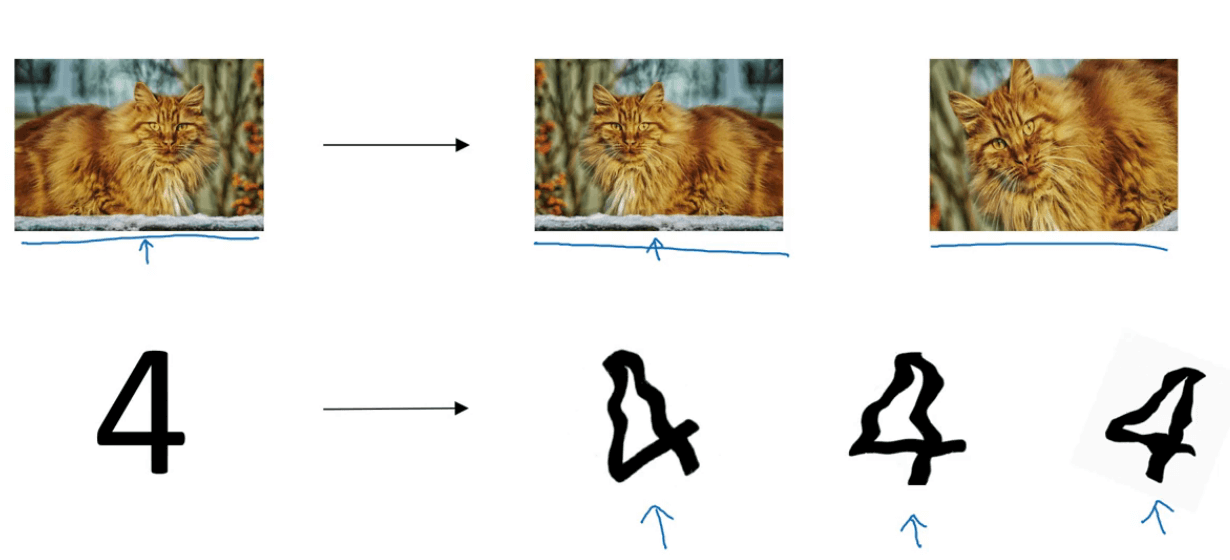
推荐一个好用的图像扩展的python库:imgaug。
6.2.early stopping
early stopping意味着提早停止训练神经网络。
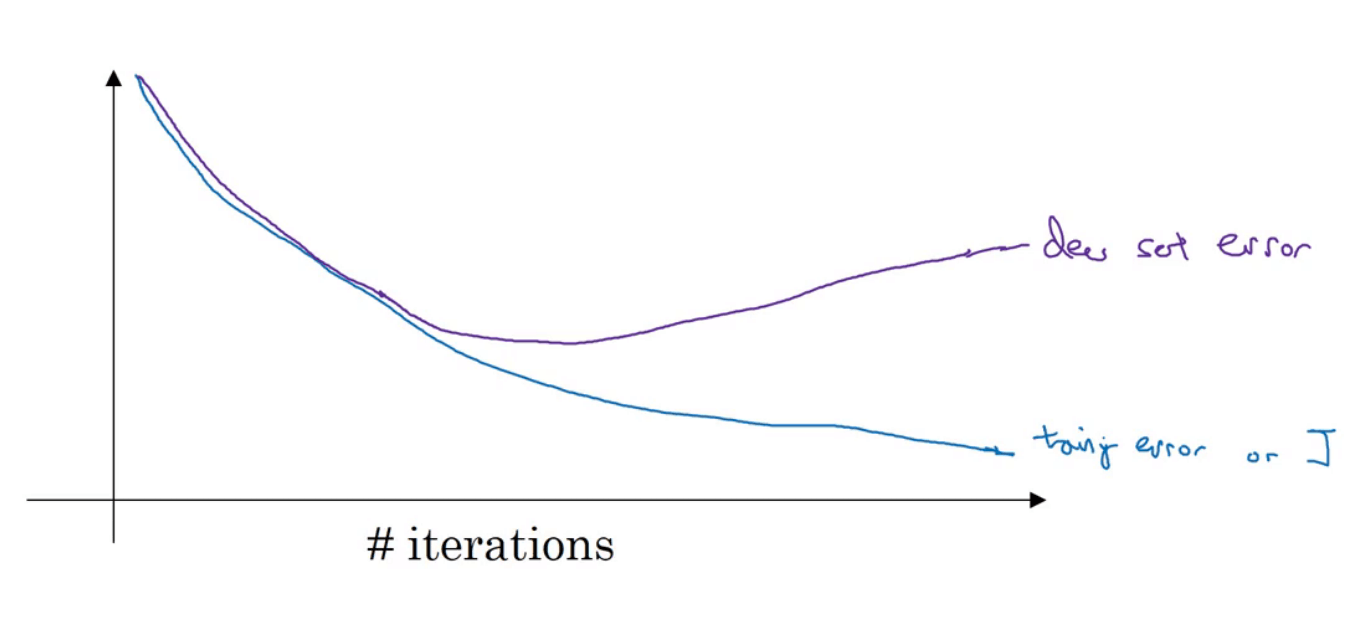
在训练神经网络的过程中,很可能会出现上图中的情况,训练集的cost一直在下降,但是验证集的cost呈先下降后上升的趋势。因此我们就可以在验证集cost曲线的最低点处提前停止训练。