【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.前言
当训练神经网络时,其中一个加速训练的方法就是归一化输入。
2.归一化输入的方法
假设我们有一个训练集,它有两个输入特征。数据集的散点图见下:

归一化输入需要两个步骤:
2.1.零均值化
\[\mu = \frac{1}{m} \sum_{i=1}^m x^{(i)}\] \[x:=x-\mu\]此时,数据集的散点图见下:
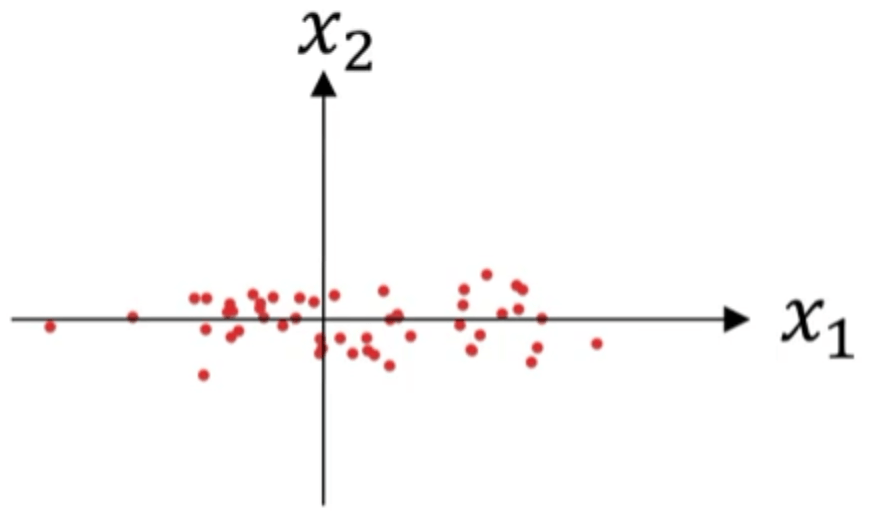
2.2.归一化方差
从2.1部分的图可以看出,特征$x_1$的方差比特征$x_2$的方差要大的多。因此我们第二步对方差进行归一化处理:
\[\sigma^2 = \frac{1}{m} \sum_{i=1}^m [x^{(i)}]^2\] \[x /= \sqrt{\sigma ^2+\epsilon}\]参数$\epsilon$防止除0。
两步都处理完后的数据集散点图见下:
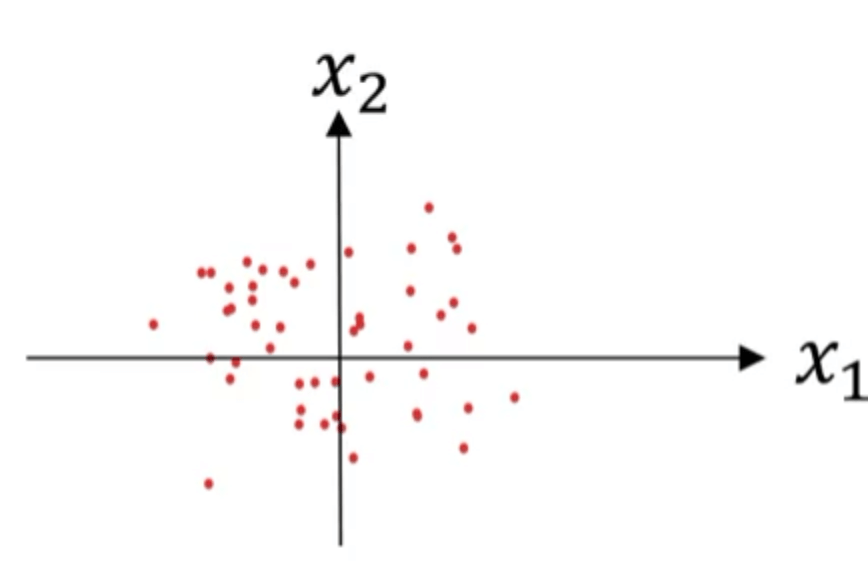
实际上这两个步骤就是将每个特征都转换成了均值为0,方差为1的标准正态分布。
⚠️记得用相同的$\mu$和$\sigma ^2$去归一化测试集,要和训练集保持一致。
3.归一化输入的原因
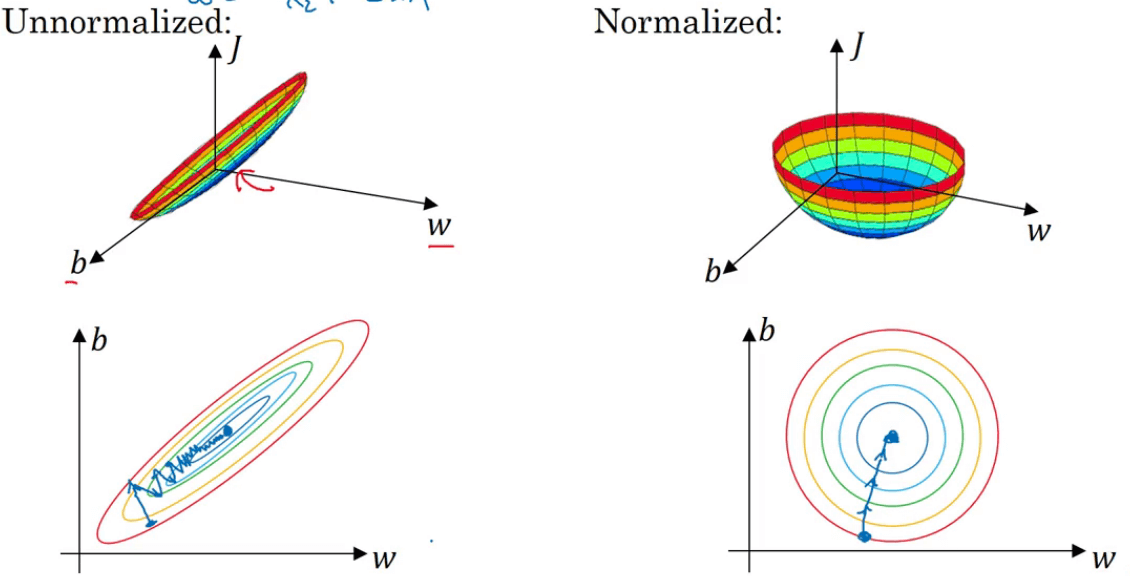
假如数据集有两个特征$x_1$和$x_2$,其中$x_1$的取值范围为1~1000,$x_2$的取值范围为0~1。这会导致$w_1$和$w_2$的差异也非常大。cost function就像是狭长的碗一样(见下图左侧),在这种情况下运行梯度下降法,我们必须要使用一个非常小的学习率,因为如果起点在下图所示位置的话,梯度下降法可能需要多次迭代过程,直到最后找到最小值。
但如果对数据集进行了归一化处理(见下图右侧),梯度下降法无论是从哪个位置开始,都能够更直接地找到最小值。在这种情况下,我们可以使用较大的学习率。
👉如果特征值处于相似范围内(数量级差异并不大),那么归一化输入就显得不是那么重要了。