【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.mini-batch梯度下降法
向量化能让我们有效地对所有m个训练样本进行计算,允许我们处理整个训练集。
例如,训练样本X和训练样本标签Y:
\[X_{(n_x,m)}=[x^{(1)} \ x^{(2)} \ x^{(3)} \ ... \ x^{(m)}]\] \[Y_{(1,m)}=[y^{(1)} \ y^{(2)} \ y^{(3)} \ ... \ y^{(m)}]\]但如果m很大的话,处理速度仍然会很慢。比如,如果m是500万或5000万或者更大的一个数。
在对整个训练集执行梯度下降法时,我们必须处理整个训练集,然后才能进行一步梯度下降法,然后需要再重新处理整个训练集,然后再进行一步梯度下降。如果此时m为500万,这个迭代过程会很慢。
所以如果我们可以在处理完整的500万个样本的训练集之前,先让梯度下降法处理一部分,这样算法的速度就会变快很多。
根据上面的思路,我们把训练集分割为小一点的子训练集,这些子集被取名为mini-batch。假设每个mini-batch中有1000个样本,那么500万个样本一共可划分为5000个mini-batch:$X^{\{1\}},X^{\{2\}},X^{\{3\}},…,X^{\{5000\}}$,对Y进行同样的处理:$Y^{\{1\}},Y^{\{2\}},Y^{\{3\}},…,Y^{\{5000\}}$(注意这里使用大括号表示mini-batch)。
因此,mini-batch的数量t组成了$X^{\{t\}}$和$Y^{\{t\}}$。在本例中,$X^{\{t\}}$的维度为$(n_x,1000)$;$Y^{\{t\}}$的维度为$(1,1000)$。
‼️像我们之前同时处理整个训练集的梯度下降法通常被称为batch梯度下降法。如果每次处理的只是单个mini-batch,则此时的梯度下降法称之为mini-batch梯度下降法。
接下来我们来看下mini-batch梯度下降法的具体流程。还是以上述mini-batch的划分为例:
- for t=1 to 5000
- Forward prop on $X^{\{t\}}$:
- $Z^{[1]}=w^{[1]}X^{\{t\}}+b^{[1]}$
- $A^{[1]}=g^{[1]}(Z^{[1]})$
- ……
- $A^{[L]}=g^{[L]}(Z^{[L]})$
- Compute cost:
- $J^{\{t\}}=\frac{1}{1000} \sum^{1000}_{i=1} L(\hat{y}^{(i)},y^{(i)})+\frac{\lambda}{2*1000} \sum_l \parallel w^{[l]} \parallel ^2_F$
- 注意这里的$\hat{y}^{(i)},y^{(i)}$来自于$X^{\{t\}},Y^{\{t\}}$。
- Backprop to compute gradients with respect to $J^{\{t\}}$ (using ($X^{\{t\}},Y^{\{t\}}$)):
- $w^{[l]}:=w^{[l]}-\alpha dw^{[l]}$
- $b^{[l]}:=b^{[l]}-\alpha db^{[l]}$
- Forward prop on $X^{\{t\}}$:
以上便是每一个mini-batch的训练步骤。和之前介绍的前向传播和反向传播是完全一样的。
‼️对所有训练数据进行一次遍历称之为一个epoch。因此在batch梯度下降法中,一个epoch只能完成一次梯度下降算法。但是如果在mini-batch梯度下降法中,以本例为例,一个epoch可以完成5000次梯度下降算法。
2.深度了解mini-batch梯度下降法
在batch梯度下降法中,每一次迭代将遍历整个训练集,并希望cost function的值随之不断减小,如果某一次迭代cost的值增加了,那么一定是哪里错了,比如学习率太大。
而在mini-batch梯度下降法中,cost并不是单调递减的。因为每次迭代只是对$X^{\{t\}},Y^{\{t\}}$的处理,这就好像每次迭代都使用不同的训练集,所以得到的cost曲线的总体趋势是减小的,但是会有震荡(即噪声)。也就是说其cost并不一定每次迭代都会下降。

2.1.BGD、SGD、MBGD
假设训练集的数据量为m:
- 当mini-batch size=m时,称之为批量梯度下降法(batch gradient descent)。即之前提到的batch梯度下降法,可简称BGD。
- 当mini-batch size=1时,称之为随机梯度下降法(stochastic gradient descent),可简称SGD。
- 当1<mini-batch size<m时,称之为mini-batch梯度下降法(mini-batch gradient descent),可简称MBGD。
通过下图来直观的展示三种梯度下降法在优化cost function时有什么不同:
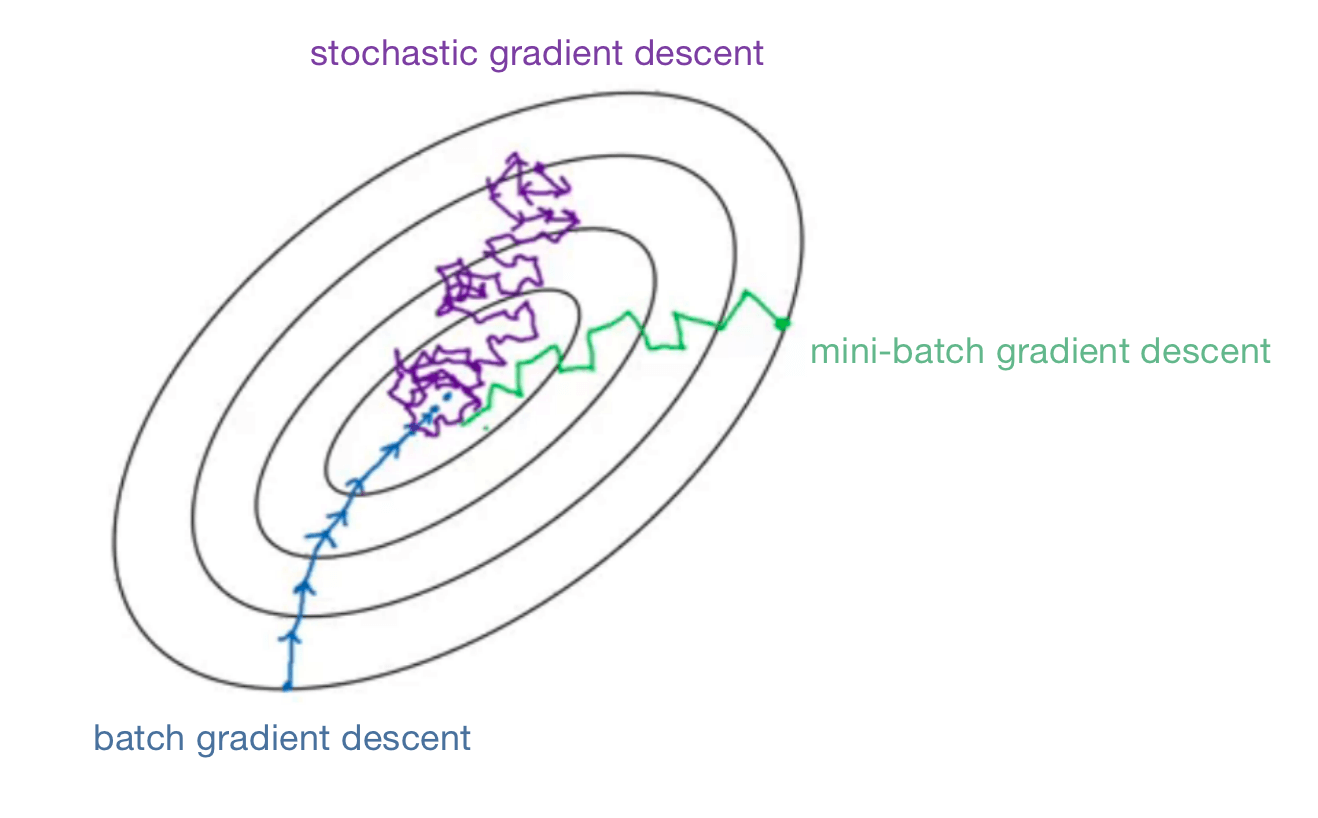
可以看出:
- BGD的噪声相对小些,步长相对大一些。并且最终可以达到最小值。但是每次迭代耗时过长。如果训练集较小,那么BGD是个不错的选择。
- SGD的噪声非常大,并且最后也不会收敛到一个点,一般会在最低点的附近摆动,但是不会到达那里并停在那里。可以通过较小的学习率来降低噪声。SGD最大的缺点之一是失去了利用向量化加速运算的机会,这是非常没有效率的。
- MBGD介于BGD和SGD之间,通常也作为一个更好的选择。适当大小的mini-batch既可以使用向量化加速运算,提高训练效率,并且还不必等待整个训练集都遍历完一遍才运行梯度下降。MBGD并不能保证总是可以达到最小值,但是相比SGD,MBGD的噪声会更小,而且它不会总在最小值附近摆动。如果有什么问题出现,可以尝试慢慢的降低学习率。
2.2.mini-batch size
当训练集的数据量小于2000时,直接使用BGD即可,没必要使用MBGD。
如果训练集的数据量过大,可以尝试使用MBGD。
‼️常用的mini-batch size都是2的幂数,常用的有:64、128、256、512。这是因为计算机内存的布局和访问方式,所以把mini-batch的大小设置为2的幂数时,代码会运行的快一些。
因此我们在第1部分例子中的1000改为1024更为合适,但是mini-batch size=1024还是比较少见的。还是上述提到的值(64、128、256、512)更为常见。
最后还有很重要的一点是,确保每个mini-batch中所有的$X^{\{t\}},Y^{\{t\}}$可以放进你的CPU/GPU内存中。
很显然,mini-batch size也是一个超参数。可以尝试几个不同的2的幂数,然后看能否找到那个让梯度下降法尽可能高效的值。